| Citation: | Qian Yang, Mingkang Ni. ASYMPTOTICS OF A MULTIZONAL INTERNAL LAYER SOLUTION TO A PIECEWISE-SMOOTH SINGULARLY PERTURBED EQUATION WITH A TRIPLE ROOT OF THE DEGENERATE EQUATION[J]. Journal of Applied Analysis & Computation, 2022, 12(6): 2441-2457. doi: 10.11948/20210508 |
ASYMPTOTICS OF A MULTIZONAL INTERNAL LAYER SOLUTION TO A PIECEWISE-SMOOTH SINGULARLY PERTURBED EQUATION WITH A TRIPLE ROOT OF THE DEGENERATE EQUATION
-
Abstract
A singularly perturbed boundary value problem for a stationary equation of reaction-diffusion type in the case when reactive term undergoes discontinuity along some curve that is independent of the small parameter is studied. This is a new class of problems with triple roots of the degenerate equation, which leads to the formation of complex multizonal internal layers in the neighborhood of the discontinuity curve. By the method of asymptotic differential inequalities and matching asymptotic expansion, the existence of a contrast structure solution is proved. Using a different modified boundary layer function method, the asymptotic representation of point itself and this solution are constructed.
-

-
References
[1] V. F. Butuzov and A. I. Bychkov, Asymptotics of the solution of an initial-boundary value problem for a singularly perturbed parabolic equation in the case of double root of the degenerate equation, Differential Equations, 2013, 49(10), 1261–1273. [2] V. F. Butuzov, On the special properties of the boundary layer in singularly perturbed problems with multiple root of the degenerate equation, Mathematical Notes, 2013, 94(1), 60–70. [3] V. F. Butuzov, Singularly perturbed boundary value problem with multizonal interior transitional layer, Automatic Control and Computer Sciences, 2015, 49(7), 493–507. [4] V. F. Butuzov, On periodic solutions to singularly perturbed parabolic problems in the cases of multiple roots of the degenerate equation, Computational Mathematics and Mathematical Physics, 2011, 51(1), 40–50. [5] V. F. Butuzov, N. N. Nefedov, L. Recke and K. R. Schneider, On a singularly perturbed initial value problem in the case of a double root of the degenerate equation, Nonlinear Analysis, 2013, 83, 1–11. [6] V. F. Butuzov, N. N. Nefedov, O. E. Omel'chenko and L. Recke, Partly dissipative system with multizonal initial and boundary layers, Journal of Physics: Conference Series, 2019, 1205, 012009. [7] V. F. Butuzov, On periodic solutions to singularly perturbed parabolic problems in the case of multiple roots of the degenerate equation, Computational Mathematics and Mathematical Physics, 2011, 51(1), 40–50. [8] V. F. Butuzov, Asymptotic behaviour and stability of solutions of a singularly perturbed elliptic problem with a triple root of the degenerate equation, Izvestiya Mathematics, 2017, 81(3), 21–44. [9] A. Dikansky, On stability of nonhomogeneous periodic solutions to reaction-diffusion equations, Nonlinear Analysis: Theory, Methods and Applications, 1997, 30(1), 181–185. [10] A. M. Il'in, Studying singularly perturbed boundary value problems by the method of matching asymptotic expansions, Differentsial'nye Uravneniya, 1985, 21(10), 1760–1766. [11] N. Kopteva and E. O'Riordan, Shishkin meshes in the numerical solution of singularly perturbed differential equations, International Journal of Numerical Analysis and Modeling, 2010, 1(1), 1–18. [12] D. V. Lukyanenko, M. A. Shishlenin and V. T. Volkov, Solving of the coefficient inverse problems for a nonlinear singularly perturbed reaction–diffusion–advection equation with the final time data, Communications in Nonlinear Science and Numerical Simulation, 2018, 54, 233–247. [13] N. T. Levashova, N. N. Nefedov and A. O. Orlov, Time-independent reaction-diffusion equation with a discontinuous reactive term, Computational Mathematics and Mathematical Physics, 2017, 57(5), 854–866. [14] N. T. Levashova, N. N. Nefedov and A. O. Orlov, Asymptotic stability of a stationary solution of a multi-dimensional reaction–diffusion equation with a discontinuous source, Computational Mathematics and Mathematical Physics, 2019, 59(4), 573–582. [15] N. N. Nefedov and M. Ni, Internal layers in the one-dimensional reaction-diffusion equation with a discontinuous reactive term, Computational Mathematics & Mathematical Physics, 2015, 55(12), 2001–2007. [16] M. Ni, Y. Pang, N. T. Levashova and O. A. Nikolaeva, Internal layers for a singularly perturbed second-Order quasilinear differential equation with discontinuous right-hand side, Differential Equations, 2017, 53(12), 1616–1626. [17] M. Ni, Y. Pang and M. A. Davydova, Contrast structures in problems for a stationary equation of reaction-diffusion-advection type with discontinuous nonlinearity, Mathematical Notes, 2018, 104(5), 118–127. [18] G. Nadin, Existence and uniqueness of the solution of a space–time periodic reaction–diffusion equation, Journal of Differential Equations, 2010, 249(6), 1288–1304. [19] N. N. Nefedov and E. I. Nikulin, Existence and stability of periodic solutions for reaction-diffusion equations in the two-dimensional case, Model. Anal. Inform. Syst., 2016, 23 (3), 342–348. [20] M. Ni, X. Qi and N. T. Levashova, Internal layer for a singularly perturbed equation with discontinuous right-hand side, Differential Equations, 2020, 56(10), 1276–1284. [21] N. N. Nefedov and O. V. Rudenko, On front motion in a Burgers-type equation with quadratic and modular nonlinearity and nonlinear amplification, Doklady Mathematics, 2018, 97(1), 99–103. [22] C. V. Pao, Nonlinear Parabolic and Elliptic Equations, New York: Plenum Press, 1992. [23] V. T. Volkov and N. N. Nefedov, Development of the asymptotic method of differential inequalities for investigation of periodic contrast structures in reaction-diffusion equations, Computational Mathematics and Mathematical Physics, 2019, 59(4), 573–582., 2006, 46(4), 585–593. [24] A. B. Vasil'eva and V. F. Butuzov, Asymptotic Methods in Singular Perturbation Theory, Moscow: Vysshaya Shkola, 1990. [25] A. B. Vasil'eva and V. S. Pilyugin, Singularly perturbed boundary value problems with a power-law boundary layer, Ordinary Differential Equations, 2009, 45(3), 323–334. [26] A. B. Vasil'eva, Step-like contrast structures for a singularly perturbed quasilinear second-order differential equation, Zh. Vychisl. Mat. Mat. Fiz., 1995, 35(4), 529–531. [27] Q. Yang and M. Ni, Multizonal internal Layers in the singularly perturbed equation with a discontinuous right-hand side, Computational Mathematics and Mathematical Physics, 2021, 61(6), 953–963. [28] Q. Yang and M. Ni, Asymptotics of the solution to a stationary piecewise-smooth reaction-diffusion equation with a multiple root of the degenerate equation, Science China Mathematics, 2022, 65(2), 291–308. [29] Q. Yang and M. Ni. Asymptotics of the solution to a piecewise-smooth quasilinear second-order differential equation, Journal of Applied Analysis and Computation, 2022, 12(1), 256–269. -
-
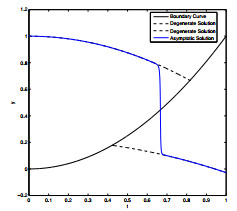
- Figure 1. Zero-order asymptotic solution to problem (4.1).




 DownLoad:
DownLoad: