| Citation: | Zulqurnain Sabir, Muhammad Asif Zahoor Raja, R. Sadat, Khaled. S. Ahmed, Mohamed R. Ali, Wael Al-Kouz. FRACTIONAL MEYER NEURAL NETWORK PROCEDURES OPTIMIZED BY THE GENETIC ALGORITHM TO SOLVE THE BAGLEY-TORVIK MODEL[J]. Journal of Applied Analysis & Computation, 2022, 12(6): 2458-2474. doi: 10.11948/20220019 |
FRACTIONAL MEYER NEURAL NETWORK PROCEDURES OPTIMIZED BY THE GENETIC ALGORITHM TO SOLVE THE BAGLEY-TORVIK MODEL
-
Abstract
The current investigations are related to indicate a competent numerical fractional Meyer neural network (FMNN) procedure using the optimization of genetic algorithm and interior-point algorithm (GAIPA), i.e., FMNN-GAIPA for solving the Bagley--Torvik model (BTM). A merit function based on the differential BTM form, and its corresponding initial conditions is constructed and then optimized with the FMNN-GAIPA. Three different BTM cases will be solved through the FMNN-GAIPA and the correctness of the proposed FMNN-GAIPA is observed by using the comparison for each case of the BTM with the exact solutions. The statistical investigations based on the appropriate large independent trials recognized the constancy of the FMNN-GAIPA in terms of robustness, convergence, and stability trials. In addition, the annotations over the statistical measures validate the values of FMNN-GAIPA.
-

-
References
[1] A. Arikoglu, et al., Solution of fractional differential equations by using differential transform method, Chaos, Solitons & Fractals, 2007, 34(5), 1473–1481. [2] M. A. Abdelkawy, et al., Numerical investigations of a new singular second-order nonlinear coupled functional Lane–Emden model, Open Physics, 2020, 18(1), 770–778. [3] A. N. Akkilic, Z. Sabir, M. A. Z. Raja and H. Bulut, Numerical treatment on the new fractional-order SIDARTHE COVID-19 pandemic differential model via neural networks, The European Physical Journal Plus, 2022, 137(3), 1–14. [4] M. Artar, et al., Optimum weight design of steel space frames with semi-rigid connections using harmony search and genetic algorithms, Neural Computing and Applications, 2018, 29(11), 1089–1100. [5] J. M. Adánez, et al., Multidimensional membership functions in T-S fuzzy models for modelling and identification of nonlinear multivariable systems using genetic algorithms, Applied Soft Computing, 2019, 75, 607–615. doi: 10.1016/j.asoc.2018.11.034 [6] K. S. Al-Ghafri and H. Rezazadeh, Solitons and other solutions of (3+1)-dimensional space-time fractional modified KdV-Zakharov-Kuznetsov equation, Applied Mathematics and Nonlinear Sciences, 2019, 4(2), 289–304. [7] Al-Mdallal, et al., A collocation-shooting method for solving fractional boundary value problems, Communications in Nonlinear Science and Numerical Simulation, 2010, 15(12), 3814–3822. [8] A. Ayub, et al., Nanoscale heat and mass transport of magnetized 3-D chemically radiative hybrid nanofluid with orthogonal/inclined magnetic field along rotating sheet, Case Studies in Thermal Engineering, 2021, 26, 101193. [9] D. W. Brzeziński, Review of numerical methods for NumILPT with computational accuracy assessment for fractional calculus, Applied Mathematics and Nonlinear Sciences, 2018, 3(2), 487–502. [10] R. L. Bagley, et al., Fractional calculus-a different approach to the analysis of viscoelastically damped structures, AIAA journal, 1983, 21(5), 741–748. [11] R. L. Bagley, et al., Fractional calculus in the transient analysis of viscoelastically damped structures, AIAA journal, 1985, 23(6), 918–925. [12] R. L. Bagley and P. J. Torvik, On the fractional calculus model of viscoelastic behavior, Journal of Rheology, 1986, 30(1), 133–155. [13] J. Bleyer, Advances in the simulation of viscoplastic fluid flows using interior-point methods, Computer Methods in Applied Mechanics and Engineering, 2018, 330, 368–394. [14] S. Breedveld, et al., An interior-point implementation developed and tuned for radiation therapy treatment planning, Computational Optimization and Applications, 2017, 68(2), 209–242. [15] H. M. Baskonus, H. Bulut, and T. A. Sulaiman, New complex hyperbolic structures to the lonngren-wave equation by using sine-gordon expansion method, Applied Mathematics and Nonlinear Sciences, 2019, 4(1), 129–138. [16] Y. Çenesiz, et al., The solution of the Bagley–Torvik equation with the generalized Taylor collocation method, Journal of the Franklin institute, 2010, 347(2), 452–466. [17] K. Diethelm, et al., Numerical solution of the Bagley-Torvik equation, BIT Numerical Mathematics, 2002, 42(3), 490–507. [18] M. Dewasurendra and K. Vajravelu, On the method of inverse mapping for solutions of coupled systems of nonlinear differential equations arising in nanofluid flow, heat and mass transfer, Applied Mathematics and Nonlinear Sciences, 2018, 3(1), 1–14. [19] E. İ. Eskitaşçıoğlu, M. B. Aktaş and H. M. Baskonus, New complex and hyperbolic forms for Ablowitz-Kaup-Newell-Segur wave equation with fourth order, Applied Mathematics and Nonlinear Sciences, 2019, 4(1), 93–100. [20] El-Sayed, et al., Analytical and numerical solutions of multi-term nonlinear fractional orders differential equations, Applied Numerical Mathematics, 2010, 60(8), 788–797. [21] C. A. C. Flórez, et al., Control structure for a car-like robot using artificial neural networks and genetic algorithms, Neural Computing and Applications, 2018, 1–14. [22] A. Ghorbani, et al., Application of He's Variational Iteration Method to Solve Semidifferential Equations of ðth Order, Mathematical Problems in Engineering, 2008, 2008, 1–9. [23] Y. Guerrero-Sánchez, et al., Solving a class of biological HIV infection model of latently infected cells using heuristic approach, Discrete & Continuous Dynamical Systems-S, 2021, 14(10), 3611. [24] S. Goyal, P. Garg and V. N. Mishra, New composition of graphs and their Wiener indices, Applied Mathematics and Nonlinear Sciences, 2019, 4(1), 163–168. [25] Y. Hu, et al., Analytical solution of the linear fractional differential equation by Adomian decomposition method, Journal of Computational and Applied Mathematics, 2008, 215(1), 220–229. [26] S. Kazem, An integral operational matrix based on Jacobi polynomials for solving fractional-order differential equations, Applied Mathematical Modelling, 2013, 37(3), 1126–1136. [27] C. M. Khalique and I. E. Mhlanga, Travelling waves and conservation laws of a (2+ 1)-dimensional coupling system with Korteweg-de Vries equation, Applied Mathematics and Nonlinear Sciences, 2018, 3(1), 241–254. [28] Y. Li, et al., Haar wavelet operational matrix of fractional order integration and its applications in solving the fractional order differential equations, Applied mathematics and computation, 2010, 216(8), 2276–2285. [29] C. Liu, A new infeasible-interior-point algorithm for linear programming over symmetric cones, Acta Mathematicae Applicatae Sinica, English Series, 2017, 33(3), 771–788. [30] I. Podlubny, et al., Matrix approach to discretization of fractional derivatives and to solution of fractional differential equations and their systems, In 2009 IEEE Conference on Emerging Technologies & Factory Automation, September 2009, 1–6. [31] I. Podlubny, Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications, Elsevier, 1998. [32] M. A. Z. Raja, et al., Design of unsupervised fractional neural network model optimized with interior point algorithm for solving Bagley–Torvik equation, Mathematics and Computers in Simulation, 2017, 132, 139–158. [33] S. S. Ray, On Haar wavelet operational matrix of general order and its application for the numerical solution of fractional Bagley Torvik equation, Applied Mathematics and Computation, 2012, 218(9), 5239–5248. [34] M. A. Z. Raja, et al., Numerical solution of doubly singular nonlinear systems using neural networks-based integrated intelligent computing, Neural Computing and Applications, 2019, 31(3), 793–812. [35] M. A. Z. Raja, M. Umar, Z. Sabir, J. A. Khan and D. Baleanu, A new stochastic computing paradigm for the dynamics of nonlinear singular heat conduction model of the human head, The European Physical Journal Plus, 2018, 133(9), 1–21. [36] Z. Sabir, et al., Applications of Gudermannian neural network for solving the SITR fractal system, Fractals, doi: 10.1142/S0218348X21502509. [37] Z. Sabir, et al., Design of Morlet wavelet neural network for solving the higher order singular nonlinear differential equations, Alexandria Engineering Journal, 2021, 60(6), 5935–5947. [38] Z. Sabir, et al., Solution of novel multi-fractional multi-singular Lane–Emden model using the designed FMNEICS, Neural Computing and Applications, 2021, 1–16. [39] Z. Sabir, et al., Fractional Meyer Neuro-swarm heuristic solver for multi-fractional Order doubly singular model based on Lane-Emden equation, Fractals, 2021, 29(5), 2140017–1219. [40] Z. Sabir, et al., Stochastic numerical approach for solving second order nonlinear singular functional differential equation, Applied Mathematics and Computation, 2019, 363, 124605. [41] Z. Sabir, et al., A neuro-swarming intelligence-based computing for second order singular periodic non-linear boundary value problems, Frontiers in Physics, 2020, 8, 224. [42] Z. Sabir, et al., Evolutionary computing for nonlinear singular boundary value problems using neural network, genetic algorithm and active-set algorithm, The European Physical Journal Plus, 2021, 136(2), 1–19. [43] Z. Sabir, et al., Intelligence computing approach for solving second order system of Emden–Fowler model, Journal of Intelligent & Fuzzy Systems, 2020, 38(6), 7391–7406. [44] Z. Sabir, et al., Solving a novel designed second order nonlinear Lane-Emden delay differential model using the heuristic techniques, Applied Soft Computing, 2021, 102, 107105. [45] Z. Sabir, T. Botmart, M. A. Z. Raja and W. Weera, An advanced computing scheme for the numerical investigations of an infection-based fractional-order nonlinear prey-predator system, Plus one, 2022, 17(3), e0265064. [46] Z. Sabir, et al., A novel design of fractional Meyer wavelet neural networks with application to the nonlinear singular fractional Lane-Emden systems, Alexandria Engineering Journal, 2021, 60(2), 2641–2659. [47] Z. Sabir, M. A. Z. Raja, M. Umar, M. Shoaib and D. Baleanu, FMNSICS: Fractional Meyer neuro-swarm intelligent computing solver for nonlinear fractional Lane–Emden systems, Neural Computing and Applications, 2022, 34(6), 4193–4206. [48] Z. Sabir, M. A. Z. Raja, T. G. Nguyen, I. Fathurrochman, R. Sadat and M. R. Ali, Applications of neural networks for the novel designed of nonlinear fractional seventh order singular system, The European Physical Journal Special Topics, 2022, 1–15. [49] Z. Sabir, Design of stochastic numerical solver for the solution of singular three-point second-order boundary value problems, Neural Computing and Applications, 2021, 33(7), 2427–2443. [50] T. Sajid, et al., Impact of activation energy and temperature-dependent heat source/sink on Maxwell-Sutterby fluid, Mathematical Problems in Engineering, 2020. [51] T. Sajid, et al., Upshot of radiative rotating Prandtl fluid flow over a slippery surface embedded with variable species diffusivity and multiple convective boundary conditions, Heat Transfer, 2021, 50(3), 2874–2894. [52] P. J. Torvik, et al., On the appearance of the fractional derivative in the behavior of real materials, 1984. [53] M. Umar, Z. Sabir, M. A. Z. Raja, M. Shoaib, M. Gupta and Y. G. Sánchez, A stochastic intelligent computing with neuro-evolution heuristics for nonlinear SITR system of novel COVID-19 dynamics, Symmetry, 2020, 12(10), 1628. [54] M. Umar, Z. Sabir, M. A. Z. Raja, F. Amin, T. Saeed and Y. Guerrero-Sanchez, Integrated neuro-swarm heuristic with interior-point for nonlinear SITR model for dynamics of novel COVID-19, Alexandria Engineering Journal, 2021, 60(3), 2811–2824. [55] M. Umar, et al., A novel study of Morlet neural networks to solve the nonlinear HIV infection system of latently infected cells, Results in Physics, 2021, 25, 104235. [56] J. Umenberger, Specialized interior-point algorithm for stable nonlinear system identification, IEEE Transactions on Automatic Control, 2018, 64(6), 2442–2456. [57] M. Umar, et al, Numerical treatment for the three-dimensional eyring-powell fluid flow over a stretching sheet with velocity slip and activation energy, Advances in Mathematical Physics, 2019, 2019. [58] A. Yokuş and S. Gülbahar, Numerical solutions with linearization techniques of the fractional Harry Dym equation, Applied Mathematics and Nonlinear Sciences, 2019, 4(1), 35–42. [59] A. Zanelli, et al., FORCES NLP: an efficient implementation of interior-point methods for multistage nonlinear nonconvex programs, International Journal of Control, 2020, 93(1), 13–29. [60] A. Zameer, et al., Bio-inspired heuristics for layer thickness optimization in multilayer piezoelectric transducer for broadband structures, Soft Computing, 2019, 23(10), 3449–3463. -
-
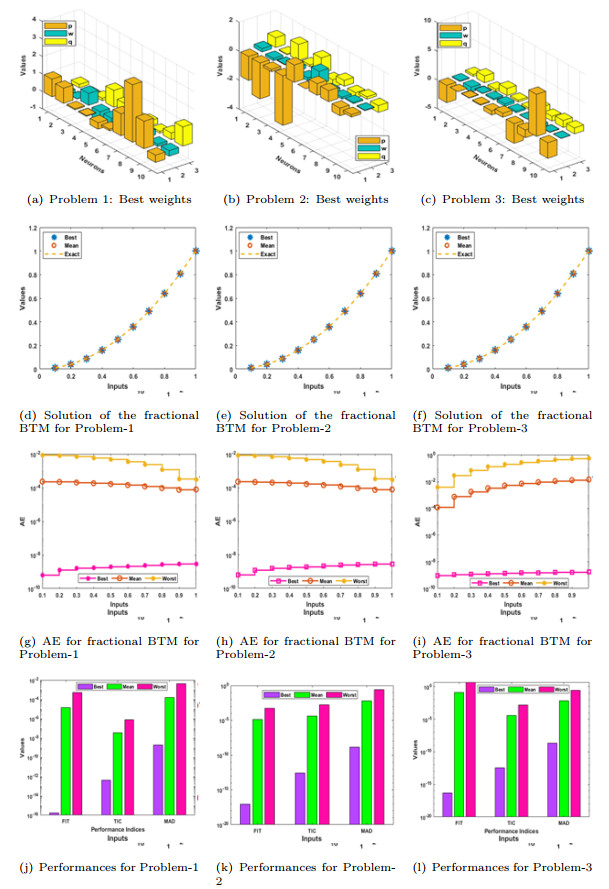
- Figure 1. Results plots, weights, AE and performance for the fractional BTM
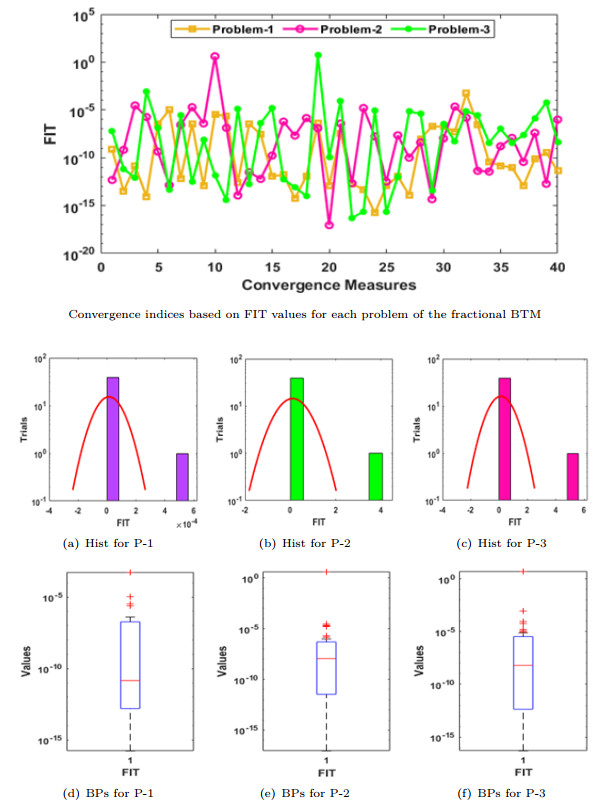
- Figure 2. Statistical performances-based FIT for the fractional BTM with hist and boxplots
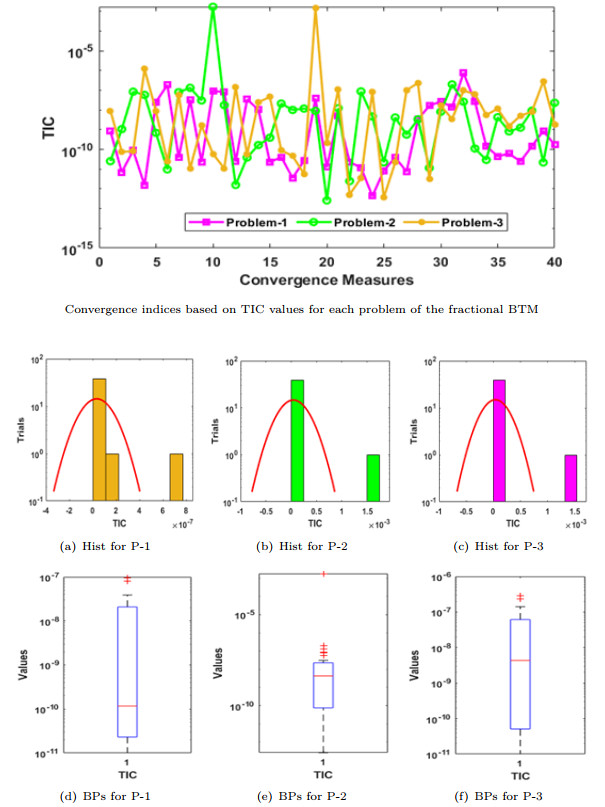
- Figure 3. Statistical performances-based TIC for the fractional BTM with hist and boxplots
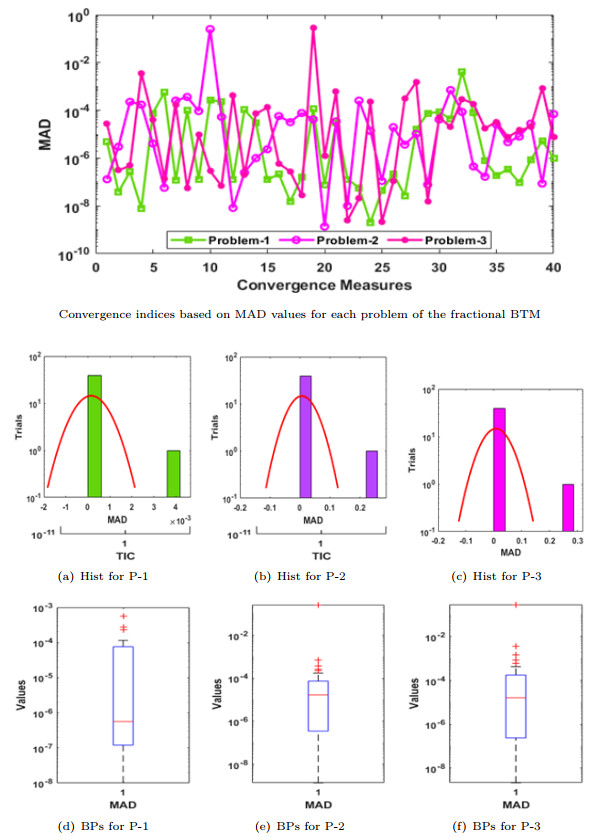
- Figure 4. Statistical performances-based MAD for the fractional BTM with hist and boxplots




 DownLoad:
DownLoad: