| Citation: | Diandian Tang, Jingli Ren. FLIP BIFURCATION WITH RANDOM EXCITATION[J]. Journal of Applied Analysis & Computation, 2022, 12(6): 2488-2510. doi: 10.11948/20220042 |
FLIP BIFURCATION WITH RANDOM EXCITATION
-
Abstract
In this paper, flip bifurcation with random excitation is studied by employing the methods of normal forms, Picard iterations and orthogonal polynomial approximation. For the codimension one case, a Neimark-Sacker bifurcation, a 1:2 resonance and a fold-flip bifurcation are detected. It is found that the system undergoes heteroclinic bifurcation and homoclinic bifurcation near 1:2 resonance point, a hopf bifurcation and a cusp bifurcation near fold-flip bifurcation point. For the codimension two case, the system undergoes only a flip bifurcation when random excitation is imposed on the nonlinear term. In addition, numerical simulations are given to show the disparity between the codimension one and two cases.
-

-
References
[1] Ashish and J. Cao, A novel fixed point feedback approach studying the dynamical behaviors of standard logistic map, Int. J. Bifurcat. Chaos, 2019, 29(1), 1950010. [2] Ashish, J. Cao and F. Alsaadi, Chaotic evolution of difference equation in mann orbit, J. Appl. Anal. Comput., 2021, 11(6), 3063-3082. [3] Ashish, J. Cao and R. Chugh, Chaotic behavior of logistic map in superior orbit and an improved chaos-based traffic control model, Nonlinear Dyn., 2018, 94(2), 959-975. doi: 10.1007/s11071-018-4403-y [4] F. Balibrea, H. Oliveira and J. Valverde, Topological equivalences for one-parameter bifurcations of scalar maps, J. Nonlinear Sci., 2017, 27(2), 661-685. doi: 10.1007/s00332-016-9347-0 [5] P. Borwein and T. Erdélyi, Polynomials and Polynomial Inequalities, Springer, New York, 1995. [6] P. Collet, J. Eckmann and H. Koch, Period doubling bifurcations for families of maps on $\mathbb{R}^n$, J. Stat. Phys., 1981, 25(1), 1-14. [7] J. Eckmann, H. Koch and P. Wittwer, Existence of a fixed point of the doubling transformation for area-preserving maps of the plane, Phys. Rev. A, 1982, 26(1), 720-722. [8] A. Giraldo, B. Krauskopf and H. Osinga, Cascades of global bifurcations and chaos near a homoclinic flip bifurcation: a case study, SIAM J. Appl. Dyn. Syst., 2018, 17(4), 2784-2829. doi: 10.1137/17M1149675 [9] M. He, S. Tang, G. Tang et al., Bifurcation analysis of an ecological system with state-dependent feedback control and periodic forcing, Int. J. Bifurcat. Chaos, 2021, 31(15), 2150227. doi: 10.1142/S0218127421502278 [10] J. Huang, S. Liu, S. Ruan et al., Bifurcations in a discrete predator-prey model with nonmonotonic functional response, J. Math. Anal. Appl., 2018, 464(1), 201-230. doi: 10.1016/j.jmaa.2018.03.074 [11] Y. Kuznetsov, Elements of Applied Bifurcation Theory, Springer, New York, 1995. [12] Y. Kuznetsov, H. Meijer and L. Veen, The fold-flip bifurcation, Int. J. Bifurcat. Chaos, 2004, 14(7), 2253-2282. [13] S. Li and W. Zhang, Bifurcations of a discrete prey-predator model with Holling type Ⅱ functional response, Discrete Contin. Dyn. Sys. Ser. B, 2010, 14(1), 159-176. [14] X. Li and J. Ren, Periodic perturbation of a cusp bifurcation, Sci. China Math., 2020, 50(2), 269-286. [15] R. Ma, Y. Bai and F. Wang, Dyanmical behavior analysis of a two-dimensional discrete predator-prey model with refuge and fear, J. Appl. Anal. Comput., 2020, 10(4), 1683-1697. [16] S. Ma, W. Xu and T. Fang, Analysis of period-doubling bifurcation in double-well stochastic Duffing system via Laguerre polynomial approximation, Nonlinear Dyn., 2008, 52(3), 289-299. [17] G. Neverova and E. Frisman, Dynamic modes of population size and its genetic structure for species with nonoverlapping generations and stage development, Commun. Nonlinear Sci., 2021, 94, 105554. [18] A. Nikiforov, V. Uvarov and S. Suslov, Classical Orthogonal Polynomials of a Discrete Variable, Springer, Berlin, 1991. [19] A. Quarteroni, R. Sacco and F. Saleri, Orthogonal Polynomials in Approximation Theory, Springer, New York, 2000. [20] J. Ren and L. Yu, Codimension-two bifurcation, chaos and control in a discrete-time information diffusion model, J. Nonlinear Sci., 2016, 26(6), 1895-1931. [21] W. Sayed, A. Radwan and H. Fahmy, Design of positive, negative, and alternating sign generalized logistic maps, Discrete Dyn. Nat. Soc., 2015, 2015, 586783. [22] S. Suslov, Classical orthogonal polynomials of a discrete variable, Lett. Math. Phys., 1987, 14(1), 77-88. [23] A. Taylor and D. Lay, Introduction to Functional Analysis, Wiley, New York, 1980. [24] A. Vanderbauwhede, Centre Manifolds, Normal Forms and Elementary Bifurcations, In: U. Kirchgraber and H. Walther (Eds), Dynamics Reported, Vieweg&Teubner Verlag, Wiesbaden, 1989, 2, 57-68. [25] L. Zhang and C. Zhang, Codimension one and two bifurcations of a discrete stage-structured population model with self-limitation, J. Differ. Equ. Appl., 2018, 24(8), 1210-1246. [26] J. Zhong and X. Zhou, Codimension-3 flip bifurcation of a class of difference equations, Int. J. Bifurcat. Chaos, 2018, 28(7), 1850090. -
-
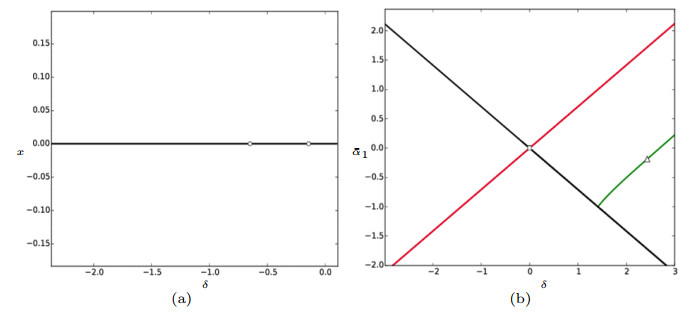
- Figure 1. The bifurcation diagrams for system (3.10).
-
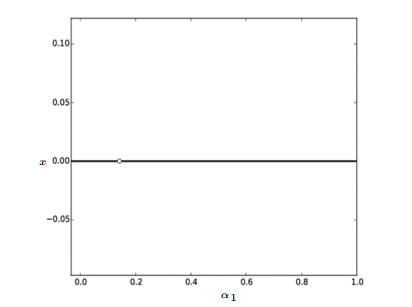
Figure 2. The bifurcation diagrams for system (4.2) with
$ x=x_{0}(n) $ . -
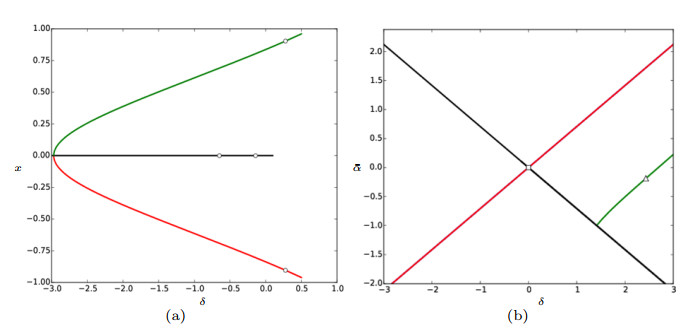
Figure 3. The bifurcation diagram for system (4.3) with
$ x=x_{0}(n) $ . There is only one flip bifurcation at the origin when$ \delta=-0.2 $ ,$ \alpha_1=0.14 $ and$ \bar{\alpha}_2=0.1 $ .




 DownLoad:
DownLoad: