| Citation: |
Yingxian Zhu, Shuangfei Li, Yunxian Dai. STABILITY ANALYSIS OF A FRACTIONAL PREDATOR-PREY SYSTEM WITH TWO DELAYS AND INCOMMENSURATE ORDERS[J]. Journal of Applied Analysis & Computation, 2022, 12(3): 981-1006. doi: 10.11948/20220093
|
STABILITY ANALYSIS OF A FRACTIONAL PREDATOR-PREY SYSTEM WITH TWO DELAYS AND INCOMMENSURATE ORDERS
-
Abstract
In this paper, we consider a fractional predator-prey system with two delays and incommensurate orders. Firstly, the local stability of positive equilibrium of the system without delay is discussed. Secondly, we calculate the critical value of Hopf bifurcation by taking one delay as bifurcation parameter. Then, as two nonidentical delays change simultaneously, the stability switching curves, the directions of crossing and the existence of Hopf bifurcation are obtained. Finally, numerical simulations are presented to verify the given theoretical results.
-
-
References
[1] M. Agarwal and R. Pathak, Harvesting and Hopf Bifurcation in a prey-predator model with Holling Type Ⅳ Functional Response, Int. J. Math. Soft Comput., 2012, 2(1), 83-92. doi: 10.26708/IJMSC.2012.1.2.10 [2] J. Alidousti and M. M. Ghahfarokhi, Stability and bifurcation for time delay fractional predator-prey system by incorporating the dispersal of prey, Appl. Math. Model., 2019, 72, 385-402. doi: 10.1016/j.apm.2019.03.029 [3] M. Banerjee and E. Venturino, A phytoplankton-toxic phytoplankton-zooplankton model, Ecol. Complex., 2011, 8(3), 239-248. doi: 10.1016/j.ecocom.2011.04.001 [4] L. Chang, G. Sun, Z. Wang and Z. Jin, Rich dynamics in a spatial predator–prey model with delay, Appl. Math. Comput., 2015, 256, 540-550. [5] D. Copot, R. De Keyser, E. Derom, M. Ortigueira and M. Ionescu Clara, Reducing bias in fractional order impedance estimation for lung function evaluation, Biomed. Signal Proces. Control, 2018, 39, 74-80. doi: 10.1016/j.bspc.2017.07.009 [6] W. Deng, C. Li and J. Lü, Stability analysis of linear fractional differential system with multiple time delays, Nonlinear Dyn., 2007, 48(4), 409-416. doi: 10.1007/s11071-006-9094-0 [7] E. H. Doha, A. H. Bhrawy and S. S. Ezz-Eldien, A new Jacobi operational matrix: an application for solving fractional differential equations, Appl. Math. Model., 2012, 36(10), 4931-4943. doi: 10.1016/j.apm.2011.12.031 [8] G. S. Frederico and D. F. Torres, Fractional conservation laws in optimal control theory, Nonlinear Dyn., 2008, 53(3), 215-222. doi: 10.1007/s11071-007-9309-z [9] S. Gakkhar, K. Negi and S. K. Sahani, Effects of seasonal growth on ratio dependent delayed prey predator system, Commun. Nonlinear Sci. Numer. Simul., 2009, 14(3), 850-862. doi: 10.1016/j.cnsns.2007.10.013 [10] K. Gu, S. I. Niculescu and J. Chen, On stability crossing curves for general systems with two delays, J. Math. Anal. Appl., 2005, 311(1), 231-253. doi: 10.1016/j.jmaa.2005.02.034 [11] L. Guerrini, A. Matsumoto and F. Szidarovszky, Delay Cournot duopoly models revisited, Chaos, 2018, 28(9), 093113. doi: 10.1063/1.5020903 [12] R. Hilfer, Applications of fractional calculus in physics, World Scientific, Singapore, 2000. [13] C. Huang, X. Zhao, X. Wang, Z. Wang, M. Xiao and J. Cao, Disparate delays-induced bifurcations in a fractional-order neural network, J. Frankl. Inst. Eng. Appl. Math., 2019, 356(5), 2825-2846. doi: 10.1016/j.jfranklin.2018.11.027 [14] T. K. Kar and A. Ghorai, Dynamic behaviour of a delayed predator–prey model with harvesting, Appl. Math. Comput., 2011, 217(22), 9085-9104. [15] N. Laskin, Fractional quantum mechanics, Phys. Rev. E, 2000, 62(3), 3135-3145. doi: 10.1103/PhysRevE.62.3135 [16] X. Lin and H. Wang, Stability analysis of delay differential equations with two discrete delays, Can. Appl. Math. Q., 2012, 20(4), 519-533. [17] X. Liu and H. Fang, Periodic pulse control of Hopf bifurcation in a fractional-order delay predator-prey model incorporating a prey refuge, Adv. Differ. Equ., 2019, 2019(1), 1-30. doi: 10.1186/s13662-018-1939-6 [18] B. B. Mandelbrot, The fractal geometry of nature, WH freeman, New York, 1982. [19] D. Matignon, Stability results for fractional differential equations with applications to control processing, Computational Engineering in Systems Applications, 1996, 2(1), 963-968. [20] A. Matsumoto and F. Szidarovszky, Nonlinear Cournot duopoly with implementation delays, Chaos Solitons Fractals, 2015, 79, 157-165. doi: 10.1016/j.chaos.2015.05.010 [21] C. I. Muresan, C. Ionescu, S. Folea and R. De Keyser, Fractional order control of unstable processes: the magnetic levitation study case, Nonlinear Dyn., 2015, 80(4), 1761-1772. doi: 10.1007/s11071-014-1335-z [22] M. D. Ortigueira, Fractional calculus for scientists and engineers, Springer Science & Business Media, Berlin, Heidelberg, 2011. [23] N. Pecora and M. Sodini, A heterogenous Cournot duopoly with delay dynamics: Hopf bifurcations and stability switching curves, Commun. Nonlinear Sci. Numer. Simul., 2018, 58, 36-46. doi: 10.1016/j.cnsns.2017.06.015 [24] I. Podlubny, Fractional differential equations, Academic Press, New York, 1999. [25] F. A. Rihan, S. Lakshmanan, A. H. Hashish, R. Rakkiyappan and E. Ahmed, Fractional-order delayed predator-prey systems with Holling type-Ⅱ functional response, Nonlinear Dyn., 2015, 80(1), 777-789. [26] A. Singh, A. Parwaliya and A. Kumar, Hopf bifurcation and global stability of density-dependent model with discrete delays involving Beddington-DeAngelis functional response, Math. Meth. Appl. Sci., 2021, 44(11), 8838-8861. doi: 10.1002/mma.7311 [27] P. Song, H. Zhao and X. Zhang, Dynamic analysis of a fractional order delayed predator-prey system with harvesting, Theory Biosci., 2016, 135(1), 59-72. [28] S. Wang, H. Tang and Z. Ma, Hopf bifurcation of a multiple-delayed predator-prey system with habitat complexity, Math. Comput. Simul., 2021, 180, 1-23. doi: 10.1016/j.matcom.2020.08.008 [29] C. Xu, X. Tang, M. Liao and X. He, Bifurcation analysis in a delayed Lokta–Volterra predator–prey model with two delays, Nonlinear Dyn., 2011, 66(1), 169-183. [30] C. Xu, M. Liao, P. Li, Y. Guo and Z. Liu, Bifurcation properties for fractional order delayed BAM neural networks, Cogn. Comput., 2021, 13(2), 322-356. doi: 10.1007/s12559-020-09782-w [31] J. Yuan, L. Zhao, C. Huang and M. Xiao, Stability and bifurcation analysis of a fractional predator-prey model involving two nonidentical delays, Math. Comput. Simul., 2021, 181, 562-580. doi: 10.1016/j.matcom.2020.10.013 [32] L. Zhao, C. Huang and J. Cao, Dynamics of fractional-order predator-prey model incorporating two delays, Fractals-Complex Geom. Patterns Scaling Nat. Soc., 2021, 29(01), 2150014. -
-
Figures(12)
Export File
Citation
Yingxian Zhu, Shuangfei Li, Yunxian Dai. STABILITY ANALYSIS OF A FRACTIONAL PREDATOR-PREY SYSTEM WITH TWO DELAYS AND INCOMMENSURATE ORDERS[J]. Journal of Applied Analysis & Computation, 2022, 12(3): 981-1006. doi: 10.11948/20220093
Format
Content
DownLoad:
-
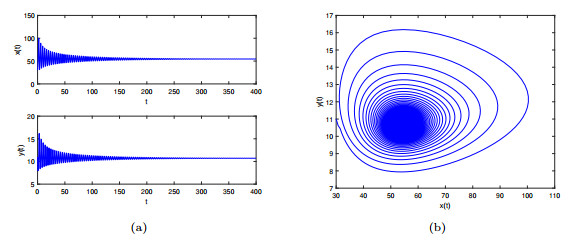
Figure 1. The positive equilibrium
$ J^{*} $ of system$ (4.1) $ is locally asymptotically stable when$ \tau_{1}=0 $ and$ \tau_{2}=0 $ with$ \gamma_{1}=0.9 $ and$ \gamma_{2}=0.95 $ . -
Figure 2. The positive equilibrium
$ J^{*} $ of system$ (4.1) $ is locally asymptotically stable when$ \tau_{1}=0.8<\tau_{10} $ and$ \tau_{2}=0 $ with$ \gamma_{1}=0.9 $ and$ \gamma_{2}=0.95 $ . -
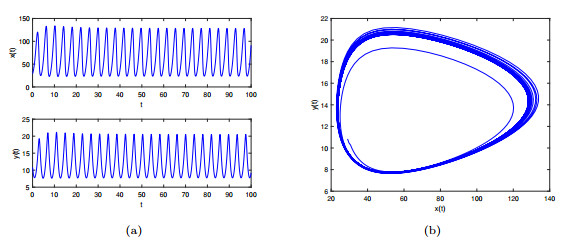
Figure 3. The system
$ (4.1) $ appears Hopf bifurcation when$ \tau_{1}=1>\tau_{10} $ and$ \tau_{2}=0 $ with$ \gamma_{1}=0.9 $ and$ \gamma_{2}=0.95 $ . -
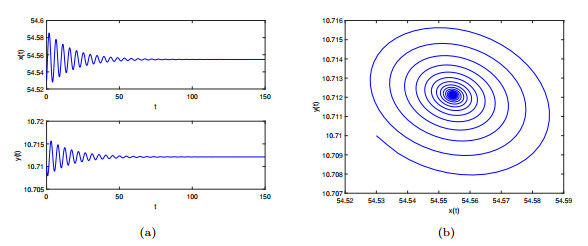
Figure 4. The positive equilibrium
$ J^{*} $ of system$ (4.1) $ is locally asymptotically stable when$ \tau_{1}=0 $ with$ \tau_{2}=0.2<\tau_{20} $ with$ \gamma_{1}=0.9 $ and$ \gamma_{2}=0.95 $ . -
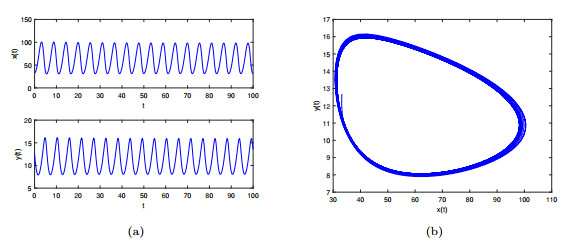
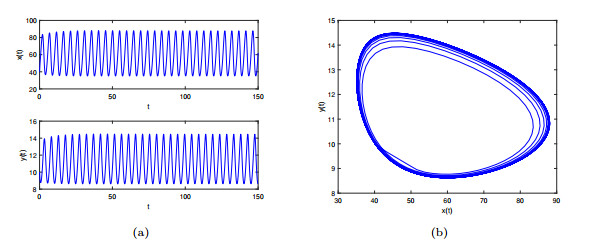
Figure 5. The system
$ (4.1) $ appears Hopf bifurcation when$ \tau_{1}=0 $ and$ \tau_{2}=0.35>\tau_{20} $ with$ \gamma_{1}=0.9 $ and$ \gamma_{2}=0.95 $ . -
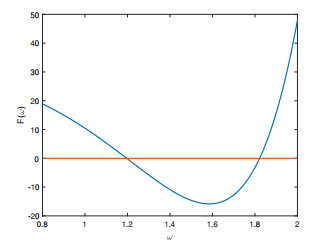
Figure 6. Graph of F(
$ \omega $ ) when$ \gamma_{1}=0.9 $ and$ \gamma_{2}=0.95 $ . -
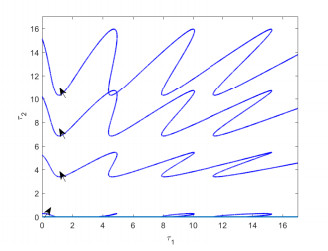
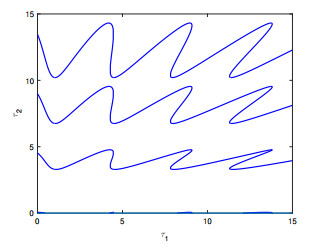
Figure 7. Plot of the stability switching curves when
$ \gamma_{1}=0.9 $ and$ \gamma_{2}=0.95 $ . -
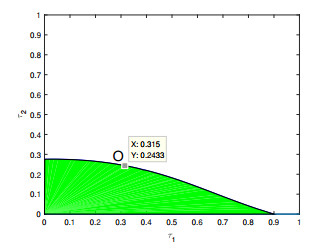
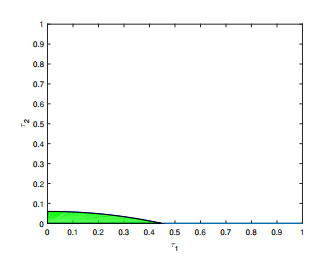
Figure 8. The stable region of system
$ (4.1) $ with$ \gamma_{1}=0.9 $ and$ \gamma_{2}=0.95 $ . -
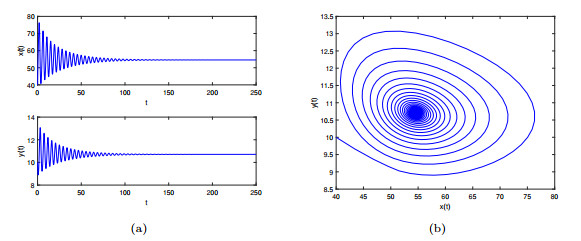
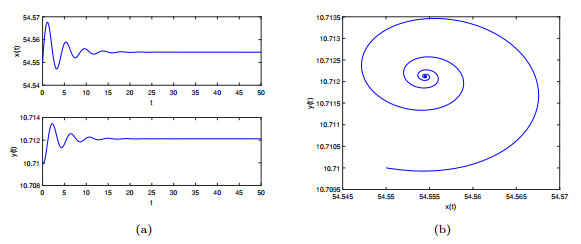
Figure 9. The positive equilibrium
$ J^{*} $ of system$ (4.1) $ is locally asymptotically stable when$ \tau_{1}=0.315 $ and$ \tau_{2}=0.24<0.2433 $ with$ \gamma_{1}=0.9 $ and$ \gamma_{2}=0.95 $ . -
Figure 10. The system
$ (4.1) $ appears Hopf bifurcation when$ \tau_{1}=0.315 $ and$ \tau_{2}=0.25>0.2433 $ with$ \gamma_{1}=0.9 $ and$ \gamma_{2}=0.95 $ . -
Figure 11. Plot of the stability switching curves when
$ \gamma_{1}= \gamma_{2}=1 $ . -
Figure 12. The stable region of system
$ (4.1) $ with$ \gamma_{1}=\gamma_{2}=1 $ .