| Citation: |
İhsan Çelikkaya, Ahmet Güzel. FOUR NUMERICAL SCHEMES FOR SOLUTION OF BURGERS' EQUATION VIA OPERATOR SPLITTING TRIGONOMETRIC CUBIC B-SPLINE COLLOCATION METHOD[J]. Journal of Applied Analysis & Computation, 2023, 13(1): 313-328. doi: 10.11948/20220095
|
FOUR NUMERICAL SCHEMES FOR SOLUTION OF BURGERS' EQUATION VIA OPERATOR SPLITTING TRIGONOMETRIC CUBIC B-SPLINE COLLOCATION METHOD
-
Abstract
In this study, we have used operator splitting methods for numerical solutions of the Burgers' equation by given four different numerical schemes. To set these schemes, we divide the Burgers equation into two sub-problems according to the time term, as linear $ U_{t}=\mathcal{L}(U) $ and nonlinear $ U_{t}=\mathcal{N}(U) $. Then, numerical schemes have been obtained by the finite element method using trigonometric cubic B-spline basis for each sub-problem. Splitting $ \mathcal{L}\circ\mathcal{N} $, $ \mathcal{N}\circ\mathcal{L} $ Lie-Trotter and $ \mathcal{L}\circ\mathcal{N} \circ \mathcal{L} $, $ \mathcal{N\circ L\circ N} $ Strang splitting solution schemes have been used to obtain the solution of the main equation. Numerical results calculated with these schemes have been compared among themselves in terms of $ L_{2} $, $ L_{\infty} $ error norms and CPU time. Furthermore, the numerical results have been compared with some studies that solved the equation directly with the same method. It has been observed that the numerical results obtained with the proposed schemes are in agreement with the exact solution and other studies in the literature. All calculations are obtained using Matlab Version R2015a.
-
-
References
[1] B. Ay, İ. Dağ and M. Z. Görgülü, Trigonometric quadratic B-spline subdomain Galerkin algorithm for the Burgers' equation, Open Phys., 2015, 13, 400–406. DOI 10.1515/phys-2015-0059 doi: 10.1515/phys-2015-0059 [2] H. Bateman, Some recent researches on the motion of fluids, Monthly Weather Rev., 1915, 43, 163–170. doi: 10.1175/1520-0493(1915)43<163:SRROTM>2.0.CO;2 [3] J. M. Burgers, A mathematical model illustrating the theory of turbulence, Adv. Appl. Mech., 1948, 1, 171–199. [4] J. M. Burgers, Mathematical examples illustrating relations occurring in the theory of turbulent fluid motion, Trans. R. Neth. Acad. Sci. Amst., 1939, 17, 1–53. [5] A. G. Bratsos, A fourth-order numerical scheme for solving the modified Burgers' equation, Comput. Math. with Appl., 2010, 60, 1393–1400. doi: 10.1016/j.camwa.2010.06.021 [6] H. Brezis and F. Browder, Partial Differential Equations in the 20th Century, 1998, 135, 76–144. Article No. AI971713. [7] S. Blanes, F. Casas and A. Murua, Splitting and composition methods in the numerical integration of differential equations, Bol. Soc. Esp. Mat. Apl., 2008, 45, 89–145. [8] J. D. Cole, On a quasilinear parabolic equation occurring in aerodynamics, Quart. Appl. Math., 1951, 9, 225–236. doi: 10.1090/qam/42889 [9] İ. Dağ, Ö. E. Hepson and Ö. Kaçmaz, The trigonometric cubic B-spline Algorithm for Burgers' Equation, Int. J. Nonlinear Sci., 2017, 24(2), 120–128. [10] İ. Dağ, D. Irk and B. Saka, A numerical solution of the Burgers' equation using cubic B-splines, Appl. Math. Comput., 2005, 163, 199–211. doi: 10.1016/j.amc.2004.01.028 [11] İ. Dağ, D. Irk and A. Şahin, B-spline collocation methods for numerical solitions of the Burgers' equation, Math. Probl. Eng., 2005, 5, 521–538. DOI: 10.1155/MPE.2005.521 [12] Ö. Ersoy and G. Yiğit, Quartic Trigonometric Tension B-Spline Method for the Solution of the Advection-Diffusion Equation, Comput. Appl. Math., 2021, 40(141), 1–15. doi. org/10.1007/s40314-021-01526-2 doi: 10.1007/s40314-021-01526-2 [13] O. Ersoy, I. Dag and N. Adar, The exponential cubic B-spline algorithm for Burgers' equation, Ukr. Math. J., 2018, 70(6), 906–921. doi. org/10.1007/s11253-018-1541-9 doi: 10.1007/s11253-018-1541-9 [14] Ö. Ersoy, Generation Of The Trigonometric Cubic B-spline Collocation Solutions for the KuramotoSivashinsky(KS) Equation, AIP Conf. Proc., 2018, 470099. doi. org/10.1063/1.5044169 doi: 10.1063/1.5044169 [15] Ö. Ersoy, A Numerical Simulation of Kuramoto-Sivashinsky Equation in Reaction-Diffusion via Galerkin Method, Mathematical Science, 2021, 15, 199–206. doi. org/10.1007/s40096-021-00402-8 doi: 10.1007/s40096-021-00402-8 [16] Y. Gao, L. Le and B. Shi, Numerical solution of Burgers' equation by lattice Boltzmann method, Appl. Math. Comput., 2013, 219, 7685–7692. doi. org/10.1016/j.amc.2013.01.056 doi: 10.1016/j.amc.2013.01.056 [17] W. Hundsdorfer, Numerical Solution of Advection-Diffüsion-Reaction Equations, Lecture notes for PH. D. course, Thomas Stieltjes İnstitute, Amsterdam, 2000. [18] S. Kutluay, A. Esen and İ. Dağ, Numerical solutions of the Burgers' equation by the least-squares quadratic B-spline finite element method, J. Comput. Appl. Math., 2004, 167, 21–33. doi: 10.1016/j.cam.2003.09.043 [19] S. Kutluay and A. Esen, A Lumped galerkin method for solving the Burgers' equation, Int. J. Comput. Math., 2004, 81, 1433–1444. DOI: 10.1080/00207160412331286833 [20] P. E. Koch, Multivariate trigonometric B-splines, J. Approx. Theory, 1988, 54, 162–168. doi: 10.1016/0021-9045(88)90016-0 [21] R. C. Mittal and R. K. Jain, Numerical solutions of nonlinear Burgers' equation with modified cubic B-splines collocation method, Appl. Math. Comput., 2012, 218, 7839–7855. doi: 10.1016/j.amc.2012.01.059 [22] G. I. Marchuk, Some application of splitting-up methods to the solution of mathematical physics problems, Aplikace matematiky, 1968, 13, 103–132. [23] A. T. Onarcan and Ö. Ersoy, Higher order Trigonometric B-spline Algorithms to the solution of Coupled Burgers' Equation, AIP Conf. Proc., 2018, 1926, 020044. doi. org/10.1063/1.5020493 doi: 10.1063/1.5020493 [24] B. Saka and İ. Dağ, Quartic B-spline collocation method to the numerical solutions of the Burgers' equation, Chaos Solitons Fractals, 2007, 32, 1125–1137. doi: 10.1016/j.chaos.2005.11.037 [25] B. Saka and İ. Dağ, A numerical study of the Burgers' equation, J. Franklin Inst., 2008, 345, 328–348. doi: 10.1016/j.jfranklin.2007.10.004 [26] M. Seydaoğlu, U. Erdoğan and T. Öziş, Numerical solution of Burgers' equation with high order splitting methods, J. Comput. Appl. Math., 2016, 291, 410–421. doi: 10.1016/j.cam.2015.04.021 [27] G. Strang, On the construction and comparison of difference schemes, SIAM J. Numer. Anal., 1968, 5, 506–517. doi: 10.1137/0705041 [28] H. F. Trotter, On the product of semi-groups of operators, Proc. American Math. Society, 1959, 10, 545–551. doi: 10.1090/S0002-9939-1959-0108732-6 [29] Y. Uçar, N. M. Yağmurlu and İ. Çelikkaya, Numerical Solution of Burger's Type Equation Using Finite Element Collocation Method with Strang Splitting, M. S. A. E. N., 2020, 8(1), 29–45. DOI. ORG/10.36753/MATHENOT. 598635 [30] G. Walz, Identities for trigonometric B-splines with an application to curve design, BIT, 1997, 37, 189–201. doi: 10.1007/BF02510180 -
-
Figures(3) / Tables(9)
Export File
Citation
İhsan Çelikkaya, Ahmet Güzel. FOUR NUMERICAL SCHEMES FOR SOLUTION OF BURGERS' EQUATION VIA OPERATOR SPLITTING TRIGONOMETRIC CUBIC B-SPLINE COLLOCATION METHOD[J]. Journal of Applied Analysis & Computation, 2023, 13(1): 313-328. doi: 10.11948/20220095
Format
Content
DownLoad:
-
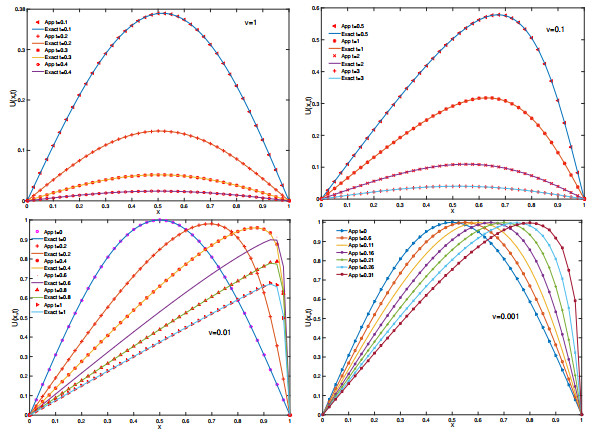
Figure 1.
Exact and numerical solutions of Problem 1 obtained by
$ \mathcal{ N\circ L} $ $ \nu $ $ t $ $ h=0.025, $ $ \Delta t=0.0001 $ -
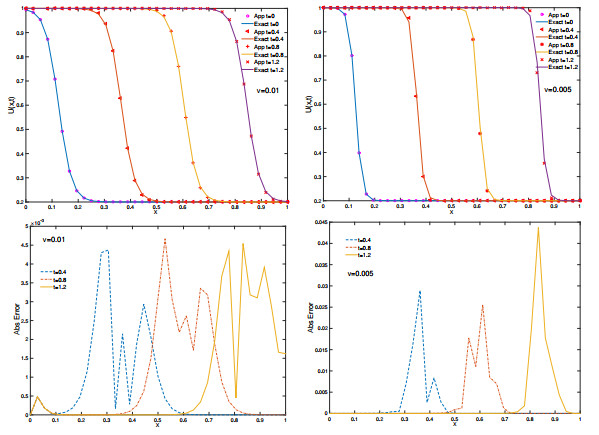
Figure 2.
Physical behaviors of the solution and absolute error of problem 2 obtained by
$ \mathcal{N\circ L} $ $ \nu $ $ t $ $ h=1/36, $ $ \Delta t=0.01 $ -
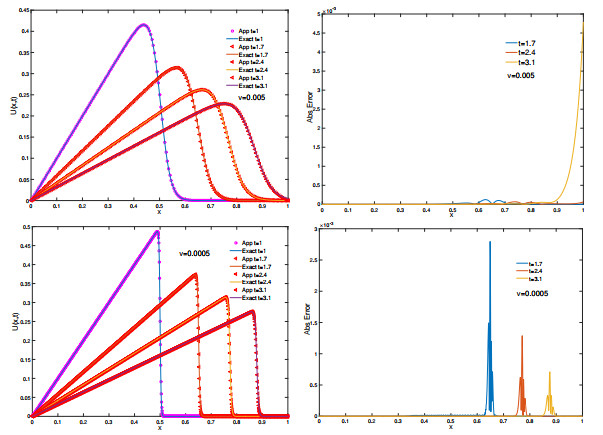
Figure 3.
Physical behaviors of the solution and absolute error of problem 3 obtained by
$ \mathcal{N\circ L\circ N} $ $ \nu=0.005 $ $ h=0.005 $ $ \nu=0.0005 $ $ h=0.001 $ $ \Delta t=0.01 $