| Citation: |
Xing Lü, Xuejiao He. BÄCKLUND TRANSFORMATION TO SOLVE THE GENERALIZED (3+1)-DIMENSIONAL KP-YTSF EQUATION AND KINKY PERIODIC-WAVE, WRONSKIAN AND GRAMMIAN SOLUTIONS[J]. Journal of Applied Analysis & Computation, 2023, 13(2): 758-781. doi: 10.11948/20220110
|
BÄCKLUND TRANSFORMATION TO SOLVE THE GENERALIZED (3+1)-DIMENSIONAL KP-YTSF EQUATION AND KINKY PERIODIC-WAVE, WRONSKIAN AND GRAMMIAN SOLUTIONS
-
Abstract
The Kadomtsev-Petviashvili equation is considered to be a basic model describing nonlinear dispersive wave in fluids, which is an integrable equation with two spatial dimensions. The Yu-Toda-Sasa- Fukuyama equation plays a crucial role in fluid dynamics, plasma physics and weakly dispersive media. In this paper, we investigate a generalized (3+1)-dimensional Kadomtsev-Petviashvili-Yu-Toda-Sasa-Fukuyama equation, and multiple types of solutions are derived. With symbolic computation, a class of kinky periodic-wave solutions, determinant solutions and the bilinear Bäcklund transformation are constructed. We obtain two types of determinant solutions, that is, Wronskian and Grammian solutions. By choosing the appropriate matrix elements of determinants, many kinds of solutions are derived. In addition to the soliton solutions, the complexiton solutions and rational solutions are given. As illustrative examples, a few particular solutions are computed and plotted.
-
-
References
[1] S. Chen, X. Lü, M. Li and F. Wang, Derivation and simulation of the M-lump solutions to two (2+1)-dimensional nonlinear equations, Physica Scripta, 2021, 96, 095201. DOI: 10.1088/1402-4896/abf307 [2] S. Chen, X. Lü and X. Tang, Novel evolutionary behaviors of the mixed solutions to a generalized Burgers equation with variable coefficients, Communications in Nonlinear Science and Numerical Simulation, 2020, 95, 105628. DOI: 10.1016/j.cnsns.2020.105628. [3] Y. Yin, X. Lü and W. Ma, Bäcklund transformation, exact solutions and diverse interaction phenomena to a (3+1)-dimensional nonlinear evolution equation, Nonlinear Dynamics, 2022, 108, 4181. doi: 10.1007/s11071-021-06531-y [4] J. H. Choi and H. Kim, Soliton solutions for the space-time nonlinear partial differential equations with fractional-orders, Chinese Journal of Physics, 2017, 55(2), 556-565. doi: 10.1016/j.cjph.2016.10.019 [5] T. Congy, G. A. El and M. A. Hoefer, Interaction of linear modulated waves and unsteady dispersive hydrodynamic states with application to shallow water waves, Journal of Fluid Mechanics, 2019, 875, 1145-1174. doi: 10.1017/jfm.2019.534 [6] S. Chen and X. Lü, Lump and lump-multi-kink solutions in the (3+1)-dimensions, Communications in Nonlinear Science and Numerical Simulation, 2022, 109, 106103. doi: 10.1016/j.cnsns.2021.106103 [7] M. T. Darvishi and M. Najafi, A modification of extended homoclinic test approach to solve the (3+1)-dimensional potential-YTSF equation, Chinese Physics Letters, 2011. DOI: 10.1088/0256-307X/28/4/040202. [8] M. Dong, S. Tian, X. Wang and T. Zhang, Lump-type solutions and interaction solutions in the (3+1)-dimensional potential Yu-Toda-Sasa-Fukuyama equation, Analysis and Mathematical Physics, 2019, 9, 1511-1523. doi: 10.1007/s13324-018-0258-0 [9] T. Fang and Y. Wang, Lump-stripe interaction solutions to the potential Yu-Toda-Sasa-Fukuyama equation, Analysis and Mathematical Physics, 2019, 9, 1481-1495. doi: 10.1007/s13324-018-0255-3 [10] H. A. Ghany, S. K. Elagan and A. Hyder, Exact travelling wave solutions for stochastic fractional Hirota-Satsuma coupled KdV equations, Chinese Journal of Physics, 2015, 53, 153-166. [11] B. Liu, X. Zhang, B. Wang and X. Lü, Rogue waves based on the coupled nonlinear Schrodinger option pricing model with external potential, Modern Physics Letters B, 2022, 36, 2250057. [12] R. Hirota, The Direct Method in Soliton Theory, Cambridge University Press, England, 2004. [13] A. V. Holden, Nonlinear science-The impact of biology, International Journal of Bifurcation and Chaos, 1997. DOI:10.1016/S0016-0032(97)00029-X. [14] L. Huang and J. Zhang, Grammian solution and Wronskian solution for the variable-coefficient Kdv equation, Journal of Xiamen University (Natural Science), 2015, 54, 354-357. [15] Y. Hu, H. Chen and Z. Dai, New kink multi-soliton solutions for the (3+1)-dimensional potential Yu-Toda-Sasa-Fukuyama equation, Appl. Math. Comput., 2014, 234, 548-556. [16] X. Lü and W. Ma, Study of lump dynamics based on a dimensionally reduced Hirota bilinear equation, Nonlinear Dynamics, 2016, 85, 1217. doi: 10.1007/s11071-016-2755-8 [17] M. Karpov, M. H. P. Pfeiffer and J. Liu, Photonic chip-based soliton frequency combs covering the biological imaging window, Nature Communications, 2017. DOI: 10.1038/S41467-018-03471-X. [18] R. Lin, Y. Zeng and W. Ma, Solving the KdV hierarchy with self-consistent sources by inverse scattering method, Physica A, 2001, 291, 287-298. doi: 10.1016/S0378-4371(00)00519-7 [19] X. Lü and S. Chen, New general interaction solutions to the KPI equation via an optional decoupling condition approach, Communications in Nonlinear Science and Numerical Simulation, 2021, 103, 105939-105949. doi: 10.1016/j.cnsns.2021.105939 [20] X. Lü, Y. Hua, S. Chen and X. Tang, Integrability characteristics of a novel (2+1)-dimensional nonlinear model: Painleve analysis, soliton solutions, Backlund transformation, Lax pair and infinitely many conservation laws, Communications in Nonlinear Science and Numerical Simulation, 2020. DOI: 10.1016/j.cnsns.2020.105612. [21] X. Lü, S. Chen and W. Ma, Constructing lump solutions to a generalized Kadomtsev-Petviashvili-Boussinesq equation, Nonlinear Dynamics, 2016, 86, 523-534. doi: 10.1007/s11071-016-2905-z [22] X. Lü and S. Chen, Interaction solutions to nonlinear partial differential equations via Hirota bilinear forms: One-lump-multi-stripe and one-lump-multi-soliton types, Nonlinear Dynamics, 2021, 103, 947-977. doi: 10.1007/s11071-020-06068-6 [23] V. B. Matveev and M A. Salle, Darboux Transformations and Solitons, Springer, Berlin, 1991. [24] Y. Matsuno, Bilinear Bäcklund transformation for the KdV equation with a source, Journal of Physics A: Mathematical and General, 1999, 24(6), L273-L277. [25] W. Ma, Riemann-Hilbert problems and soliton solutions of nonlocal reverse-time NLS hierarchies, Acta Mathematica Scientia, 2022, 42, 127-140. doi: 10.1007/s10473-022-0106-z [26] W. Ma, Riemann-Hilbert problems and inverse scattering of nonlocal real reverse-spacetime matrix AKNS hierarchies, Physica D-Nonlinear Phenomena, 2021. DOI: 10.1016/j.physd.2021.133078. [27] W. Ma, Nonlocal PT-symmetric integrable equations and related Riemann-Hilbert problems, Partial Differential Equations in Applied Mathematics, 2021. DOI: 10.1016/j.padiff.2021.100190. [28] W. Ma, Riemann-Hilbert problems and soliton solutions of type (λ*, -λ*) reduced nonlocal integrable mKdV hierarchies, Mathematics, 2022. DOI: 10.3390/math10060870. [29] X. Lü, H. Hui, F. Liu and Y. Bai, Stability and optimal control strategies for a novel epidemic model of COVID-19, Nonlinear Dynamics, 2021, 106, 1491. doi: 10.1007/s11071-021-06524-x [30] M. Yin, Q. Zhu and X. Lü, Parameter estimation of the incubation period of COVID-19 based on the doubly interval-censored data model, Nonlinear Dynamics, 2021, 106, 1347. doi: 10.1007/s11071-021-06587-w [31] W. Ma, Type (λ*, -λ*) reduced nonlocal integrable mKdV equations and their soliton solutions, Applied Mathematics Letters, 2022. DOI: 10.1016/j.aml.2022.108074. [32] W. Ma, Nonlocal integrable mKdV equations by two nonlocal reductions and their soliton solutions, Journal of Geometry and Physics, 2022. DOI: 10.1016/j.geomphys.2022.104522. [33] W. Ma, Lump solutions to the Kadomtsev-Petviashvili equation, Physics Letters A, 2015, 379, 1975-1978. doi: 10.1016/j.physleta.2015.06.061 [34] A. Peleg, Q. M. Nguyen and T. T. Huynh, Stable scalable control of soliton propagation in broadband nonlinear optical waveguides, European Physical Journal D, 2017. DOI: 10.48550/arXiv.1506.01124. [35] D. E. Pelinovsky and Y. Shimabukuro, Existence of Global Solutions to the Derivative NLS Equation with the Inverse Scattering Transform Method, International Mathematics Research Notices, 2016. DOI: 10.1093/imrn/rnx051. [36] C. Rogers and W. R. Shadwick, Bäcklund transformation and their application, Academic Press, American, 1982. [37] S. H. Sabzpoushan, A flexible nonlinear model for simulating growth systems, Communications in Nonlinear ence and Numerical Simulation, 2019, 82(1), 105009-105026. [38] J. Satsuma, A Wronskian representation of N-soliton solutions of nonlinear evolution equations, Journal of the Physical Society of Japan, 2007, 46(1), 359-360. [39] M. Singh, New exact solutions for (3+1)-dimensional Jimbo-Miwa equation, Nonlinear Dynamics, 2016, 84, 875-880. doi: 10.1007/s11071-015-2533-z [40] L. Song and H. Zhang, A new variable coefficient Korteweg-de Vries equation-based sub-equation method and its application to the (3+1)-dimensional potential-YTSF equation, Applied Mathematics and Computation, 2007, 189, 560-566. doi: 10.1016/j.amc.2006.11.119 [41] V. A. Vladimirov, E. V. Kutafina and B. Zorychta, On the non-local hydrodynamic-type system and its soliton-like solutions, Journal of Physics A Mathematical and Theoretical, 2012, 45(8), 1262-1275. [42] J. Xia, Y. Zhao and X. Lü, Predictability, fast calculation and simulation for the interaction solution to the cylindrical Kadomtsev-Petviashvili equation, Communications in Nonlinear Science and Numerical Simulation, 2020, 88, 105260. DOI: 10.1016/j.cnsns.2020.105260. [43] H. Xu, W. Ruan, Y. Zhang and X. Lü, Multi-exponential wave solutions to two extended Jimbo-Miwa equations and the resonance behavior, Applied Mathematics Letters, 2020, 99, 105976-105986. doi: 10.1016/j.aml.2019.07.007 [44] Y. Yin, S. Chen and X. Lü, Localized characteristics of lump and interaction solutions to two extended Jimbo-Miwa equations, Chin. Phys. B, 2020, 29, 120502. DOI: 10.1088/1674-1056/aba9c4. [45] D. Wang, B. Guo and X. Wang, Long-time asymptotics of the focusing Kundu-Eckhaus equation with nonzero boundary conditions, Journal of Differential Equations, 2019, 266, 5209. doi: 10.1016/j.jde.2018.10.053 [46] Y. Zhao, J. Xia and X. Lü, The variable separation solution, fractal and chaos in an extended coupled (2+1)-dimensional Burgers system, Nonlinear Dynamics, 2022, 108, 4195. doi: 10.1007/s11071-021-07100-z [47] L. Zhang and X. Liu, New exact solutions and conservation laws to (3+1)-dimensional potential-YTSF equation, Communications in Theoretical Physics, 2006, 45, 487-492. doi: 10.1088/0253-6102/45/3/022 -
-
Figures(7)
Export File
Citation
Xing Lü, Xuejiao He. BÄCKLUND TRANSFORMATION TO SOLVE THE GENERALIZED (3+1)-DIMENSIONAL KP-YTSF EQUATION AND KINKY PERIODIC-WAVE, WRONSKIAN AND GRAMMIAN SOLUTIONS[J]. Journal of Applied Analysis & Computation, 2023, 13(2): 758-781. doi: 10.11948/20220110
Format
Content
DownLoad:
-
Figure 1.
The kinky periodic-wave solution via Eq. (2.4) with
$ c_{1}=-\frac{1}{4}, c_{2}=0, c_{3}=-\frac{3}{4} $ $ a_{2}=b_{1}=b_{2}=d_{2}=1 $ $ \delta_{1}=2 $ $ t=1 $ $ z=1 $ -
Figure 2.
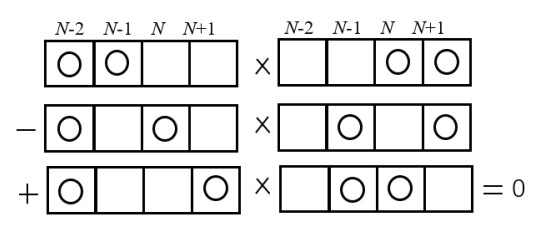
Maya chart of Eq. (3.5): the Plücker relation.
-
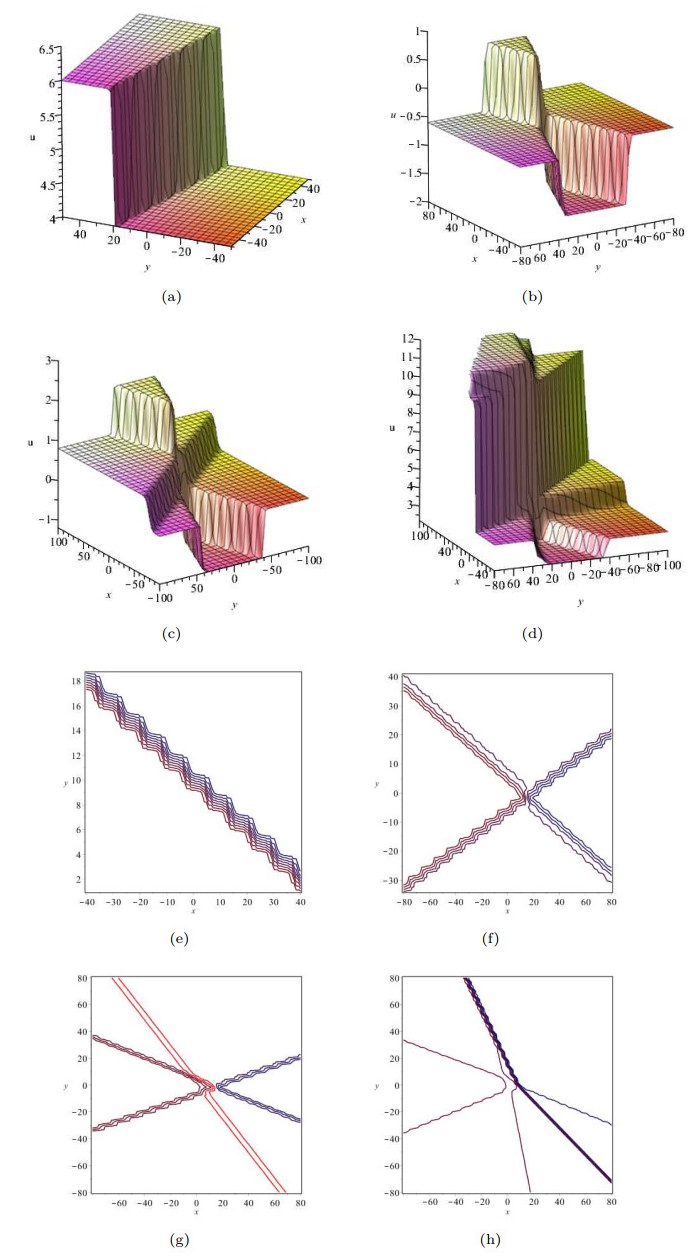
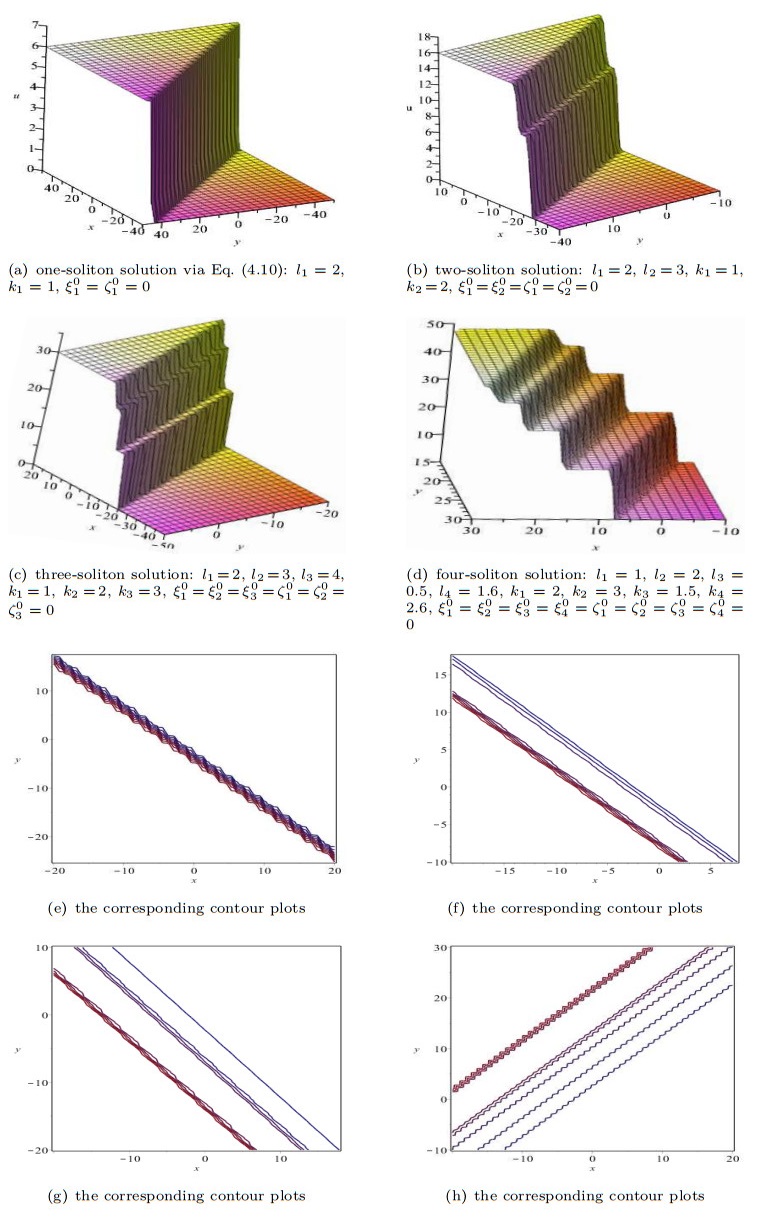
Figure 3.
Soliton solutions to Eq. (1.7) with
$ c_{1}=-1, c_{2}=1, c_{3}=2 $ $ z=1 $ $ t=1 $ $ \gamma=1 $ $ l_{1}=2 $ $ k_{1}=3 $ $ \xi_{1}^{0}=\zeta_{1}^{0}=0 $ $ l_{1}=1 $ $ l_{2}=-1.2 $ $ k_{1}=1.5 $ $ k_{2}=-1.8 $ $ \xi_{1}^{0}=\xi_{2}^{0}=\zeta_{1}^{0}=\zeta_{2}^{0}=0 $ $ l_{1}=1 $ $ l_{2}=-1.2 $ $ l_{3}=0.2 $ $ k_{1}=1.6 $ $ k_{2}=-1.8 $ $ k_{3}=0.6 $ $ \xi_{1}^{0}=\xi_{2}^{0}=\xi_{3}^{0}=\zeta_{1}^{0}=\zeta_{2}^{0}=\zeta_{3}^{0}=0 $ $ l_{1}=1 $ $ l_{2}=0.4 $ $ l_{3}=1.8 $ $ l_{4}=-1 $ $ k_{1}=1.5 $ $ k_{2}=-0.2 $ $ k_{3}=2 $ $ k_{4}=-1.5 $ $ \xi_{1}^{0}=\xi_{2}^{0}=\xi_{3}^{0}=\xi_{4}^{0}=\zeta_{1}^{0}=\zeta_{2}^{0}=\zeta_{3}^{0}=\zeta_{4}^{0}=0 $ -
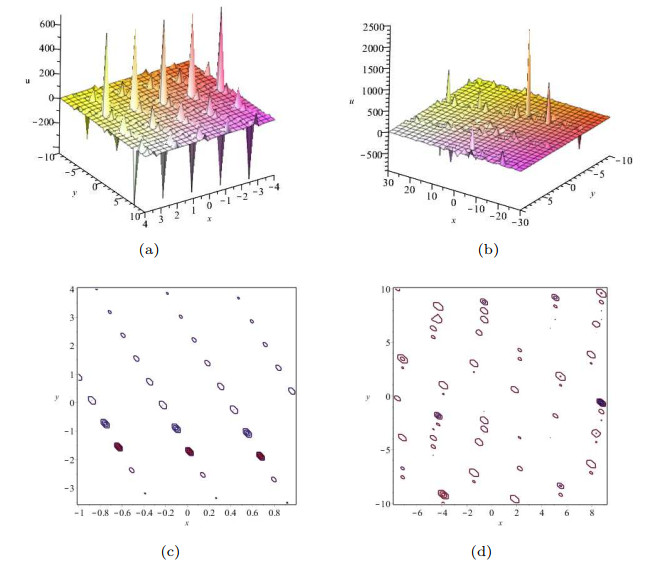
Figure 4.
The complexiton solution to Eq. (1.7) with
$ c_{1}=1, c_{2}=2, c_{3}=3 $ $ t=1 $ $ z=1 $ $ \gamma=1 $ $ N=1 $ $ \alpha_{11}=2 $ $ \beta_{11}=1 $ $ N=2 $ $ \alpha_{11}=2, \alpha_{12}=1 $ $ \beta_{11}=1, \beta_{12}=2 $ -
Figure 5.
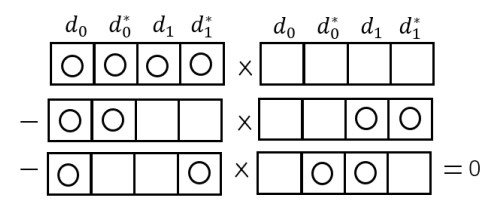
Maya chart of Eq. (4.7): the Jacobi identity.
-
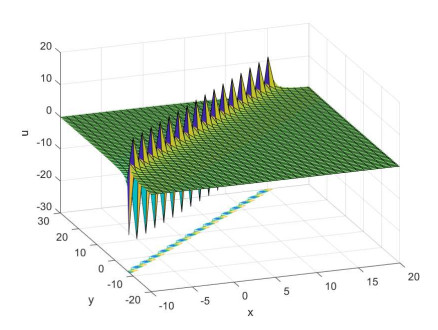
Figure 6.
Soliton solutions to Eq. (1.7) with
$ z=1 $ $ t=1 $ $ \gamma=1 $ -
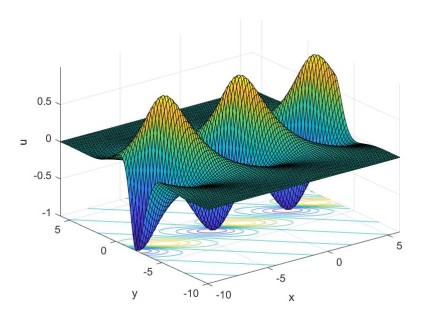
Figure 7.
Plot of the rational solution and the contour via Eq. (5.11) with
$ c_{1}=1, c_{2}=-2 $ $ z=1 $ $ t=3 $