| Citation: |
Hongjin He, Dongmei Xiao. ON THE GLOBAL CENTER OF PLANAR POLYNOMIAL DIFFERENTIAL SYSTEMS AND THE RELATED PROBLEMS[J]. Journal of Applied Analysis & Computation, 2022, 12(3): 1141-1157. doi: 10.11948/20220157
|
ON THE GLOBAL CENTER OF PLANAR POLYNOMIAL DIFFERENTIAL SYSTEMS AND THE RELATED PROBLEMS
-
Abstract
In the paper we characterize planar polynomial differential systems with a global center, that is, every orbit of the system is a periodic orbit in $ \mathbb{R}^2 $. Further, we give algebraic sufficient and necessary conditions for potential systems and Liénard systems which have a global center, respectively. Last we discuss some related problems.
-
-
References
[1] A. Cima, A. Gasull and F. Manosas, On Polynomial Hamiltonian Planar Vector Fields, Journal of Differential Equations, 1993, 106, 367–383. doi: 10.1006/jdeq.1993.1112 [2] J. P. Francoise, H. He and D. Xiao. The number of limit cycles bifurcating from the period annulus of quasi-homogeneous Hamiltonian systems at any order, Journal of Differential Equations, 2021, 276, 1–24. doi: 10.1016/j.jde.2020.12.014 [3] J. P. Francoise and D. Xiao. Perturbation theory of a symmetric center within Liénard equations, Journal of Differential Equations, 2015, 259, 2408–2429. doi: 10.1016/j.jde.2015.03.039 [4] M. Galeoti and M. Villarini, Monodromic Unbounded Polycycles, Ann. Mat. Pura Appl. IV CLXXI, 1996, 83–105. [5] A. Gasull and J. Torregrosa, Center Problem for Several Differential Equations via Cherkas' Method, Journal of Mathematical Analysis and Applications, 1998, 228, 322–343. doi: 10.1006/jmaa.1998.6112 [6] M. Han, Bifurcation Theory of Limit Cycles, Science Press, Beijing, 2013. [7] H. He, J. Llibre and D. Xiao, Planar polynomial Hamiltonian differential systems with global centers, Sci. Sin. Math. (in chinese), 2021, 51, 1–12. doi: 10.1360/SSM-2019-0345 [8] H. He and D. Xiao, The bound on number of limit cycles bifurcating from any bounded period annulus of quasi-homogeneous polynomial systems at any order, preprint, 2022. [9] C. Li and W. Li, Weak Hilbert's 16th problem and the related research, Adv. Math. (in chinese), 2010, 39, 513–526. [10] J. Li, Hilbert's 16th problem and bifurcations of planar polynomial vector fields, Internat. J. Bifur. Chaos Appl. Sci. Engrg., 2003, 13, 47–106. doi: 10.1142/S0218127403006352 [11] W. Li, J. Llibre, J. Yang and Z. Zhang, Limit cycles bifurcating from the period annulus of quasi-homogeneous centers, Journal of Dynamics and Differential Equations, 2009, 21, 133–152 doi: 10.1007/s10884-008-9126-1 [12] J. Llibre, Centers: their integrability and relations with the divergence, Applied Mathematics and Nonlinear Sciences, 2016, 1, 79–86. doi: 10.21042/AMNS.2016.1.00007 [13] D. Schlomiuk, Algebraic particular integrals, integrability and the problem of the center, Trans. Amer. Math. Soc., 1993, 338, 799–841. doi: 10.1090/S0002-9947-1993-1106193-6 [14] L. Yang, Recent advances on determining the number of real roots of parametric polynomials, J. Symbolic Computation, 1999, 28, 225–242. doi: 10.1006/jsco.1998.0274 [15] X. Zhang, Integrability of dynamical systems: algebra and analysis, Developments in Mathematics, Springer, Singapore, 2017, 47. -
-
Figures(3)
Export File
Citation
Hongjin He, Dongmei Xiao. ON THE GLOBAL CENTER OF PLANAR POLYNOMIAL DIFFERENTIAL SYSTEMS AND THE RELATED PROBLEMS[J]. Journal of Applied Analysis & Computation, 2022, 12(3): 1141-1157. doi: 10.11948/20220157
Format
Content
DownLoad:
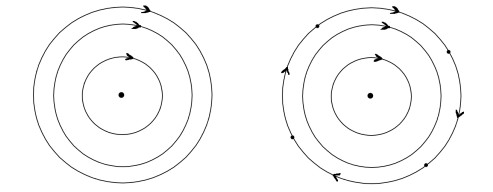
- Figure 1. Two kinds of global phase portraits for planar polynomial systems with a global center.
-
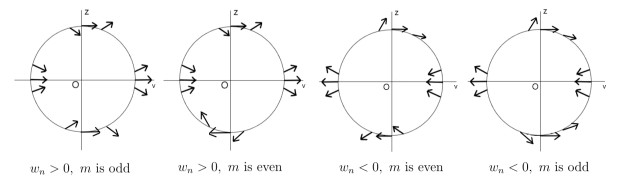
Figure 2. The changes on the direction of vector field (3.2) near the intersection points of
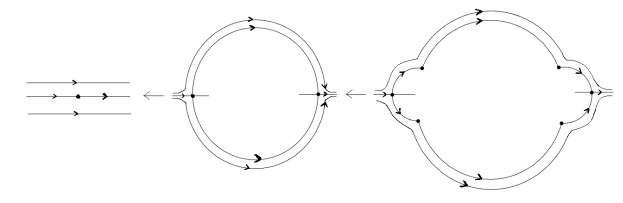
$ S_{\varepsilon} $ and$ vz=0 $ . - Figure 3. The process of blowing up for the equilibrium point of system (3.12).