| Citation: |
Haichao Xiong, Jun Zhang, Weinian Zhang. USE SLOW-SPREAD OF ONCOLYTIC VIRUS TO DEPRESS EXPONENTIAL GROWTH OF TUMOR CELLS[J]. Journal of Applied Analysis & Computation, 2022, 12(3): 1158-1185. doi: 10.11948/20220168
|
USE SLOW-SPREAD OF ONCOLYTIC VIRUS TO DEPRESS EXPONENTIAL GROWTH OF TUMOR CELLS
-
Abstract
In this paper we analyze an ODE model for oncolytic dynamics of exponential growth of tumor cells with slow-spread of virus, which was modeled by Komarova and Wodarz but not discussed yet. The involved four parameters render finding equilibria to be a difficult problem of algebraic varieties. We discuss resultants of polynomials to give complete conditions for distribution and qualitative properties of equilibria. We prove that the degenerate equilibrium is either a saddle-node or a cusp, which is of codimension infinity. Moreover, we prove that the equilibrium of center type is either a rough center or a weak center of order 1. Furthermore, analyzing equilibria at infinity, showing existence of a homoclinic orbit and giving nonexistence of limit cycles, we exhibit global phase portraits, which suggest strategies of tumor control.
-
Keywords:
- Tumor control /
- cusp /
- weak center /
- homoclinic orbit /
- resultant
-
-
References
[1] Ž. Bajzer, T. Carr, K. Josić, S. J. Russell and D. Dingli, Modeling of cancer virotherapy with recombinant measles viruses, J. Theor. Biol., 2008, 252, 109–122. doi: 10.1016/j.jtbi.2008.01.016 [2] R. I. Bogdanov, Versal deformation of a singularity of a vector field on the plane in the case of zero eigenvalues, Selecta Math. Sov., 1981, 1, 389–421. [3] J. Carr, S. N. Chow and J. K. Hale, Abelian integrals and bifurcation theory, J. Differential Eq., 1985, 59, 413–436. doi: 10.1016/0022-0396(85)90148-2 [4] C. Chicone and M. Jacobs, Bifurcation of critical periods for plane vector fields, Trans. Amer. Math. Soc., 1989, 157(2), 433–486. [5] S. N. Chow, C. Li and D. Wang, Normal Forms and Bifurcation of Planar Vector Fields, Cambridge Univ. Press, Cambridge, 1994. [6] S. N. Chow and J. A. Sanders, On the number of critical periods of the period, J. Differential Eq., 1986, 64, 51–66. doi: 10.1016/0022-0396(86)90071-9 [7] D. Dingli, M. D. Cascino, K. Josić, S. J. Russel and Ž. Bajzer, Mathematical modeling of cancer radiovirotherapy, Math. Biosci., 2006, 199(1), 55–78. doi: 10.1016/j.mbs.2005.11.001 [8] F. Dumortier, R. Roussarie and J. Sotomayor, Generic 3-parameter families of vector fields on the plane, unfolding a singularity with nilpotent linear part. The cusp case of codimension 3, Ergod. Theor. Dyn. Syst., 1987, 7, 375–413. doi: 10.1017/S0143385700004119 [9] I. A. García, Transcendental limit cycles via the structure of arbitrary degree invariant algebaic curves of polynomial planar vector fields, Rocky Mountain J. Math., 2005, 35(2), 505–515. [10] I. M. Gelfand, M. M. Kapranov and A. V. Zelevinsky, Discriminants, Resultants, and Multidimensional Determinants, Birkhäuser, Boston, 1994. [11] J. Guckenheimer and P. Holmes, Nonlinear Oscillations, Dynamical Systems and Bifurcations of Vector Fields, Springer, New York, 1995. [12] P. B. Hajeri, N. S. Sharma and M. Yamamoto, Oncolytic adenoviruses: strategies for improved targeting and specificity, Cancers, 2020, 12(6), 1504. doi: 10.3390/cancers12061504 [13] M. Han and P. Yu, Normal Forms, Melnikov Functions and Bifurcations of Limit Cycles, Springer, New York, 2012. [14] H. Huang, Y. Liu, W. Liao, et al., Oncolytic adenovirus programmed by synthetic gene circuit for cancer immunotherapy, Nat. commun., 2019, 10(1), 1–15. doi: 10.1038/s41467-018-07882-8 [15] A. Jeffrey, Complex Analysis and Applications, 2nd edition, Chapman & Hall/CRC, New York, 2005. [16] P. Joyal, The cusp of order $n$, J. Differential Eq., 1990, 88(1), 1–14. doi: 10.1016/0022-0396(90)90105-X [17] N. L. Komarova and D. Wodarz, ODE models for oncolytic virus dynamics, J. Theor. Biol., 2010, 263(4), 530–543. doi: 10.1016/j.jtbi.2010.01.009 [18] C. Li and Z. Zhang, A criterion for determining the monotonicity of the ratio of two Abelian integrals, J. Differential Eq., 1996, 124(2), 407–424. doi: 10.1006/jdeq.1996.0017 [19] M. Marden, Geometry of Polynomials, 2nd edition, American Mathematical Society, Providence, RI, 1966. [20] V. K. Mel'nikov, On the stability of a center for time-periodic perturbations, Trudy Moskovskogo Matematicheskogo Obshchestva, 1963, 12, 3–52. [21] A. S. Novozhilov, F. S. Berezovskaya, E. V. Koonin and G. P. Karev, Mathematical modeling of tumor therapy with oncolytic viruses: Regimes with complete tumor elimination, within the framework of deterministic models, Biol. Direct, 2006, 1(1), 1–18. doi: 10.1186/1745-6150-1-1 [22] R. Oliveira, D. Schlomiuk, A. M. Travaglini and C. Valls, Geometry, integrability and bifurcation diagrams of a family of quadratic differential systems as application of the Darboux theory of integrability, Electron. J. Qual. Theor. Differential Eq., 2021, 2021(45), 1–90. [23] L. Perko, Diffenrential Equations and Dynamical Systems, Spinger, New York, 1991. [24] M. J. Prelle and M. F. Singer, Elementary first integrals of differential equations, Trans. Amer. Math. Soc., 1983, 279, 215–229. doi: 10.1090/S0002-9947-1983-0704611-X [25] V. Romanovski and D. Shafer, The Center and Cyclicity Problems: a Computational Algebra Approach, Birkhäuser, Boston, 2009. [26] W. Si and W. Zhang, Control exponential growth of tumor cells with slow spread of oncolytic virus, J. Theor. Biol., 2015, 367, 111–129. doi: 10.1016/j.jtbi.2014.11.015 [27] K. M. Storey and T. L. Jackson, An agent-based model of combination oncolytic viral therapy and anti-PD-1 immunotherapy reveals the importance of spatial location when treating glioblastoma, Cancers, 2021, 13(21), 5314. doi: 10.3390/cancers13215314 [28] F. Takens, Forced oscillations and bifurcations, Global Analysis of Dynamical Systems, ed. H. W. Broer et al., Institute of Physics Publishing, Bristol, Philadelphia, 2001, 1–61. [29] L. M. Wein, J. Wu and D. H. Kirn, Validation and analysis of a mathematical model of a replication-competent oncolytic virus for cancer treatment: implications for virus design and delivery, Cancer Res., 2003, 63(6), 1317–1324. [30] D. Wodarz, Viruses as antitumor weapons: defining conditions for tumor remission, Cancer Res., 2001, 61(8), 3501–3507 [31] J. Zhang, Dynamics of an oncolytic virus model, Nonlinear Anal. : Real World Appl., 2021, 57, 103203. doi: 10.1016/j.nonrwa.2020.103203 [32] Z. Zhang, T. Ding, W. Huang and Z. Dong, Qualitative Theory of Differential Equations, American Mathematical Society, Providence, RI, 1992. -
-
Figures(5) / Tables(2)
Export File
Citation
Haichao Xiong, Jun Zhang, Weinian Zhang. USE SLOW-SPREAD OF ONCOLYTIC VIRUS TO DEPRESS EXPONENTIAL GROWTH OF TUMOR CELLS[J]. Journal of Applied Analysis & Computation, 2022, 12(3): 1158-1185. doi: 10.11948/20220168
Format
Content
DownLoad:
-
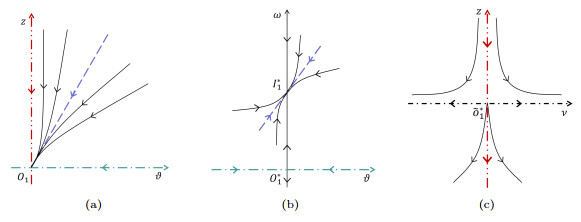
Figure 1. (a) Phase portrait of system (5.1) near
$ O_1 $ . (b) Phase portrait of system (5.2) near the$ \omega $ -axis. (c) Phase portrait of system (5.3) near$ \widetilde{O}^*_1 $ . -
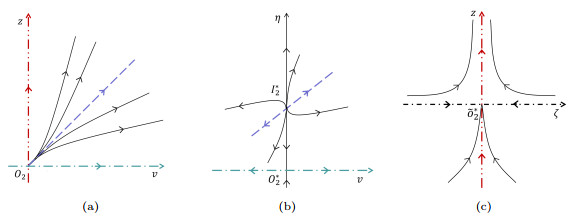
Figure 2. (a) Phase portrait of system (5.4) near
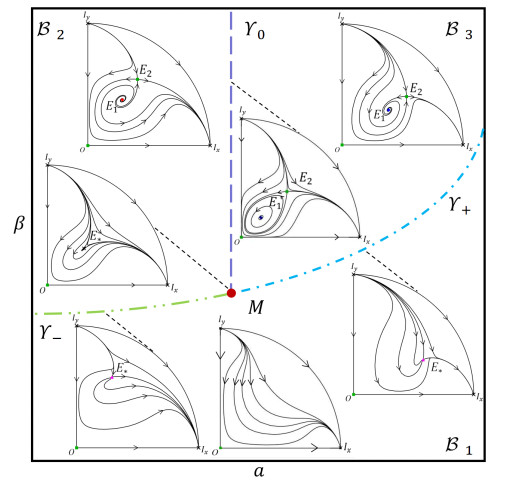
$ O_2 $ . (b) Phase portrait of system (5.5) near the$ \eta $ -axis. (c) Phase portrait of system (5.6) near$ \widetilde{O}^*_2 $ . - Figure 3. Global phase portraits of system (1.2).
-
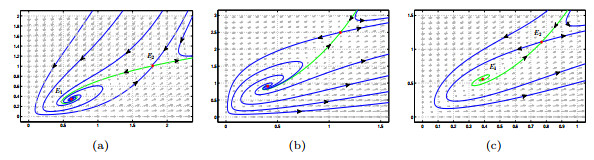
Figure 4. Simulations of system (1.2). (a) No cycles for
$ (\beta,a,\varepsilon_1,\varepsilon_2)=(26/5,16/9,1/2,1/4) $ . (b) No cycles for$ (\beta,a,\varepsilon_1,\varepsilon_2)=(315/100,4/9,1/2,1) $ . (c) No cycles for$ (\beta,a,\varepsilon_1,\varepsilon_2)=(14/5,25/36,1/2,1/16) $ . -
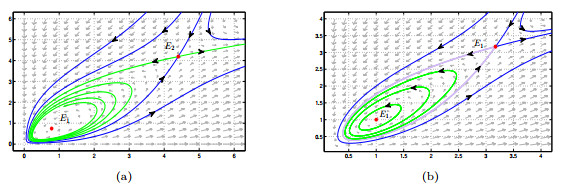
Figure 5. Simulations of system (1.2). (a) One saddle and one stable focus when
$ (\beta,a,\varepsilon_1,\varepsilon_2)=(13/2,21/20,1,1) $ . (b) Coexistence of homoclinic orbit and center when$ (\beta,a,\varepsilon_1,\varepsilon_2)=(6,1,1,1) $ .