| Citation: |
Zongguang Li, Zhengrong Liu. ELLIPTIC SINGULAR WAVE SOLUTIONS AND THEIR LIMITS OF A SIMPLE EQUATION[J]. Journal of Applied Analysis & Computation, 2022, 12(3): 1195-1210. doi: 10.11948/20220193
|
ELLIPTIC SINGULAR WAVE SOLUTIONS AND THEIR LIMITS OF A SIMPLE EQUATION
-
Abstract
In this pager, we study the elliptic singular wave solutions of the equation $ u_t+2ku_x-u_{xxt}+u^2u_x-uu_{xxx}=0 $ which has been investigated in some literatures. Firstly, for given wave speeds $ c_1=\frac{1}{2}(1+\sqrt{1-8k}) $ or $ c_2=\frac{1}{2}(1-\sqrt{1-8k}) $, we show that there exist four types of elliptic singular wave solutions, two types of elliptic sine singular wave solutions and two types of elliptic cosine singular wave solutions. Secondly, we confirm that their limits are four types of other solutions, hyperbolic smooth solitary wave solutions, hyperbolic singular wave solutions, fractional singular wave solution and trigonometric singular wave solutions. Our works extend some previous results.
-
-
References
[1] Y. Chen, W. Ye and R. Liu, The explicit periodic wave solutions and their limit forms for a generalized b-equation, Acta Mathe. Appl. Sinica, 2016, 32(2), 513–528. doi: 10.1007/s10255-016-0581-x [2] A. Daros and L. K. Arruda, On the instability of elliptic traveling wave solutions of the modified Camassa-Holm equation, J. Diff. Eqs., 2019, 266, 1946–1968. doi: 10.1016/j.jde.2018.08.017 [3] B. He, W. Rui, C. Chen, et al., Exact travelling wave solutions for a generalized Camassa-Holm equation using the integral bifurcation method, Appl. Math. Comput., 2008, 206, 141–149. [4] S. A. Khuri, New ansatz for obtaining wave solutions of the generalized Camassa-Holm equation, Chaos Solit. Fract., 2005, 25, 705–710. doi: 10.1016/j.chaos.2004.11.083 [5] J. Li and Z. Liu, Smooth and non-smooth traveling waves in a nonlinearly dispersive equation, Applied Mathematical Modelling, 2000, 25, 41–56. doi: 10.1016/S0307-904X(00)00031-7 [6] J. Li and Z. Liu, Traveling wave solutions for a class of nonlinear dispersive equations, Chin. Ann. of Math., 2002, 23B(3), 397–418. [7] Z. Li and R. Liu, Bifurcations and exact solutions in a nonlinear wave equation, Int. J. Bifurcation and Chaos, 2019, 29(7), 1950098. doi: 10.1142/S0218127419500986 [8] Z. Li and R. Liu, Blow-up solutions for a case of b-family equations, Acta Math. Scientia, 2020, 40(4), 910–920. doi: 10.1007/s10473-020-0402-4 [9] R. Liu, Coexistence of multifarious exact nonlinear wave solutions for generalized b-equation, Int. J. Bifurcation and Chaos, 2010, 20, 3193–3208. doi: 10.1142/S0218127410027623 [10] Z. Liu and Y. Liang, The explicit nonlinear wave solutions and their bifurcations of the generalized Camassa-Holm equation, Int. J. Bifurcation and Chaos, 2011, 21(11), 3119–3136. doi: 10.1142/S0218127411030556 [11] J. Shen and W. Xu, Bifurcations of smooth and non-smooth travelling wave solutions in the generalized Camassa-Holm equation, Chaos Solit. Fract., 2005, 26, 1149–1162. doi: 10.1016/j.chaos.2005.02.021 [12] L. Tian and X. Song, New peaked solitary wave solutions of the generalized Camassa-Holm equation, Chaos Solit. Fract., 2004, 21, 621–637. [13] Q. Wang and M. Tang, New exact solutions for two nonlinear equations, Phys. Lett. A, 2008, 372, 2995–3000. doi: 10.1016/j.physleta.2008.01.012 [14] A. M. Wazwaz, Solitary wave solutions for modified forms of Degasperis-Procesi and Camassa-Holm equations, Phys. Lett. A, 2006, 352, 500–504. doi: 10.1016/j.physleta.2005.12.036 [15] A. M. Wazwaz, New solitary wave solutions to the modified forms of Degasperis-Procesi and Camassa-Holm equations, Appl. Math. Comput., 2007, 186, 130–141. [16] J. Yang, R. Liu and Y. Chen, Bifurcations of solitary waves of a simple equation, Int. J. Bifurcation and Chaos, 2020, 30(9), 2050138. doi: 10.1142/S0218127420501382 [17] E. Yomba, The sub-ODE method for finding exact travelling wave solutions of generalized nonlinear Camassa-Holm, and generalized nonlinear Schrodinger equations, Phys. Lett. A, 2008, 372, 215–222. doi: 10.1016/j.physleta.2007.03.008 [18] E. Yomba, A generalized auxiliary equation method and its application to nonlinear Klein-Gordon and generalized nonlinear Camassa-Holm equations, Phys. Lett. A, 2008, 372, 1048–1060. doi: 10.1016/j.physleta.2007.09.003 -
-
Figures(6)
Export File
Citation
Zongguang Li, Zhengrong Liu. ELLIPTIC SINGULAR WAVE SOLUTIONS AND THEIR LIMITS OF A SIMPLE EQUATION[J]. Journal of Applied Analysis & Computation, 2022, 12(3): 1195-1210. doi: 10.11948/20220193
Format
Content
DownLoad:
-
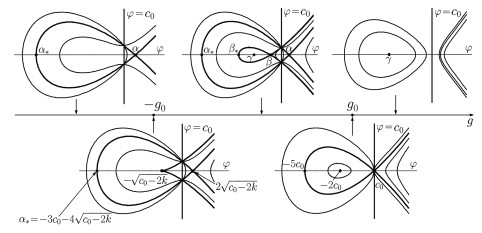
Figure 1. The bifurcation phase portraits of system (2.4) for given
$ k\leq \dfrac{1}{8} $ , and$ c_0=\dfrac{1}{2}(1\pm\sqrt{1-8k}) $ . -
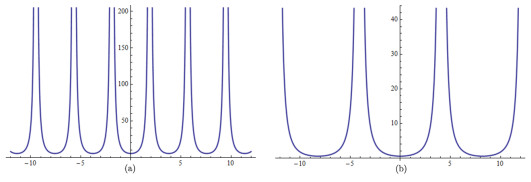
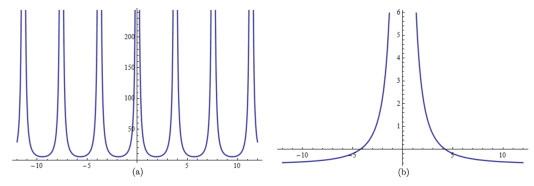
Figure 2. The evolution of wave profiles of
$ u_1(\xi, \mu) $ and$ u_2(\xi) $ , (a) that of$ u_1(\xi, \mu) $ , (b) that of$ u_2(\xi) $ . -
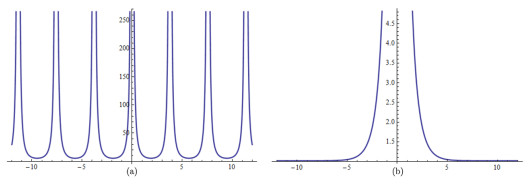
Figure 3. The evolution of wave profiles of
$ u_3(\xi, \mu) $ and$ u_4(\xi) $ , (a) that of$ u_3(\xi, \mu) $ , (b) that of$ u_4(\xi) $ . -
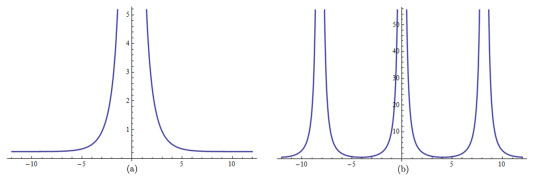
Figure 4. The evolution of wave profiles of
$ u_5(\xi) $ and$ u_6(\xi) $ , (a) that of$ u_5(\xi) $ , (b) that of$ u_6(\xi) $ . -
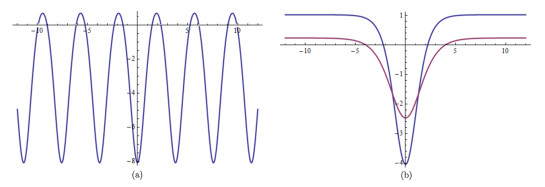
Figure 5. The evolution of wave profiles of
$ u_7(\xi, \mu) $ ,$ u_8(\xi) $ and$ u_9(\xi) $ , (a) that of$ u_7(\xi, \mu) $ , (b) that of$ u_8(\xi) $ and$ u_9(\xi) $ . -
Figure 6. The evolution of wave profiles of
$ u_{10}(\xi, \mu) $ and$ u_{11}(\xi) $ , (a) that of$ u_{10}(\xi, \mu) $ , (b) that of$ u_{11}(\xi) $ .