| Citation: |
Huizhang Yang, Wei Liu, Bin He. EVOLUTIONARY BEHAVIOR OF THE INTERACTION SOLUTIONS FOR A (3+1)-DIMENSIONAL GENERALIZED BREAKING SOLITON EQUATION[J]. Journal of Applied Analysis & Computation, 2023, 13(3): 1429-1448. doi: 10.11948/20220212
|
EVOLUTIONARY BEHAVIOR OF THE INTERACTION SOLUTIONS FOR A (3+1)-DIMENSIONAL GENERALIZED BREAKING SOLITON EQUATION
-
Abstract
The interaction solutions have attracted the attention of many scholars because of they are valuable in analyzing the nonlinear dynamics of waves in shallow water and can be used for forecasting the appearance of rogue waves. In this paper, we investigate the interaction and rational solutions of a (3+1)-dimensional generalized breaking soliton equation by employing the Hirota bilinear and parameter limit methods along with symbolic computations. By studying the Hirota bilinear form of the equation, abundant interaction and rational solutions are derived by choosing appropriate parameters of the test function. The evolutionary behavior of the interaction solutions is also analyzed theoretically and graphically. Compare with the published literatures, we get some completely new results of the equation in this paper.
-
-
References
[1] X. Cheng, W. Ma and Y. Yang, Lump-type solutions of a generalized Kadomtsev-Petviashvili equation in (3+1)-dimensions, Chin. Phys. B, 2019, 28(10), 100203. doi: 10.1088/1674-1056/ab3f20 [2] J. Gu, Y. Zhang and H. Dong, Dynamic behaviors of interaction solutions of (3+1)-dimensional Shallow Water wave equation, Comput. Math. Appl., 2018, 76(6), 1408-1419. doi: 10.1016/j.camwa.2018.06.034 [3] X. Guan, W. Liu, Q. Zhou and A. Biswas, Some lump solutions for a generalized (3+1)-dimensional Kadomtsev-Petviashvili equation, Appl. Math. Comput., 2020, 366, 124757. [4] L. Gai, W. Ma and M. Li, Lump-type solutions, rogue wave type solutions and periodic lump-stripe interaction phenomena to a (3+1)-dimensional generalized breaking soliton equation, Phys. Lett. A, 2020, 384(8), 126178. doi: 10.1016/j.physleta.2019.126178 [5] X. Hu, S. Lin and L. Wang, Integrability, multiple-cosh, lumps and lump-soliton solutions to a (2+1)-dimensional generalized breaking soliton equation, Commun. Nonlinear Sci. Numer. Simulat., 2020, 91, 105447. doi: 10.1016/j.cnsns.2020.105447 [6] K. Hosseini, A. R. Seadawy, M. Mirzazadeh, M. Eslami, S. Radmehr and D. Baleanu, Multiwave, multicomplexiton, and positive multicomplexiton solutions to a (3+1)-dimensional generalized breaking soliton equation, Alex. Eng. J., 2020, 59(5), 3473-3479. doi: 10.1016/j.aej.2020.05.027 [7] R. Hirota, The Direct Method in Soliton Theory, Springer, Berlin, 1980. [8] K. Hosseini, W. Ma, R. Ansari, M. Mirzazadeh, R. Pouyanmehr and F. Samadani, Evolutionary behavior of rational wave solutions to the (4+1)-dimensional Boiti-Leon-Manna-Pempinelli equation, Phys. Scr., 2020, 95(6), 065208. doi: 10.1088/1402-4896/ab7fee [9] B. He and Q. Meng, Bilinear form and new interaction solutions for the sixth-order Ramani equation, Appl. Math. Lett., 2019, 98, 411-418. doi: 10.1016/j.aml.2019.06.036 [10] O. A. Ilhan, J. Manafian and M. Shahriari, Lump wave solutions and the interaction phenomenon for a variable-coefficient Kadomtsev-Petviashvili equation, Comput. Math. Appl., 2019, 78, 2429-2448. doi: 10.1016/j.camwa.2019.03.048 [11] X. Liu, J. Yu and Z. Lou, New interaction solutions from residual symmetry reduction and consistent Riccati expansion of the (2+1)-dimensional Boussinesq equation, Nonlinear Dyn., 2018, 92, 1469-1479. doi: 10.1007/s11071-018-4139-8 [12] C. Liu, M. Chen, P. Zhou and L. Chen, Bi-solitons, breather solution family and rogue waves for the (2+1)-dimensional nonlinear Schrödinger equation, J. Appl. Anal. Comput., 2016, 6(2), 367-375. [13] J. Liu, W. Zhu and L. Zhou, Interaction solutions and abundant exact solutions for the new (3+1)-dimensional generalized Kadomtsev-Petviashvili equation in fluid mechanics, J. Appl. Anal. Comput., 2020, 10 (3), 960-971. [14] W. Liu, A. M. Wazwaz and X. Zheng, Families of semi-rational solutions to the Kadomtsev-Petviashvili I equation, Commun. Nonlinear Sci. Numer. Simulat., 2019, 67, 480-491. doi: 10.1016/j.cnsns.2018.07.020 [15] J. Liu, J. Du, Z. Zeng and B. Nie, New three-wave solutions for the (3+1)-dimensional Boiti-Leon-Manna-Pempinelli equation, Nonlinear Dyn., 2017, 88, 655-661. doi: 10.1007/s11071-016-3267-2 [16] Z. Li, J. Manafian, N. Ibrahimov, A. Hajar, K. S. Nisar and W. Jamshed, Variety interaction between k-lump and k-kink solutions for the generalized Burgers equation with variable coefficients by bilinear analysis, Results Phys., 2021, 28, 104490. doi: 10.1016/j.rinp.2021.104490 [17] W. Ma, A search for lump solutions to a combined fourth-order nonlinear PDE in (2+1)-dimensions, J. Appl. Anal. Comput., 2019, 9(4), 1319-1332. [18] J. Manafian, S. A. Mohammed, A. Alizadeh, H. M. Baskonus and W. Gao, Investigating lump and its interaction for the third-order evolution equation arising propagation of long waves over shallow water, Eur. J. Mech. B-Fluid., 2020, 84, 289-301. doi: 10.1016/j.euromechflu.2020.04.013 [19] J. Manafian and M. Lakestani, N-lump and interaction solutions of localized waves to the (2+1)-dimensional variable-coefficient Caudrey-Dodd-Gibbon-Kotera-Sawada equation, J. Geom. Phys., 2020, 150, 103598. doi: 10.1016/j.geomphys.2020.103598 [20] J. Manafian, B. Mohammadi-Ivatloo and M. Abapour, Lump-type solutions and interaction phenomenon to the (2+1)-dimensional Breaking Soliton equation, Appl. Math. Comput., 2019, 356, 13-41. [21] Y. Ma and B. Li, Interactions between soliton and rogue wave for a (2+1)-dimensional generalized breaking soliton system: Hidden rogue wave and hidden soliton, Comput. Math. Appl., 2019, 78 (3), 827-839. doi: 10.1016/j.camwa.2019.03.002 [22] Q. Meng, Rational solutions and interaction solutions for a fourth-order nonlinear generalized Boussinesq water wave equation, Appl. Math. Lett., 2020, 110, 106580. doi: 10.1016/j.aml.2020.106580 [23] Y. Qian, J. Manafian, S. Y. Mohyaldeen, L. S. Esmail, S. A. Gorovoy and G. Singh, Multiple-order line rogue wave, lump and its interaction, periodic, and cross-kink solutions for the generalized CHKP equation, Propuls. Power Res., 2021, 10(3), 277-293. doi: 10.1016/j.jppr.2021.09.002 [24] B. Ren, W. Ma and J. Yu, Rational solutions and their interaction solutions of the (2+1)-dimensional modified dispersive water wave equation, Comput. Math. Appl., 2019, 77 (8), 2086-2095. doi: 10.1016/j.camwa.2018.12.010 [25] G. Shen, J. Manafian, D. T. N. Huy, K. S. Nisar, M. Abotaleb and N. D. Trung, Abundant soliton wave solutions and the linear superposition principle for generalized (3+1)-D nonlinear wave equation in liquid with gas bubbles by bilinear analysis, Results Phys., 2022, 32, 105066. doi: 10.1016/j.rinp.2021.105066 [26] W. Tan, Z. Dai, J. Xie and D. Qiu, Parameter limit method and its application in the (4+1)-dimensional Fokas equation, Comput. Math. Appl., 2018, 75 (12), 4214-4220. doi: 10.1016/j.camwa.2018.03.023 [27] W. Tan, W. Zhang and J. Zhang, Evolutionary behavior of breathers and interaction solutions with M-solitons for (2+1)-dimensional KdV system, Appl. Math. Lett., 2020, 101, 106063. doi: 10.1016/j.aml.2019.106063 [28] S. Tian, D. Guo, X. Wang and T. Zhang, Traveling wave, lump wave, rogue wave, multi-kink solitary wave and interaction solutions in a (3+1)-dimensional Kadomtsev-Petviashvili equation with Bäcklund transformation, J. Appl. Anal. Comput., 2021, 11(1), 45-58. [29] J. Wu, Y. Liu, L. Piao, J. Zhuang and D. Wang, Nonlinear localized waves resonance and interaction solutions of the (3+1)-dimensional Boiti-Leon-Manna-Pempinelli equation, Nonlinear Dyn., 2020, 100, 1527-1541. doi: 10.1007/s11071-020-05573-y [30] A. M. Wazwaz, A new integrable (2+1)-dimensional generalized breaking soliton equation: n-soliton solutions and traveling wave solutions, Commun. Theor. Phys., 2016, 66(4), 385-388. doi: 10.1088/0253-6102/66/4/385 [31] G. Xu, Integrability of a (2+1)-dimensional generalized breaking soliton equation, Appl. Math. Lett., 2015, 50, 16-22. [32] Y. Xu, X. Zheng and J. Xin, Abundant new non-traveling wave solutions for the (3+1)-dimensional Boiti-Leon-Manna-Pempinelli equation, J. Appl. Anal. Comput., 2021, 11(4), 2052-2069. [33] Y. Yin, W. Ma, J. Liu and X. Lü, Diversity of exact solutions to a (3+1)-dimensional nonlinear evolution equation and its reduction, Comput. Math. Appl., 2018, 76(6), 1275-1283. [34] X. Yan, S. Tian, M. Dong, L. Zhou and T. Zhang, Characteristics of solitary wave, homoclinic breather wave and rogue wave solutions in a (2+1)-dimensional generalized breaking soliton equation, Comput. Math. Appl., 2018, 76(1), 179-186. [35] Y. Zhou, S. Manukure and W. Ma, Lump and lump-soliton solutions to the Hirota-Satsuma-Ito equation, Commun. Nonlinear Sci. Numer. Simulat., 2019, 68, 56-62. [36] Z. Zhao and B. Han, Quasiperiodic wave solutions of a (2+1)-dimensional generalized breaking soliton equation via bilinear Bäcklund transformation, Eur. Phys. J. Plus, 2016, 131, 128. -
-
Figures(19)
Export File
Citation
Huizhang Yang, Wei Liu, Bin He. EVOLUTIONARY BEHAVIOR OF THE INTERACTION SOLUTIONS FOR A (3+1)-DIMENSIONAL GENERALIZED BREAKING SOLITON EQUATION[J]. Journal of Applied Analysis & Computation, 2023, 13(3): 1429-1448. doi: 10.11948/20220212
Format
Content
DownLoad:
-
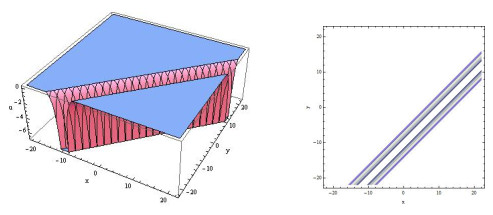
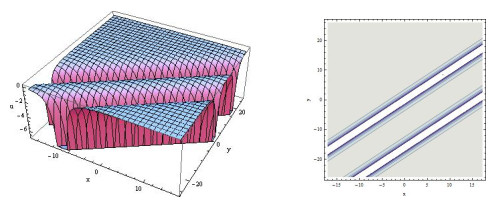
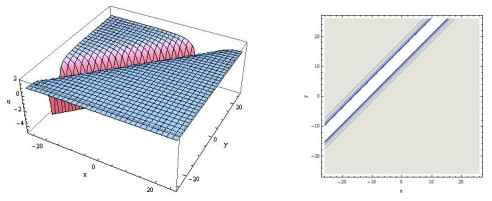
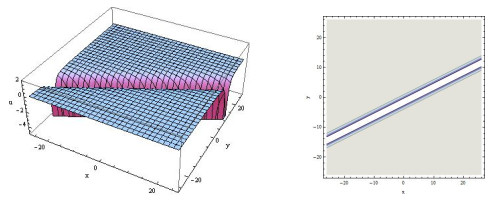
Figure 1.
Three-dimensional and contour plots of (3.8).
-
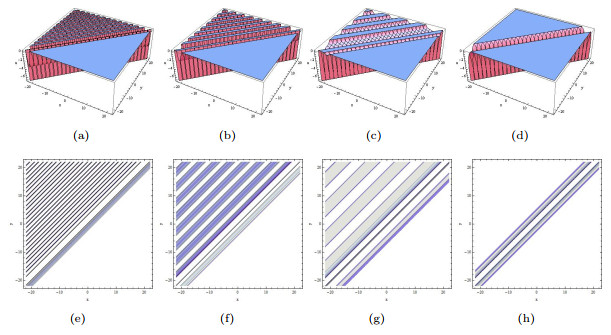
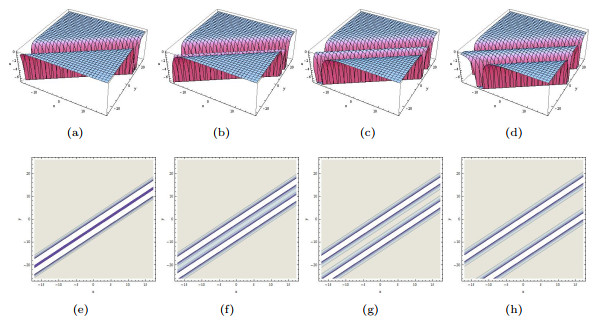
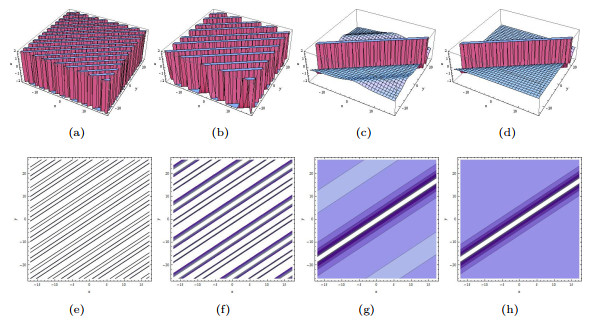
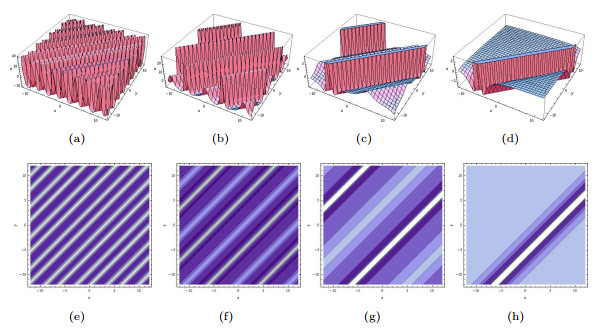
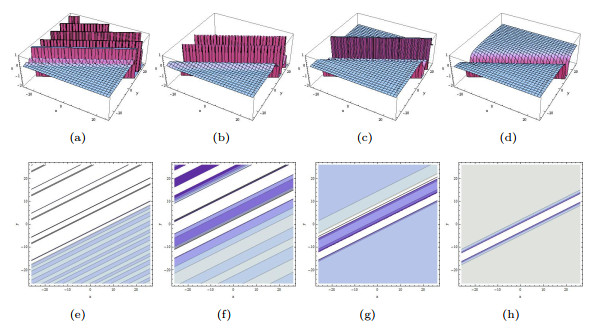
Figure 2.
The limiting precess of (3.7) tends to (3.8) when
$ p_1\rightarrow0. $ $ p_1=1, p_2=1, a_2=\cos(1) $ $ p_1=0.6, p_2=0.6, a_2=\cos(0.6) $ $ p_1=0.3, p_2=0.3, a_2=\cos(0.3) $ $ p_1=0.01, p_2=0.01, a_2=\cos(0.01) $ -
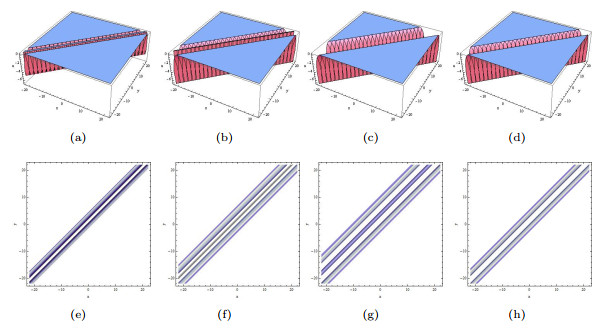
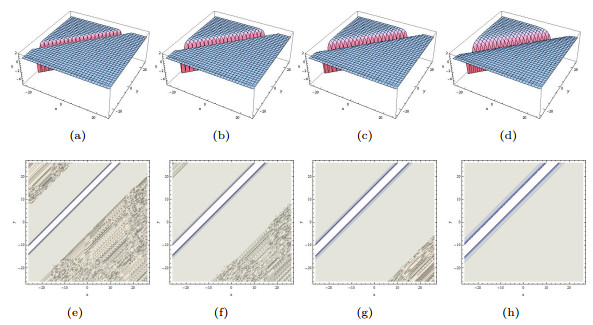
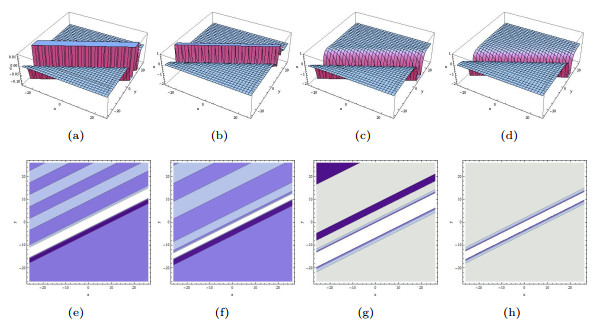
Figure 3.
The limiting precess of (3.9) tends to (3.8) when
$ p_1\rightarrow0. $ $ p_1=0.6, \bar{p}_2=0.6, a_2=\cosh(0.6) $ $ p_1=0.2, \bar{p}_2=0.2, a_2=\cosh(0.2) $ $ p_1=0.07, \bar{p}_2=0.07, a_2=\cosh(0.07) $ $ p_1=0.001, \bar{p}_2=0.001, a_2=\cosh(0.001) $ -
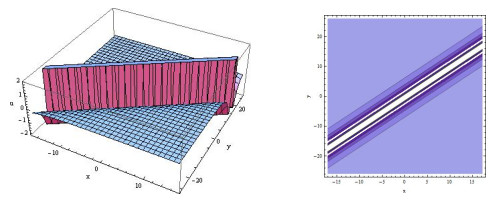
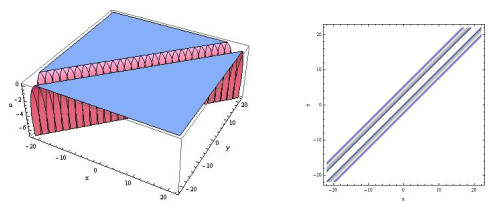
Figure 4.
Three-dimensional and contour plots of (3.11).
-
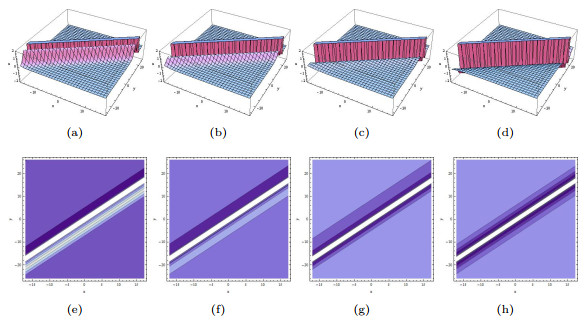
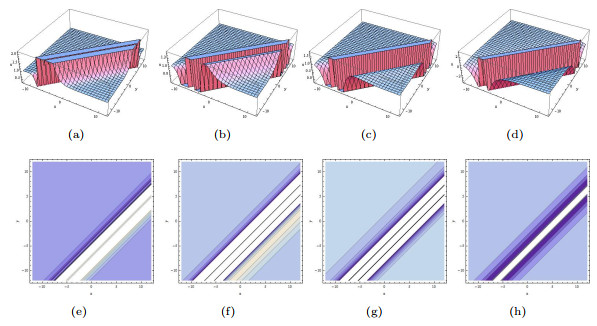
Figure 5.
The limiting precess of (3.10) tends to (3.11) when
$ p_1\rightarrow0. $ $ p_1=1, p_2=1, a_2=\cos(1) $ $ p_1=0.7, p_2=0.7, a_2=\cos(0.7) $ $ p_1=0.5, p_2=0.5, a_2=\cos(0.5) $ $ p_1=0.05, p_2=0.05, a_2=\cos(0.05) $ -
Figure 6.
Three-dimensional and contour plots of (3.13).
-
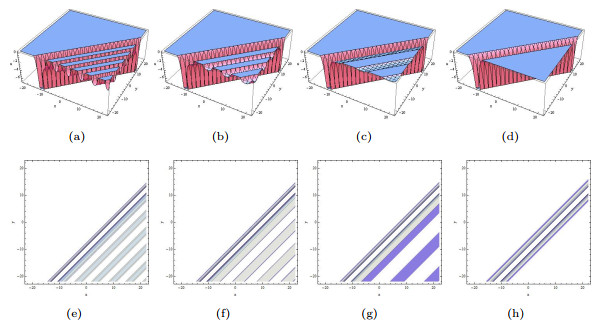
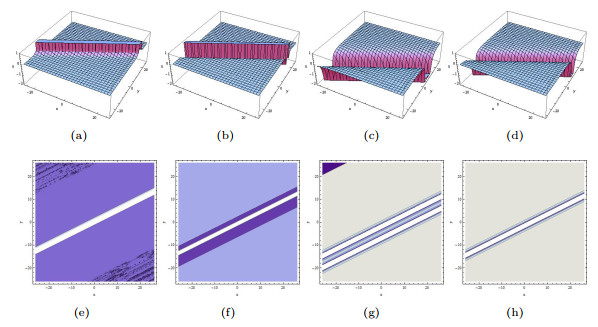
Figure 7.
The limiting precess of (3.12) tends to (3.13) when
$ p_2\rightarrow0. $ $ p_2=0.35, p_3=0.35, a_2=\cos(0.35), a_3=\cosh(0.35) $ $ p_2=0.22, p_3=0.22, a_2=\cos(0.22), a_3=\cosh(0.22) $ $ p_2=0.12, p_3=0.12, a_2=\cos(0.12), a_3=\cosh(0.12) $ $ p_2=0.01, p_3=0.01, a_2=\cos(0.01), a_3=\cosh(0.01) $ -
Figure 8.
Three-dimensional and contour plots of (3.15).
-
Figure 9.
The limiting precess of (3.14) tends to (3.15) when
$ \bar{p}_2\rightarrow0. $ $ \bar{p}_2=0.77, p_3=0.77, a_2=\cosh(0.77), a_3=\cosh(0.77) $ $ \bar{p}_2=0.6, p_3=0.6, a_2=\cosh(0.6), a_3=\cosh(0.6) $ $ \bar{p}_2=0.4, p_3=0.4, a_2=\cosh(0.4), a_3=\cosh(0.4) $ $ \bar{p}_2=0.02, p_3=0.02, a_2=\cosh(0.02), a_3=\cosh(0.02) $ -
Figure 10.
The limiting precess of (3.16) tends to (3.15) when
$ p_2\rightarrow0. $ $ p_2=0.7, \bar{p}_3=0.7, a_2=\cos(0.7), a_3=\cos(0.7) $ $ p_2=0.4, \bar{p}_3=0.4, a_2=\cos(0.4), a_3=\cos(0.4) $ $ p_2=0.12, \bar{p}_3=0.12, a_2=\cos(0.12), a_3=\cos(0.12) $ $ p_2=0.02, \bar{p}_3=0.02, a_2=\cos(0.02), a_3=\cos(0.02) $ -
Figure 11.
Three-dimensional and contour plots of (3.18).
-
Figure 12.
The limiting precess of (3.17) tends to (3.18) when
$ p_2\rightarrow0. $ $ p_2=1, p_3=1, a_2=\cos(1), a_3=\cosh(1) $ $ p_2=0.6, p_3=0.6, a_2=\cos(0.6), a_3=\cosh(0.6) $ $ p_2=0.4, p_3=0.4, a_2=\cos(0.4), a_3=\cosh(0.4) $ $ p_2=0.04, p_3=0.04, a_2=\cos(0.04), a_3=\cosh(0.04) $ -
Figure 13.
Three-dimensional and contour plots of (3.20).
-
Figure 14.
The limiting precess of (3.19) tends to (3.20) when
$ \bar{p}_2\rightarrow0. $ $ \bar{p}_2=1, p_3=1, a_2=\cosh(1), a_3=\cosh(1) $ $ \bar{p}_2=0.6, p_3=0.6, a_2=\cosh(0.6), a_3=\cosh(0.6) $ $ \bar{p}_2=0.45, p_3=0.45, a_2=\cosh(0.45), a_3=\cosh(0.45) $ $ \bar{p}_2=0.05, p_3=0.05, a_2=\cosh(0.05), a_3=\cosh(0.05) $ -
Figure 15.
The limiting precess of (3.21) tends to (3.20) when
$ p_2\rightarrow0. $ $ p_2=1, \bar{p}_3=1, a_2=\cos(1), a_3=\cos(1) $ $ p_2=0.6, \bar{p}_3=0.6, a_2=\cos(0.6), a_3=\cos(0.6) $ $ p_2=0.3, \bar{p}_3=0.3, a_2=\cos(0.3), a_3=\cos(0.3) $ $ p_2=0.05, \bar{p}_3=0.05, a_2=\cos(0.05), a_3=\cos(0.05) $ -
Figure 16.
Three-dimensional and contour plots of (3.23).
-
Figure 17.
The limiting precess of (3.22) tends to (3.23) when
$ p_1\rightarrow0. $ $ p_1=0.15, p_2=0.15, p_3=0.15, a_2=\cos(0.15), a_3=\cosh(0.15) $ $ p_1=0.1, p_2=0.1, p_3=0.1, a_2=\cos(0.1), a_3=\cosh(0.1) $ $ p_1=0.05, p_2=0.05, p_3=0.05, a_2=\cos(0.05), a_3=\cosh(0.05) $ $ p_1=0.001, p_2=0.001, p_3=0.001, a_2=\cos(0.001), a_3=\cosh(0.001) $ -
Figure 18.
The limiting precess of (3.24) tends to (3.23) when
$ p_1\rightarrow0. $ $ p_1=0.7, \bar{p}_2=0.7, p_3=0.7, a_2=\cosh(0.7), a_3=\cosh(0.7) $ $ p_1=0.2, \bar{p}_2=0.2, p_3=0.2, a_2=\cosh(0.2), a_3=\cosh(0.2) $ $ p_1=0.02, \bar{p}_2=0.02, p_3=0.02, a_2=\cosh(0.02), a_3=\cosh(0.02) $ $ p_1=0.001, \bar{p}_2=0.001, p_3=0.001, a_2=\cosh(0.001), a_3=\cosh(0.001) $ -
Figure 19.
The limiting precess of (3.25) tends to (3.23) when
$ p_1\rightarrow0. $ $ p_1=0.3, p_2=0.3, \bar{p}_3=0.3, a_2=\cos(0.3), a_3=\cos(0.3) $ $ p_1=0.1, p_2=0.1, \bar{p}_3=0.1, a_2=\cos(0.1), a_3=\cos(0.1) $ $ p_1=0.02, p_2=0.02, \bar{p}_3=0.02, a_2=\cos(0.02), a_3=\cos(0.02) $ $ p_1=0.001, p_2=0.001, \bar{p}_3=0.001, a_2=\cos(0.001), a_3=\cos(0.001) $