| Citation: | N. Ghanbari, K. Sayevand, I. Masti. A RELIABLE APPROACH FOR ANALYSING THE NONLINEAR KDV EQUATION OF FRACTIONAL ORDER[J]. Journal of Applied Analysis & Computation, 2023, 13(3): 1449-1474. doi: 10.11948/20220317 |
A RELIABLE APPROACH FOR ANALYSING THE NONLINEAR KDV EQUATION OF FRACTIONAL ORDER
-
Abstract
Its applications in many domains, along with its challenging analytical solution, have led to several studies of the Korteweg-de Vries (KdV) equation over the past decade. Due to difficulties or impossibility with the analytical solution to this equation, the paper presents a numerical solution using the Crank-Nicolson difference method. A study of the stability and solvency of this method has been undertaken. In this paper, we prove that the scheme is first order convergent in space and $\min \{ 2 - \nu , r\nu \} $ order convergent in time, where $ r$ refers to a gradation parameter and $\nu$ represents the fractional derivative. The results are then presented in numerical applications, looking at how it compares with other sophisticated schemes in the literature. The main benefit of the proposed scheme is the efficiency with regard to accuracy as compared to other available schemes.
-

-
References
[1] M. Abbaszadeh and M. Dehghan, The Crank-Nicolson/interpolating stabilized element-free Galerkin method to investigate the fractional Galilei invariant advection‐diffusion equation, Mathematical Methods in the Applied Sciences, 2021, 44(4), 2752-2768. doi: 10.1002/mma.5871 [2] A. Babaei and S. Banihashemi, Reconstructing unknown nonlinear boundary conditions in a time‐fractional inverse reaction-diffusion-convection problem, Numerical Methods for Partial Differential Equations, 2019, 35(3), 976-992. doi: 10.1002/num.22334 [3] A. Babaei and S. Banihashemi, Stable numerical approach to solve a time-fractional inverse heat conduction problem, Iranian Journal of Science and Technology, Transactions A: Science, 2018, 42(4), 2225-2236. doi: 10.1007/s40995-017-0360-4 [4] A. Babaei, H. Jafari, S. Banihashemi and M. Ahmadi, Mathematical analysis of a stochastic model for spread of Coronavirus, Chaos, Solitons and Fractals, 2021, 145, 110788. doi: 10.1016/j.chaos.2021.110788 [5] D. Baleanu, K. Diethelm, E. Scalas and J. J. Trujillo, Fractional calculus: models and numerical methods, World Scientific, Singapore, 2012. [6] D. Baleanu and B. Shiri, Nonlinear higher order fractional terminal value problems, AIMS Mathematics, 2022, 7(5), 7489-7506. doi: 10.3934/math.2022420 [7] E. F. Browder, Existence and uniqueness theorems for solutions of nonlinear boundary value problems, Proceedings of the Symposia in Applied Mathematics, Providence, AMS, 1965, 1724-29. [8] H. Brunner, The numerical solution of weakly singular Volterra integral equations by collocation on graded meshes, Mathematics Computation, 1985, 45, 417-437. doi: 10.1090/S0025-5718-1985-0804933-3 [9] H. Brunner, L. Ling and M. Yamamoto, Numerical simulations of 2D fractional subdiffusion problems, Journal of Computational Physics, 2010, 229, 6613-6622. doi: 10.1016/j.jcp.2010.05.015 [10] W. Cao, Y. Xu and Z. Zheng, Finite difference/collocation method for a generalized time-fractional KdV equation, Applied Sciences, 2018, 8(1), 42, https://doi.org/10.3390/app8010042. doi: 10.3390/app8010042 [11] A. El-Ajou, O. A. Arqub and S. Momani, Approximate analytical solution of the nonlinear fractional KdV-Burgers equation: A new iterative algorithm, Journal of Computational Physics, 2015, 293, 81-95. doi: 10.1016/j.jcp.2014.08.004 [12] R. Erfanifar, K. Sayevand, N. Ghanbari and H. Esmaeili, A modified Chebyshev ϑ-weighted Crank-Nicolson method for analyzing fractional sub-diffusion equations, Numerical Methods for Partial Differential Equations, 2021, 37(1), 614-625. doi: 10.1002/num.22543 [13] R. M. Ganji, H. Jafari, S. P. Moshokoa and N. S. Nkomo, A mathematical model and numerical solution for brain tumor derived using fractional operator, Results in Physics, 2021, 28, 104671. doi: 10.1016/j.rinp.2021.104671 [14] S. Jiang, J. Zhang, Q. Zhang and Z. Zhang, Fast evalution of the caputo fractional derivative and its applications to fractional diffusion equations, Communications in Computational Physics, 2017, 21, 650-678. doi: 10.4208/cicp.OA-2016-0136 [15] D. J. Kordeweg and G. Vries, On the change of form of long waves advancing in a rectangular channel, and a new type of long stationary wave, Philosophical Magazine, 1895, 39, 422-443. [16] C. Li and M. Cai, Theory and numerical approximations of fractional integrals and derivatives, Society for Industrial and Applied Mathematics, 2019, https://doi.org/10.1137/1.9781611975888. doi: 10.1137/1.9781611975888 [17] H. Liao, D. Li and J. Zhang, Sharp error estimate of the nonuniform l1 formula for linear reaction-subdiffusion equations, SIAM Journal on Numerical Analysis, 2018, 56(2), 1112-1133. doi: 10.1137/17M1131829 [18] N. H. Luc, H. Jafari and P. Kumam, On an initial value problem for time fractional pseudo-parabolic equation with Caputo derivarive, Mathematical Methods in the Applied Sciences, 2021, https://doi.org/10.1002/mma.7204. doi: 10.1002/mma.7204 [19] S. Momani, An explicit and numerical solutions of the fractional KdV equation, Mathematics and Computer in Simulation, 2005, 70(2), 110-118. doi: 10.1016/j.matcom.2005.05.001 [20] K. Mustapha, An implicit finite difference time-stepping method for a subdiffusion equation with spatial discretization by finite elements, IMA Journal of Numerical Analysis, 2011, 31, 719-739. doi: 10.1093/imanum/drp057 [21] M. Sajjadian, Numerical solutions of Korteweg de Vries and Korteweg de Vries-Burger's equations using computer programming, International Journal of Nonlinear Science, 2013, 15(1), 69-79. [22] K. Sayevand, N. Ghanbari and I. Masti, A robust computational framework for analyzing the Bloch-Torrey equation of fractional order, Computational and Applied Mathematics, 2021, 40(4), 1-21. [23] K. Sayevand, J. T. Machado and I. Masti, Analysis of dual Bernstein operators in the solution of the fractional convection-diffusion equation arising in underground water pollution, Journal of Computational and Applied Mathematics, 2022, 399, 113729. doi: 10.1016/j.cam.2021.113729 [24] K. Sayevand, J. T. Machado and I. Masti, On dual Bernstein polynomials and stochastic fractional integro-differential equations, Mathematical Methods in the Applied Sciences, 2020, 43(17), 9928-9947. doi: 10.1002/mma.6667 [25] Y. Shen, Z. Sun and R. Du, Fast finite difference schemes for the time-fractional diffusion equations with a weak singularity at the initial time, East Asian Journal on Applied Mathematics, 2018, 8(4), 834-858. doi: 10.4208/eajam.010418.020718 [26] J. Shen, Z. Sun and W. Cao, A finite difference scheme on graded meshes for time-fractional nonlinear Korteweg-de Vries equation, Applied Mathematics and Computation, 2019, 361, 752-765. doi: 10.1016/j.amc.2019.06.023 [27] A. Shidfar and A. Babaei, The Sinc-Galerkin method for solving an inverse parabolic problem with unknown source term, Numerical Methods for Partial Differential Equations, 2013, 29, 64-78. doi: 10.1002/num.21699 [28] M. Stynes, E. ORiordan and J. L. Gracia, Error analysis of a finite difference method on graded meshes for a time-fractional diffusion equation, SIAM Journal on Numerical Analysis, 2015, 55(2), 1057-1079. [29] H. Sun and Z. Sun, On two linearized difference schemes for burgers equation, International Journal of Computer Mathematics, 2015, 92(6), 1160-1179. doi: 10.1080/00207160.2014.927059 [30] A. Taghavi, A. Babaei and A. Mohammadpour, A stable numerical scheme for a time-fractional inverse parabolic equation, Inverse Problems in Science and Engineering, 2017, 25(10), 1474-1491. doi: 10.1080/17415977.2016.1267169 [31] Q. Wang, Numerical solutions for fractional KdV-Burgers equation by Adomian decomposition method, Applied Mathematics and Computation, 2006, 182, 1048-1055. doi: 10.1016/j.amc.2006.05.004 [32] Y. Zhang, Z. Sun and H. Liao, Finite difference methods for the time fractional diffusion equation on nonuniform meshes, Journal of Computational Physics, 2014, 265, 195-210. doi: 10.1016/j.jcp.2014.02.008 -
-
-
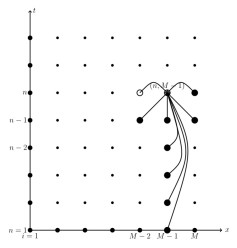
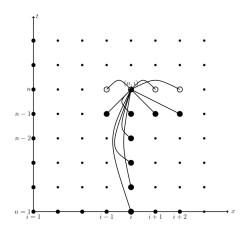
Figure 1.
when
$ 1\leq j \leq \mathcal{M}-2, \;\; 1\leq n \leq \mathcal{N} $ -
Figure 2.
when
$ j=\mathcal{M}-1, \;\; 1\leq n \leq \mathcal{N} $ -
Figure 3.
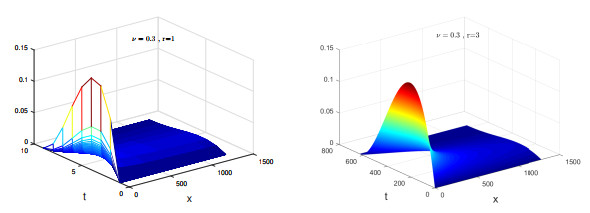
The numerical solutions of Example 7.2 for
$ \nu = 0.3, r = 1 $ $ \nu = 0.3, r = 3 $ -
Figure 4.
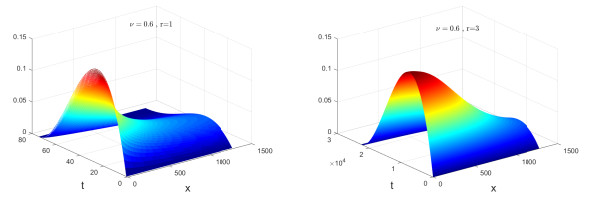
The numerical solutions of Example 7.2 for
$ \nu = 0.6, r = 1 $ $ \nu = 0.6, r = 3 $ -
Figure 5.
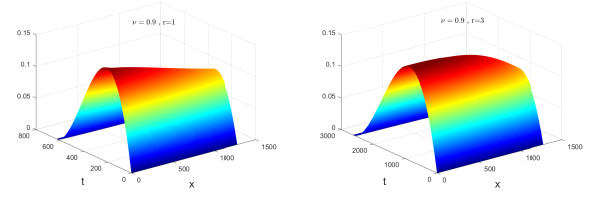
The numerical solutions of Example 7.2 for
$ \nu = 0.9, r = 1 $ $ \nu = 0.9, r = 3 $




 DownLoad:
DownLoad: