| Citation: | Lihua Dai, Zhouhong Li. ALMOST PERIODIC SYNCHRONIZATION FOR COMPLEX-VALUED NEURAL NETWORKS WITH TIME-VARYING DELAYS AND IMPULSIVE EFFECTS ON TIME SCALES[J]. Journal of Applied Analysis & Computation, 2023, 13(2): 893-912. doi: 10.11948/20220214 |
ALMOST PERIODIC SYNCHRONIZATION FOR COMPLEX-VALUED NEURAL NETWORKS WITH TIME-VARYING DELAYS AND IMPULSIVE EFFECTS ON TIME SCALES
-
Abstract
We propose a class of complex-valued neural networks with time-varying delays and impulsive effects on time scales. By employing the Banach fixed point theorem and differential inequality technique on time scales, we obtain the existence of almost periodic solutions for this networks. Then, by constructing a suitable Lyapunov function, we obtain that the drive-response structure of complex-valued neural networks with almost periodic coefficients can realize the global exponential synchronization. Our results are completely new. Finally, we give an example to illustrate the feasibility of our results.
-
Keywords:
- Complex-valued neural networks /
- synchronization /
- impulsive effects /
- time scales
-

-
References
[1] I. Aizenberg, Complex-valued neural networks with multi-valued neurons, Heidelberg, Springer, 2011. [2] M. Ali and J. Yogambigai, Synchronization criterion of complex dynamical networks with both leakage delay and coupling delay on time scales, Neural Process. Lett., 2019, 49(2), 453-466. doi: 10.1007/s11063-018-9821-9 [3] M. Bohner and A. Peterson, Dynamic Equations on Time Scales, An Introduction with Applications, Birkhäuser, Boston, 2001. [4] M. Bohner and A. Peterson, Advances in Dynamic Equations on Time Scales, Birkhäuser, Boston, 2003. [5] M. Bohner, V. S. H. Rao and S. Sanyal, Global stability of complex-valued neural networks on time scales, Differ. Equ. Dyn. Syst., 2011, 19(1-2), 3-11. doi: 10.1007/s12591-010-0076-9 [6] X. Chen, Z. Zhao, Q. Song and J. Hu, Multistability of complex-valued neural networks with time-varying delays, Appl. Math. Comput., 2017, 294, 18-35. [7] X. Chen and Q. Song, Global stability of complex-valued neural networks with both leakage time delay and discrete time delay on times cales, Neurocomputing, 2013, 121, 254-264. doi: 10.1016/j.neucom.2013.04.040 [8] Q. Cheng and J. Cao, Synchronization of complex dynamical networks with discrete time delays on time scales, Neurocomputing, 2015, 151, 729-736. doi: 10.1016/j.neucom.2014.10.033 [9] L. Duan, L. Huang and X. Fang, Finite-time synchronization for recurrent neural networks with discontinuous activations and time-varying delays, Chaos, 2017, 27(1), 013101. doi: 10.1063/1.4966177 [10] B. Du, Y. Liu, H. Batarfi and F. Alsaadi, Almost periodic solution for a neutral-type neural networks with distributed leakage delays on time scales, Neurocomputing, 2016, 173(P3), 921-929. [11] T. Fang and J. Sun, Stability of complex-valued recurrent neural networks with time-delays, IEEE Trans. Neural Netw. Learn. Syst., 2014, 25(9), 1709-1713. doi: 10.1109/TNNLS.2013.2294638 [12] S. Guo, Song and B. Du, Global exponential stability of periodic solution for neutral-type complex-valued neural networks, Discrete Dyn. Nat. Soc., 2016. DOI10.1155/2016/1267954. doi: 10.1155/2016/1267954 [13] J. Gao, Q. Wang and L. Zhang, Existence and stability of almost-periodic solutions for cellular neural networks with time-varying delays in leakage terms on time scales, Appl. Math. Comput., 2014, 237, 639-649. [14] A. Hirose, Complex-Valued Neural Networks: Theories and Applications, World Scientific, 2003. [15] J. Hu and J. Wang, Global stability of complex-valued recurrent neural networks with time-delays, IEEE Trans. Neural Netw. Learn. Syst., 2012, 23(6), 853-865. doi: 10.1109/TNNLS.2012.2195028 [16] X. Huang and J. Cao, Generalized synchronization for delayed chaotic neural networks: a novel coupling scheme, Nonlinearity, 2006, 19(12), 2797-2811. doi: 10.1088/0951-7715/19/12/004 [17] W. He and J. Cao, Exponential synchronization of chaotic neural networks: a matrix measure approach, Nonlinear Dynam., 2009, 55(1-2), 55-65. doi: 10.1007/s11071-008-9344-4 [18] S. Hilger, Analysis on measure chains-a unified approach to continuous and discrete calculus, Results Math., 1990, 18(1-2), 18-56. doi: 10.1007/BF03323153 [19] Z. Huang, H. Bin, J. Cao and B. Wang, Synchronizing neural networks with proportional delays based on a class of $q$-Type allowable time scales, IEEE Trans. Neural Netw. Learn. Syst., 2107, 99, 1-11. [20] J. Jian and P. Wan, Global exponential convergence of fuzzy complex-valued neural networks with time-varying delays and impulsive effects, Fuzzy Set. Syst., 2018, 338, 23-39. doi: 10.1016/j.fss.2017.12.001 [21] H. Jafari, A. Haghbin, S. Johnston and D. Baleanu, A new algorithm for solving dynamic equations on a time scale, J. Comput. Appl. Math., 2017, 312, 167-173. doi: 10.1016/j.cam.2016.02.047 [22] Y. Kan, J. Lu, J. Qiu and J. Kurths, Exponential synchronization of time-varying delayed complex-valued neural networks under hybrid impulsive controllers, Neural Netw., 2019, 114, 157-163. doi: 10.1016/j.neunet.2019.02.006 [23] V. Lakshmikantham, D. Bainov and P. Simeonov, Theory of Impulsive Differential Equations, World Scientific, Singapore, New Jersey, London, 1989. [24] Y. Li and C. Li, Matrix measure strategies for stabilization and synchronization of delayed BAM neural networks, Nonlinear Dynam., 2016, 84(3), 1759-1770. doi: 10.1007/s11071-016-2603-x [25] X. Lu, X. Zhang and Q. Liu, Finite-time synchronization of nonlinear complex dynamical networks on time scales via pinning impulsive control, Neurocomputing, 2108, 275, 2104-2110. [26] L. Li, X. Shi and J. Liang, Synchronization of impulsive coupled complex-valued neural networks with delay: The matrix measure method, Neural Netw., 2019, 117, 285-294. doi: 10.1016/j.neunet.2019.05.024 [27] Y. Li and C. Wang, Almost periodic functions on time scales and applications, Discrete Dyn. Nat. Soc., 2011. DOI10.1155/2011/727068. doi: 10.1155/2011/727068 [28] Y. Li and C. Wang, Uniformly almost periodic functions and almost periodic solutions to dynamic equations on time scales, Abstr. Appl. Anal., 2011. DOI: 10.1155/2011/341520. [29] X. Liu and K. Zhang, Synchronization of linear dynamical networks on time scales: pinning control via delayed impulses, Automatica, 2106, 72, 147-152. [30] X. Lu, Y. Wang and Y. Zhao, Synchronization of complex dynamical networks on time scales via Wirtinger-based inequality, Neurocomputing, 2016, 216, 143-149. doi: 10.1016/j.neucom.2016.07.031 [31] V. Mil'man and A. Myškis, On the stability of motion in the presence of impulses, Sibirsk. Mat., 1960, 1(2), 233-237. [32] J. Pan, X. Liu and W. Xie, Exponential stability of a class of complex-valued neural networks with time-varying delays, Neurocomputing, 2015, 164, 293-299. doi: 10.1016/j.neucom.2015.02.024 [33] R. Rakkiyappan, G. Velmurugan and X. Li, Complete stability analysis of complex-valued neural networks with time delays and impulses, Neural Process. Lett., 2105, 41(3), 435-468. [34] K. Subramanian and P. Muthukumar, Global asymptotic stability of complex-valued neural networks with additive time-varying delays, Cogn. Neurodyn, 2017, 11(3), 293-306. doi: 10.1007/s11571-017-9429-1 [35] G. Stamov and I. Stamova, Almost periodic solutions for impulsive neural networks with delay, Appl. Math. Model., 2007, 31(7), 1263-1270. doi: 10.1016/j.apm.2006.04.008 [36] G. Stamov, Almost periodic solutions of impulsive differential equations, Lecture Notes in Mathematics, Springer, Heidelberg, Germany, 2012. [37] Q. Song, H. Yan, Z. Zhao and Y. Liu, Global exponential stability of complex-valued neural networks with both time-varying delays and impulsive effects, Neural Netw., 2106, 79, 108-116. [38] Q. Song, H. Yan, Z. Zhao and Y. Liu, Global exponential stability of impulsive complex-valued neural networks with both asynchronous time-varying and continuously distributed delays, Neural Netw., 2016, 81, 1-10. doi: 10.1016/j.neunet.2016.04.012 [39] Q. Song and Z. Zhao, Stability criterion of complex-valued neural networks with both leakage delay and time-varying delays on time scales, Neurocomputing, 2016, 171, 179-184. doi: 10.1016/j.neucom.2015.06.032 [40] Y. Tan and Z. Huang, Synchronization of drive-response networks with delays on time scales, IEEE/CAA J. Autom. Sin., 2016, 99, 1-10. [41] Z. Wang and X. Liu, Exponential stability of impulsive complex-valued neural networks with time delay, Math. Comput. Simulation, 2019, 156, 143-157. doi: 10.1016/j.matcom.2018.07.006 [42] P. Wang, Y. Li and Y. Ye, Almost periodic solutions for neutral-type neural networks with the delays in the leakage term on time scales, Math. Methods Appl. Sci., 2016, 39, 4297-4310. doi: 10.1002/mma.3857 [43] P. Wang, The comparison theorems of dynamic equations on time scales and its applications, Ph. D. thesis, Yunnan University, 2015. [44] X. Xu, J. Zhang and J. Shi, Dynamical behaviour analysis of delayed complex-valued neural networks with impulsive effect, Internat. J. Systems Sci., 2017, 48(4), 686-694. doi: 10.1080/00207721.2016.1206988 [45] Y. Xu, R. Shen and W. Li, Finite-time synchronization for coupled systems with time delay and stochastic disturbance under feedback control, J. Appl. Anal. Comput., 2020, 10(1), 1-24. [46] C. Xu, P. Li and Y. Pang, Existence and global exponential stability of almost periodic solutions for bam neural networks with distributed leakage delays on time scales, J. Appl. Anal. Comput., 2017, 7(4), 1200-1232. [47] M. Yan, J. Qiu, X. Chen, X. Chen, C. Yang and A. Zhang, Almost periodic dynamics of the delayed complex-valued recurrent neural networks with discontinuous activation functions, Neural Comput. Appl., 2018, 30(11), 3339-3352. doi: 10.1007/s00521-017-2911-1 [48] M. Yan, J. Qiu, X. Chen, X. Chen, C. Yang, A. Zhang and F. Alsaadi, The global exponential stability of the delayed complex-valued neural networks with almost periodic coefficients and discontinuous activations, Neural Process. Lett., 2018, 48(1), 577-601. doi: 10.1007/s11063-017-9736-x [49] B. Zhou and Q. Song, Boundedness and complete stability of complex-valued neural networks with time delay, IEEE Trans. Neural Netw. Learn. Syst., 2013, 24(8), 1227-1238. doi: 10.1109/TNNLS.2013.2247626 [50] Z. Zhang, D. Hao and D. Zhou, Global asymptotic stability by complex-valued inequalities for complex-valued neural networks with delays on period time scales, Neurocomputing, 2107, 219, 494-501. -
-
-
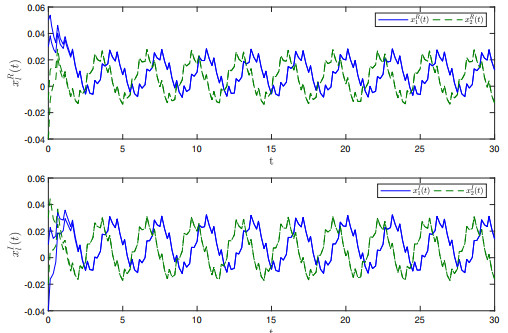
Figure 1.
$ \mathbb{T}=\mathbb{R} $ $ x_{1}(t) $ $ x_{2}(t) $ -
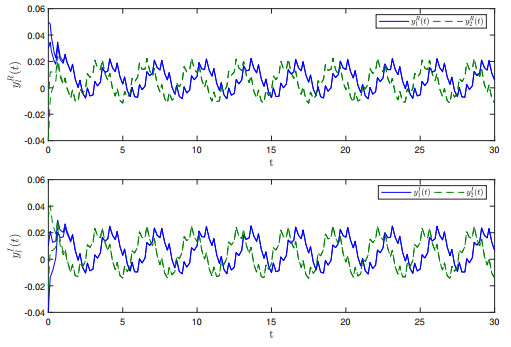
Figure 2.
$ \mathbb{T}=\mathbb{R} $ $ y_{1}(t) $ $ y_{2}(t) $ -
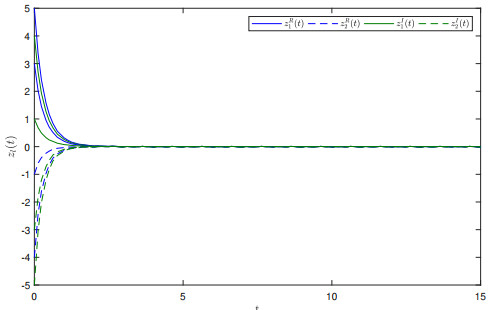
Figure 3.
$ \mathbb{T}=\mathbb{R} $ $ z(t)=y(t)-x(t) $ -
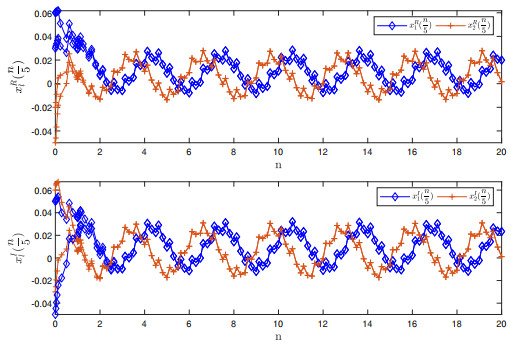
Figure 4.
$ \mathbb{T}=\frac{\mathbb{Z}}{5} $ $ x_{1}(\frac{n}{5}) $ $ x_{2}(\frac{n}{5}) $ -
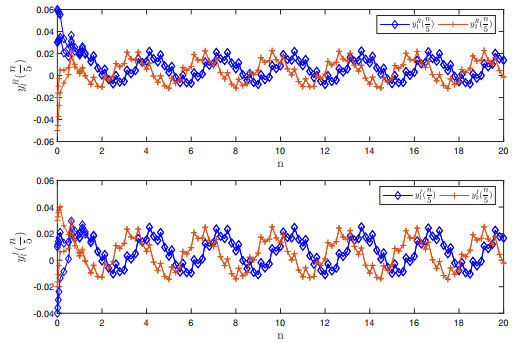
Figure 5.
$ \mathbb{T}=\frac{\mathbb{Z}}{5} $ $ y_{1}(\frac{n}{5}) $ $ y_{2}(\frac{n}{5}) $ -
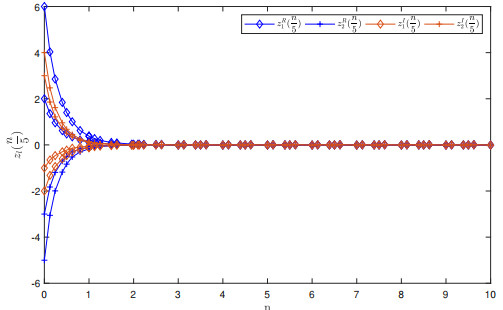
Figure 6.
$ \mathbb{T}=\frac{\mathbb{Z}}{5} $ $ z(\frac{n}{5})=y(\frac{n}{5})-x(\frac{n}{5}) $




 DownLoad:
DownLoad: