| Citation: | Na Chen, Deliang Zhu. THE GREEDY RANDOMIZED EXTENDED KACZMARZ ALGORITHM FOR NOISY LINEAR SYSTEMS[J]. Journal of Applied Analysis & Computation, 2023, 13(2): 913-927. doi: 10.11948/20220230 |
THE GREEDY RANDOMIZED EXTENDED KACZMARZ ALGORITHM FOR NOISY LINEAR SYSTEMS
-
Abstract
For solving the noisy linear systems, we propose a new greedy randomized extended Kaczmarz algorithm by introducing an effective greedy criterion for selecting the working rows and a randomized orthogonal projection for reducing the influence of the noisy term. We prove that the solution of the proposed greedy randomized extended Kaczmarz algorithm converges in expectation to the least squares solution of the given linear system. Theoretical analysis indicate that the convergence rate of the greedy randomized extended Kaczmarz algorithm is much faster than the randomized extended Kaczmarz method, and numerical results also show that the proposed greedy randomized extended Kaczmarz algorithm is superior to the randomized extended Kaczmarz method. Moreover, for noisy linear systems, the proposed algorithm is more effcient than the greedy randomized Kaczmarz algorithm.
-

-
References
[1] Z. Bai and W. Wu, On greedy randomized Kaczmarz method for solving large sparse linear systems, SIAM J. Sci. Comput., 2018, 40(1), 592-606. doi: 10.1137/17M1137747 [2] Z. Bai and W. Wu, On convergence rate of the randomized Kaczmarz method, Linear Algebra Appl., 2018, 553, 252-269. doi: 10.1016/j.laa.2018.05.009 [3] Z. Bai and W. Wu, On relaxed greedy randomized Kaczmarz methods for solving large sparse linear systems, Appl. Math. Lett., 2018, 83, 21-26. doi: 10.1016/j.aml.2018.03.008 [4] S. Kaczmarz, Angenäherte Auflösung von systemen linearer Gleichungen, Bull. Int. Acad. Pol. Sci. Lett. A, 1937, 35, 355-357. [5] D. A. Lorenz, S. Wenger, F. Schöofer and M. Magnor, A sparse Kaczmarz solver and a linearized Bregman method for online compressed sensing, IEEE International Conference on Image Processing (ICIP), Paris, France, 2014, 1347-1351. [6] J. Lin and D. Zhou, Learning theory of randomized Kaczmarz method, J. Machine Learning Res., 2015, 16(103), 3341-3365. [7] Y. Lei and D. Zhou, Learning theory of randomized sparse Kaczmarz method, SIAM J. Imaging Sci., 2018, 11(1), 547-574. doi: 10.1137/17M1136225 [8] A. Ma, D. Needell and A. Ramdas, Convergence properties of the randomized extended Gauss-Seidel and Kaczmarz methods, SIAM J. Matrix Anal. Appl., 2015, 36(4), 1590-1604. doi: 10.1137/15M1014425 [9] D. Needell, N. Srebro and R. Ward, Stochastic gradient descent, weighted sampling, and the randomized Kaczmarz algorithm, Math. Program., Ser. A, 2016, 155(1), 549-573. [10] D. Needell, Randomized Kaczmarz solver for noisy linear systems, BIT Numerical Mathematics, 2010, 50(2), 395-403. doi: 10.1007/s10543-010-0265-5 [11] C. Popa and R. Zdunek, Kaczmarz extended algorithm for tomographic image reconstruction from limited data, Math. Comput. Simulation, 2004, 65(6), 579-598. doi: 10.1016/j.matcom.2004.01.021 [12] E. Rebrova and D. Needell, On block Gaussian sketching for the Kaczmarz method, Numer. Algorithms, 2021, 86(1), 443-473. [13] F. Schöofer and D. A. Lorenz, Linear convergence of the randomized sparse Kaczmarz method, Math. Program., Ser. A, 2019, 173(1-2), 509-536. [14] T. Strohmer and R. Vershynin, A randomized Kaczmarz algorithm with exponential convergence, J. Fourier Anal. Appl., 2009, 15(2), 262-278. [15] O. Wang, W. Li, W. Bao and X. Gao, Nonlinear Kaczmarz algorithms and their convergence, J. Comput. Appl. Math., 2022, 399, 223720. [16] A. Zouzias and N. M. Freris, Randomized extended Kaczmarz for solving least squares, SIAM J. Matrix Anal. Appl., 2013, 34(2), 773-793. [17] J. Zhang, A new greedy Kaczmarz algorithm for the solution of very large linear systems, Appl. Math. Lett., 2019, 91, 207-212. -
-
-
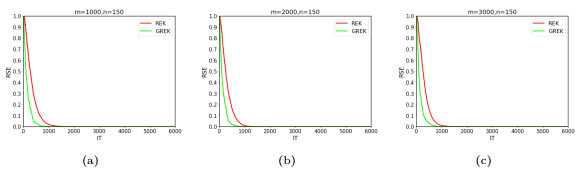
Figure 1.
RSE versus IT for GREK and REK with
$ m=1000, 2000, 3000 $ $ n=150 $ -
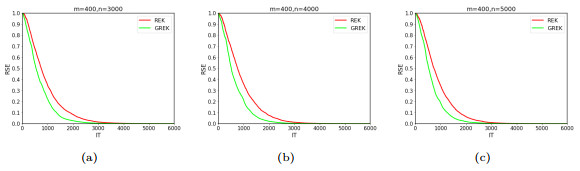
Figure 2.
RSE versus IT for GREK and REK with
$ m=400 $ $ n=3000, 4000, 5000 $ -
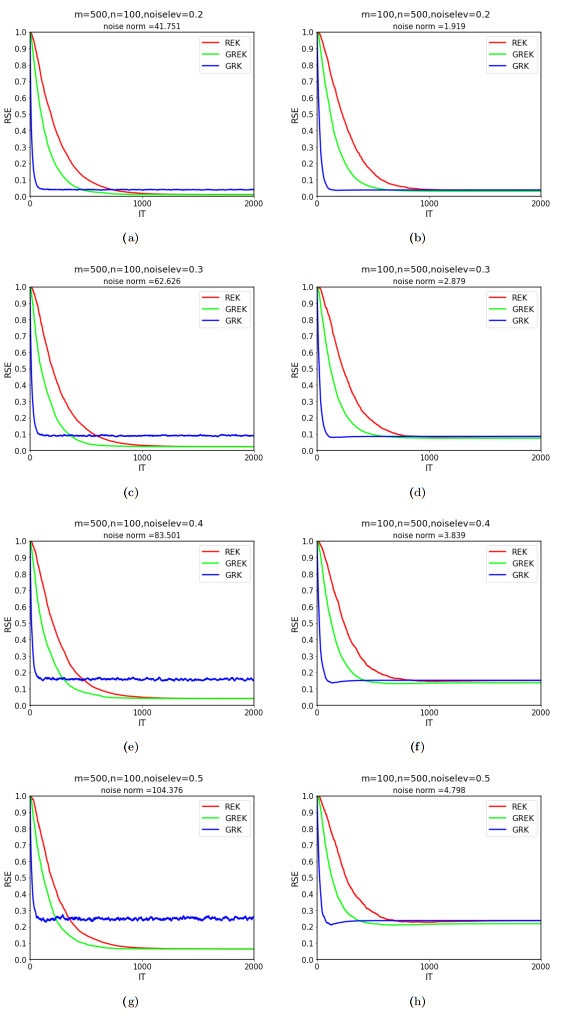
Figure 3.
RSE versus IT for GREK, GRK and REK with noisy linear systems with noisy level 0.2 (Row 1), 0.3 (Row 2), 0.4 (Row 3) and 0.5 (Row 4). Left: The results for overdetermined systems. Right: The results for underdetermined systems.




 DownLoad:
DownLoad: