| Citation: | Bayram Bala, Manaf Dzh. Manafov, Abdullah Kablan. SOLUTION AND CONSTRUCTION OF INVERSE PROBLEM FOR STURM-LIOUVILLE EQUATIONS WITH FINITELY MANY POINT δ-INTERACTIONS[J]. Journal of Applied Analysis & Computation, 2023, 13(1): 458-469. doi: 10.11948/20220287 |
SOLUTION AND CONSTRUCTION OF INVERSE PROBLEM FOR STURM-LIOUVILLE EQUATIONS WITH FINITELY MANY POINT δ-INTERACTIONS
-
Abstract
The goal of this paper is to reconstruct a one kind of Sturm-Liouville problem from its spectral properties. We considered the inverse spectral problems for a Sturm-Liouville equations with finitely many delta-interactions. We obtain the effective method and its steps to find the solution of the inverse problems and then we will give an example to illustrate this method.
-
Keywords:
- Inverse problems /
- Sturm-Liouville equation /
- Point δ-interactions
-

-
References
[1] S. Albeverio, F. Gesztesy, R. Hoegh-Krohn and H. Holden (with an appendix by P. Exner), Solvable Models in Quantum Mechanics (second edition), AMS Chelsea Publ., 2005. [2] R. Bellman and K. Cooke, Differantial-Difference Equations, Academic Press, New York, 1963. [3] E. A. Coddington and N. Levinson, Theory of Ordinary Differantial Equations, McGraw-Hill, New York, 1955. [4] J. B. Conway, Functions of One Complex Variable (2nd edition), Springer, New York, 1995. [5] G. Freiling and V. A. Yurko, Inverse Sturm-Liouville Problems and Their Applications, Nova Science Publ., Inc: Huntington, New York, 2001. [6] N. J. Guliyev, On two-spectra inverse problems, Proc. of the American Math. Soc., 2020, 148(10), 4491–4502. doi: 10.1090/proc/15155 [7] Y. Guo and G. Wei, On the reconstruction of the Sturm-Liouville problems with spectral parameter in the discontinuity conditions, Results Math., 2014, 65, 385–398. doi: 10.1007/s00025-013-0352-4 [8] O. H. Hald, Discontinuous inverse eigenvalue problems, Comm. on Pure and Appl. Math., 1986, 37(5), 53–72. [9] A. Kablan and M. D. Manafov, Sturm-Liouville problems with finitely many point $\delta $-interactions and eigen-parameter in boundary conditions, Miskolc Math. Notes, 2016, 17(2), 911–923. $\delta $-interactions and eigen-parameter in boundary conditions" target="_blank">Google Scholar
[10] R. Kronig and W. G. Penney, Quantum mechanics of electrons in crystal lattices, Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1931, 130(814), 443–517. [11] B. M. Levitan and I. S. Sargsyan, Introduction to Spectral Theory, AMS Trans. of Math. Monogr., Providence, 1975, 39. [12] B. M. Levitan, Inverse Sturm-Liouville Problems, VSP, Zeist, 1987. [13] Y. Liu, G. Shi and J. Yan, An inverse problem for non-selfadjoint Sturm-Liouville operator with discontinuity conditions inside a finite interval, Inverse problems in Sci. and Engineering, 2019, 27(3), 407–421. doi: 10.1080/17415977.2018.1470624 [14] M. D. Manafov, Description of the domain of an ordinary differential operator with generalized potentials, Differ. Uravneniya, 1996, 32(5), 706–707, Eng. transl. : Differential Equations, 1996, 32(5), 716–718. [15] M. D. Manafov, Inverse spectral problems for energy-dependent Sturm-Liouville equations with finitely many point $\delta $-interactions, Elect. J. Differ. Equations, 2016, 2016(11), 1–12. [16] M. D. Manafov, Inverse spectral problems for energy-dependent Sturm-Liouville equations with $\delta $-interaction, Filomat, 2016, 30(11), 2935–2946. doi: 10.2298/FIL1611935M CrossRef $\delta $-interaction" target="_blank">Google Scholar
[17] M. D. Manafov, Inverse spectral and inverse nodal problems for Sturm-Liouville equations with point $\delta $ and $\delta^{\prime }$-interactions, Proceedings of the Ins. Math. and Mech. NAS of Azerbaijan, 2019, 45(2), 286–294. $\delta $ and
$\delta^{\prime }$ [18] V. A. Marchenko, Sturm-Liouville Operators and Their Applications, Operator Theory: Advanced and Application, Birkhauser, Basel, 1986. [19] X. Xu and C. Yang, Inverse spectral problems for the Sturm-Liouville operator with discontinuity, J. Diff. Equations, 2017, 262, 3093–3106. doi: 10.1016/j.jde.2016.11.024 [20] X. Xu, Inverse spectral problems fort he generalized Robin-Regge problem with complex coefficients, J. of Geometry and Physics, 2021, 159(103936), 1–10. [21] X. Xu, L. Ma and C. Yang, On the stability of the inverse transmission eigenvalue problem from the data of McLaughlin and Polyakov, J. of Diff. Equations, 2022, 316(2022), 222–248. [22] V. A. Yurko, Boundary value problems with discontinuity conditions in an interior point of the interval, Differ. Uravneniya, 2000, 36(8), 1139–1140, Eng. transl.: Differential Equations, 2000, 36(8), 1266–1269. [23] V. A. Yurko, On the inverse problem for differential operators on a finite interval with complex weights, Mat. Zametki, 2019, 105(2), 313–320, Eng. transl. : Math. Notes, 2019, 105(2), 301–306. [24] R. Zhang, N. P. Bondarenko and C. Yang, Solvability of an inverse problem for discontinuous Sturm- Liouville operators, Math. Methods in the Appl. Sci., 2021, 44(1), 124–139. -
-
-
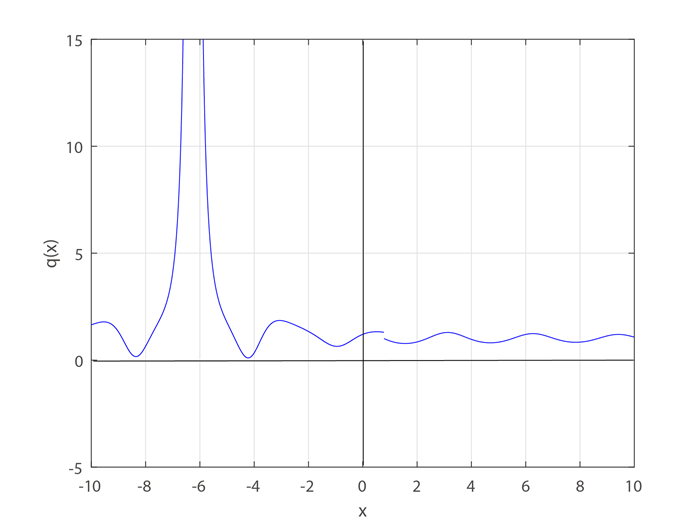
Figure 1.
The graph of
$q(x)$ $x=\pi/4$




 DownLoad:
DownLoad: