| Citation: | Lili Jia, Xiaojuan Zhao, Changyou Wang, Qiyu Wang. DYNAMIC BEHAVIOR OF A SEVEN-ORDER FUZZY DIFFERENCE EQUATION[J]. Journal of Applied Analysis & Computation, 2023, 13(1): 486-501. doi: 10.11948/20220340 |
DYNAMIC BEHAVIOR OF A SEVEN-ORDER FUZZY DIFFERENCE EQUATION
-
Abstract
In this paper, we explore the qualitative features of a seven-order fuzzy difference equation
$x_{n+1}=\frac{A x_{n-1}}{B+C x_{n-2}^{p} x_{n-4}^{q} x_{n-6}^{r}}, n=0, 1, 2, \cdots, $
here the parameters $A, B, C$ $\in$ $R$$_f^+$, $p, q, r$ $\in$ $R$$^+$ and the initial values $x$$_{-6}$, $\cdots$, $x$$_{-1}$, $x$$_{0}$$\in$ $R$$_f^+$. Utilizing the fuzzy sets theory, linearization method, mathematical induction and inequality technique, we obtain some sufficient condition on the qualitative features including the boundedness of the positive solution of the equation and the stability and instability of the equilibrium point of the equation. Moreover, two simulation examples are presented to verify the effectiveness of our proposed results.
-
Keywords:
- Fuzzy difference equation /
- equilibrium point /
- boundedness /
- stability /
- unstability
-

-
References
[1] R. Abo-Zeid, Global behavior of a higher order difference equation, Mathematica Slovaca, 2014, 64(4), 931–940. [2] R. Abo-Zeid, On the oscillation of a third order rational difference equation, Journal of the Egyptian Mathematical Society, 2015, 23(1), 62–66. doi: 10.1016/j.joems.2014.03.001 [3] R. Abo-Zeid, On the solutions of a higher order difference equation, Georgian Mathematical Journal, 2020, 27(2), 165–175. doi: 10.1515/gmj-2018-0008 [4] A. M. Ahmed and H. M. Rezk, On the dynamics of the recursive sequence $x_{n+1}=b x_{n-1} /\left(A+B x_{n}^{p} x_{n-2}^{q}\right)$, Journal of Pure and Applied Mathematics: Advances and Applications, 2009, 1(2), 215–223. $x_{n+1}=b x_{n-1} /\left(A+B x_{n}^{p} x_{n-2}^{q}\right)$" target="_blank">Google Scholar
[5] F. Belhannache, Asymptotic stability of a higher order rational difference equation, Electronic Journal of Mathematical Analysis and Applications, 2019, 7(2), 1–8. [6] K. A. Chrysafifis, B. K. Papadopoulos and G. Papaschinopoulos, On the fuzzy difference equations of finance, Fuzzy Sets and Systems, 2008, 159(24), 3259–3270. doi: 10.1016/j.fss.2008.06.007 [7] I. Dekkar, N. Touafek and Q. Din, On the global dynamics of a rational difference equation with periodic coefficients, Journal of Applied Mathematics and Computing, 2019, 60(1–2), 567–588. [8] D. S. Dilip, A. Kılıçman and S. C. Babu, Asymptotic and boundedness behaviour of a rational difference equation, Journal of Difference Equations and Applications, 2019, 25(3), 305–312. doi: 10.1080/10236198.2019.1568424 [9] M. E. Erdogan and K. Uslu, On the dynamics of the difference equation $ x_{n+1}=\alpha x_{n-3} /\left(\beta+\gamma x_{n} x_{n-1} x_{n-2} x_{n-3}\right) $, International Journal of Engineering and Applied Sciences, 2016, 3(7), 80–82. [10] Y. Halim and J. F. T. Rabago, On the solutions of a second-order difference equation in terms of generalized Padovan sequences, Mathematica Slovaca, 2018, 68(3), 625–638. doi: 10.1515/ms-2017-0130 [11] L. Jia, C. Wang, X. Zhao and W. Wei, Dynamic behavior of a fractional-type fuzzy difference system, symmetry, 2022, 14(7), Article ID: 1337. doi: 10.3390/sym14071337 [12] S. Kalabu$\breve{\text{s}}$ić, M. R. S. Kulenović and C. B. Overdeep, Dynamics of the recursive sequence $x_{n+1}=\left(\beta x_{n-l}+\delta x_{n-k}\right) /\left(B x_{n-l}+D x_{n-k}\right)$, Journal of Difference Equations and Applications, 2004, 10(10), 915–928. doi: 10.1080/10236190410001731425 CrossRef $x_{n+1}=\left(\beta x_{n-l}+\delta x_{n-k}\right) /\left(B x_{n-l}+D x_{n-k}\right)$" target="_blank">Google Scholar
[13] M. A. Kerker, E. Hadidi and A. Salmi, Qualitative behavior of a higher-order nonautonomous rational difference equation, Journal of Applied Mathematics and Computing, 2020, 64(1), 399–409. [14] A. Khastan, New solutions for first order linear fuzzy difference equations, Journal of Computational and Applied Mathematics, 2017, 312, 156–166. doi: 10.1016/j.cam.2016.03.004 [15] A. Khastan and Z. Alijani, On the new solutions to the fuzzy difference equation $x_{n+1}=A+B / x_{n}$, Fuzzy Sets and Systems, 2019, 358, 64–83. doi: 10.1016/j.fss.2018.03.014 CrossRef $x_{n+1}=A+B / x_{n}$" target="_blank">Google Scholar
[16] Z. Li, Y. Jiang, C. Hu, et al., Difference equation based empirical mode decomposition with application to separation enhancement of multi-fault vibration signals, Journal of Difference Equations and Applications, 2017, 23(1–2), 457–467. [17] J. Liu, P. Wang, Y. Huang, et al., Power load combination forecasting based on triangular fuzzy discrete difference equation forecasting model and PSO-SVR, Journal of Intelligent & Fuzzy Systems, 2019, 36(6), 5889–5898. [18] G. Papaschinopoulos, C. J. Schinas and G. Ellina, On the dynamics of the solutions of a biological model, Journal of Difference Equations and Applications, 2014, 20(5–6), 694–705. [19] M. Saleh, N. Alkoumi and A. Farhat, On the dynamics of a rational difference equation $x_{n+1}=\left(\alpha+\beta x_{n}+\gamma x_{n k-k}\right) /\left(B x_{n}+C x_{n-k}\right)$, Chaos, Solitons & Fractals, 2017, 96, 76–84. [20] M. Saleh and S. Hirzallah, Dynamics and bifurcation of a second order rational difference equation with quadratic terms, Journal of Applied Nonlinear Dynamics, 2021, 10(3), 561–576. [21] H. Sedaghat, Nonlinear Difference Equations: Theory with Applications to Social Science Models, Kluwer Academic Publishers, Dordrecht, 2003. [22] G. Stefanidou and G. Papaschinopoulos, The periodic nature of the positive solutions of a nonlinear fuzzy max-difference equation, Information Sciences, 2006, 176(24), 3694–3710. doi: 10.1016/j.ins.2006.02.006 [23] L. Stefanini, A generalization of Hukuhara difference and division for interval and fuzzy arithmetic, Fuzzy sets and systems, 2010, 161(11), 1564–1584. doi: 10.1016/j.fss.2009.06.009 [24] S. Stević, On the difference equation $x_{n}=x_{n-k} /\left(b+c x_{n-1} \cdots x_{n-k}\right)$, Applied Mathematics and Computation, 2012, 218(11), 6291–6296. doi: 10.1016/j.amc.2011.11.107 CrossRef $x_{n}=x_{n-k} /\left(b+c x_{n-1} \cdots x_{n-k}\right)$" target="_blank">Google Scholar
[25] G. Su, T. Sun and B. Qin, Global Behavior of a higher order fuzzy difference equation, Mathematics, 2019, 7(10), Article ID: 938. doi: 10.3390/math7100938 [26] C. Wang and J. Li, Periodic Solution for a Max-Type Fuzzy Difference Equation, Journal of Mathematics, 2020, 2020, Article ID: 3094391. [27] C. Wang, J. Li and L. Jia, Dynamics of a high-order nonlinear fuzzy difference equation, Journal of Applied Analysis and Computation, 2021, 11(1), 404–421. doi: 10.11948/20200050 [28] C. Wang, X. Zhao, L. Jia and T. Jiang, Existence and uniqueness of solution for a class of seven-order exponential fuzzy difference equations, Journal of Applied Mathematics and Computation, 2022, 6(1), 66–70. doi: 10.26855/jamc.2022.03.009 [29] R. Willox, B. Grammaticos, A. S. Carstea and A. Ramani, Epidemic dynamics: discrete-time and cellular automaton models, Physica A: Statistical Mechanics and its Applications, 2003, 328(1–2), 13–22. [30] Q. Yang, J. Tian and W. Si, An improved particle swarm optimization based on difference equation analysis, Journal of Difference Equations and Applications, 2017, 23(1–2), 135–152. [31] Q. Zhang, F. Lin and X. Zhong, On discrete time Beverton-Holt population model with fuzzy environment, Mathematical Biosciences and Engineering, 2019, 16(3), 1471–1488. doi: 10.3934/mbe.2019071 [32] Q. Zhang, O. Miao, F. Lin and Z. Zhang, On discrete-time laser model with fuzzy environmen, AIMS Mathematics, 2021, 6(4), 3105–3120. doi: 10.3934/math.2021188 [33] Q. Zhang, W. Zhang, F. Lin, et al., On dynamic behavior of second-order exponential-type fuzzy difference equation, Fuzzy Sets and Systems, 2021, 419, 169–187. doi: 10.1016/j.fss.2020.07.021 -
-
-
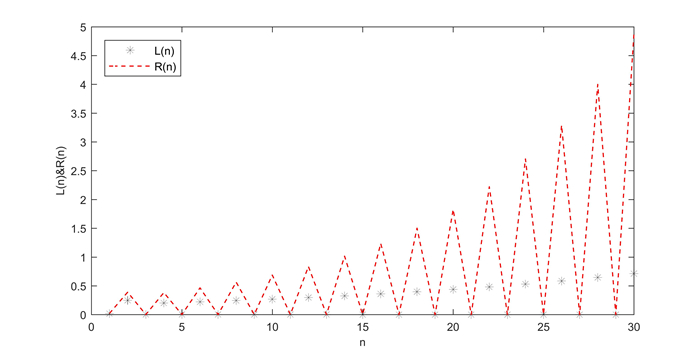
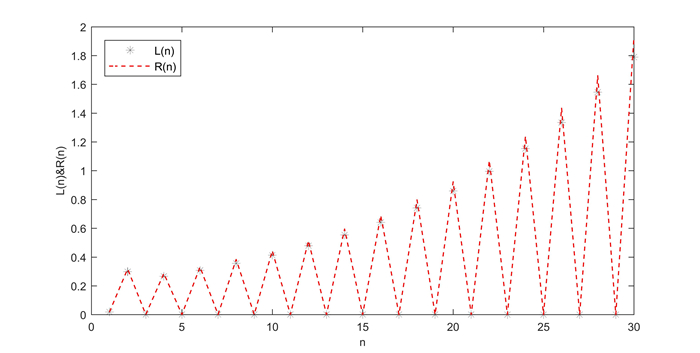
Figure 1.
The dynamics of system (3.4).
-
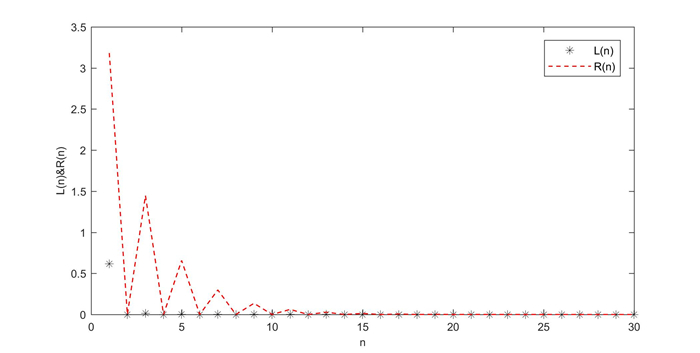
Figure 2.
The solution of system (3.4) at
$ \alpha =0 $ -
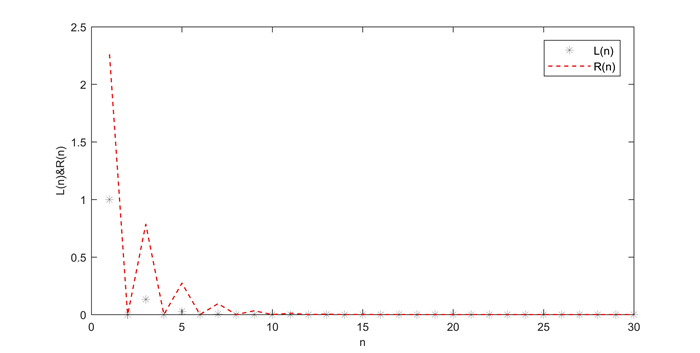
Figure 3.
The solution of system (3.4) at
$ \alpha =0.5 $ -
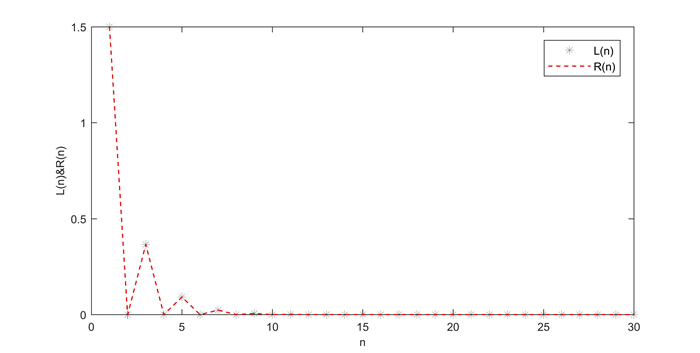
Figure 4.
The solution of system (3.4) at
$ \alpha =1 $ -
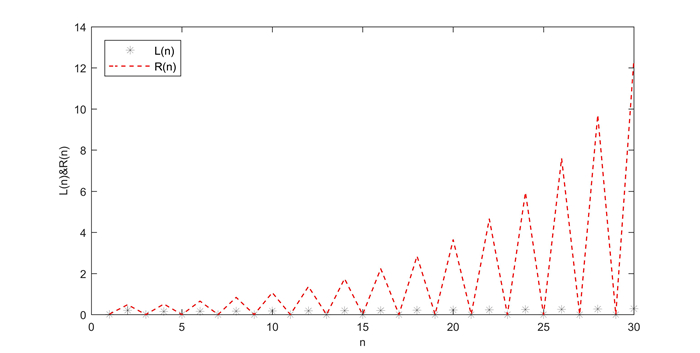
Figure 5.
The solution of system (3.5) at
$ \alpha =0 $ -
Figure 6.
The solution of system (3.5) at
$ \alpha =0.5 $ -
Figure 7.
The solution of system (3.5) at
$ \alpha =1 $




 DownLoad:
DownLoad: