| Citation: | Yanfei Dai, Minzhi Wei. EXISTENCE AND UNIQUENESS OF PERIODIC WAVES FOR A PERTURBED SEXTIC GENERALIZED BBM EQUATION[J]. Journal of Applied Analysis & Computation, 2023, 13(1): 502-525. doi: 10.11948/20220442 |
EXISTENCE AND UNIQUENESS OF PERIODIC WAVES FOR A PERTURBED SEXTIC GENERALIZED BBM EQUATION
-
Abstract
This paper is devoted to the existence and uniqueness of periodic waves for a perturbed sextic generalized BBM equation with weak backward diffusion and dissipation effects. By applying geometric singular perturbation theory and analyzing the perturbations of a Hamiltonian system with a hyper-elliptic Hamiltonian of degree seven, we prove the existence and uniqueness of periodic wave solutions with each wave speed in an open interval. It is also proved that the periodic wave solution persists for any energy parameter $h$ in an open interval and sufficiently small perturbation parameter. Furthermore, we prove that the wave speed $c_0(h)$ is strictly monotonically increasing with respect to $h$ by analyzing Abelian integral having three generating elements. Moreover, the upper and lower bounds of the limiting wave speed are obtained.
-

-
References
[1] Y. An, M. Han, On the number of limit cycles near a homoclinic loop with a nilpotent singular point, J. Diff. Eqs., 2015, 258(9), 3194–3247. doi: 10.1016/j.jde.2015.01.006 [2] T. Benjamin, J. Bona, J. Mahony, Model equations for long waves in nonlinear dispersive systems, Phil. Trans. R. Soc. Lond. A, 1972, 272(1220), 47–78. doi: 10.1098/rsta.1972.0032 [3] C. Besse, B. Mésognon-Gireau, P. Noble, Artificial boundary conditions for the linearized Benjamin-Bona-Mahony equation, Numer. Math., 2018, 139(2), 281–314. doi: 10.1007/s00211-017-0943-1 [4] A. Biswas, 1-Soliton solution of Benjamin-Bona-Mahoney equation with dual-power law nonlinearity, Commun. Non. Sci Numer. Simul., 2010, 15(10), 2744–2746. doi: 10.1016/j.cnsns.2009.10.023 [5] R. Camassa and D. Holm, An integrable shallow wave equation with peaked solitons, Phys. Rev. Lett., 1993, 71(11), 1661–1664. doi: 10.1103/PhysRevLett.71.1661 [6] A. Chen, L. Guo, X. Deng, Existence of solitary waves and periodic waves for a perturbed generalized BBM equation, J. Diff. Equat., 2016, 261(10), 5324–5349. doi: 10.1016/j.jde.2016.08.003 [7] A. Chen, L. Guo and W. Huang, Existence of kink waves and periodic waves for a perturbed defocusing mKdV equation, Qual. Theory Dyn. Syst., 2018, 17(3), 495–517. doi: 10.1007/s12346-017-0249-9 [8] G. Collins, The calculation of multivariate polynomial resultants, J. Assoc. Comput. Mach., 1971, 18(4), 515–532. doi: 10.1145/321662.321666 [9] Y. Dai, M. Wei, M. Han, Periodic waves for a perturbed generalized BBM equation, preprint. [10] Y. Dai, Y. Zhao, B. Sang, Four limit cycles in a predator-prey system of Leslie type with generalized Holling type III functional response, Nonlinear Anal. Real World Appl., 2019, 50, 218-239. doi: 10.1016/j.nonrwa.2019.04.003 [11] G. Derks and S. van Gils, On the uniqueness of traveling waves in perturbed Korteveg-deVries equations, Japan J. Indust. Appl. Math., 1993, 10(3), 413–430. doi: 10.1007/BF03167282 [12] X. Fan and L. Tian, The existence of solitary waves of singularly perturbed mKdV-KS equation, Chaos Solitons Fractals, 2005, 26(4), 1111–1118. doi: 10.1016/j.chaos.2005.02.014 [13] N. Fenichel, Geometric singular perturbation theory for ordinary differential equations, J. Diff. Equat., 1979, 31(1), 53–98. doi: 10.1016/0022-0396(79)90152-9 [14] I. Gelfand, M. Kapranov, A. Zelevinsky, Discriminants, Resultants and Multidimensional Determinants, Birkhäser, Boston, 1994. [15] M. Grau, F. Mañsas, J. Villadelprat, A Chebyshev criterion for Abelian integrals, Trans. Am. Math. Soc., 2011, 363(1), 109–129. doi: 10.1090/S0002-9947-2010-05007-X [16] A. Green and P. Naghdi, A derivation of equations for wave propagation in water of variable depth, J. Fluid. Mech., 1976, 78(02), 237–246. doi: 10.1017/S0022112076002425 [17] L. Guo and Y. Zhao, Existence of periodic waves for a perturbed quintic BBM equation, Discrete Contin. Dyn. Syst. Ser. B, 2020, 40(8), 46894703. [18] M. Han, Bifurcation theory and periodical solution of dynamic system, Science Press, Beijing, 2002. [19] M. Han, Bifurcation theory of limit cycles, Science Press, Beijing, 2013. [20] M. Han, J. Yang, The maximum number of zeros of functions with parameters and application to differential equations, Journal of Nonlinear Modeling and Analysis, 2021, 3(1), 13–34. [21] M. Han, J. Yang, D. Xiao, Limit cycle bifurcations near a double homoclinic loop with a nilpotent saddle, Internat. J. Bifur. Chaos Appl. Sci. Engrg., 2012, 22(8), 1250189-1-33. doi: 10.1142/S0218127412501891 [22] M. Han, P. Yu, Normal forms, Melnikov functions and bifurcations of limit cycles, Springer, New York, 2012. [23] C. Jones, Geometric singular perturbation theory: Dynamic systems, Lecture Notes in Math., Springer, Berlin, 1995, 1609, 44–118. [24] S. Karlin, W. Studden, Tchebycheff systems: with applications in analysis and statistics, J. Amer. Statis. Assoc., 1967, 62(319), 1093. [25] D. Korteweg and G. de Vries, On the change of form of the long waves advancing in a rectangular canal, and on a new type of stationary waves, Philos. Mag., 1895, 39(240), 422–443. doi: 10.1080/14786449508620739 [26] F. Li, H. Li, Y. Liu, New double bifurcation of nilpotent focus, Int. J. Bifurcation Chaos, 2021, 31(4), 2150053. doi: 10.1142/S021812742150053X [27] Y. Liu, F. Li, Double bifurcation of nilpotent focus, Int. J. Bifurcation Chaos, 2015, 25(03), 1550036. doi: 10.1142/S0218127415500364 [28] X. Lu, L. Lu, A. Chen, New peakons and periodic peakons of the modified Camassa-Holm equation, Journal of Nonlinear Modeling and Analysis, 2020, 2(3), 345–353. [29] F. Mañosas, J. Villadelprat, Bounding the number of zeros of certain Abelian integrals, J. Diff. Equat., 2011, 251(6), 1656–1669. doi: 10.1016/j.jde.2011.05.026 [30] S. Micu, On the controllability of the linearized Benjamin-Bona-Mahony equation, SIAM J. Control. Optim., 2001, 39(6), 1677–1696. doi: 10.1137/S0363012999362499 [31] D. Novaes and J. Torregrosa, On extended chebyshev systems with positive accuracy, J. Math. Anal. Appl., 2017, 448(1), 171–186. doi: 10.1016/j.jmaa.2016.10.076 [32] T. Ogawa, Traveling wave solutions to a perturbed Korteweg-de Vries equation, Hiroshima Math. J., 1994, 24(2), 401–422. [33] K. Omrani, The convergence of fully discrete Galerkin approximations for the Benjamin-Bona-Mahony (BBM) equation, Appl. Math. Comput., 2006, 180(2), 614–621. [34] K. Singh, R. Gupta, S. Kumar, Benjamin-Bona-Mahony (BBM) equation with variable coefficients: similarity reductions and Painlevé analysis, Appl. Math. Comput., 2011, 217(16), 7021–7027. [35] X. Sun, P. Yu, Periodic travelling waves in a generalized BBM equation with weak backward diffusion and dissipation terms, Discrete Contin. Dyn. Syst. Ser. B, 2019, 24(2), 965–987. [36] J. Wang, M. Yuen, L. Zhang, Persistence of solitary wave solutions to a singularly perturbed generalized mKdV equation, Appl. Math. Lett., 2022, 124, 107668. doi: 10.1016/j.aml.2021.107668 [37] J. Wang, L. Zhang, E. Shchepakina, et al., Solitary waves of singularly perturbed generalized KdV equation with high order nonlinearity, Discrete Contin. Dyn. Syst. Ser. S, 2022, doi: 10.3934/dcdss.2022124. [38] A. Wazwaz, Exact solution with compact and noncompact structures for the one-dimensional generalized Benjamin-Bona-Mahony equation, Commun. Non. Sci. Numer. Simulat., 2005, 10(8), 855–867. doi: 10.1016/j.cnsns.2004.06.002 [39] W. Yan, Z. Liu, Y. Liang, Existence of solitary waves and periodic waves to a perturbed generalized KdV equation, Math. Model. Anal., 2014, 19(4), 537–555. doi: 10.3846/13926292.2014.960016 [40] P. Yu, F. Li, Bifurcation of limit cycles in a cubic-order planar system around a nilpotent critical point, J. Math. Anal. Appl., 2017, 453(2), 645–667. doi: 10.1016/j.jmaa.2017.04.019 [41] H. Zang, M. Han, D. Xiao, On Melnikov functions of a homoclinic loop through a nilpotent saddle for planar near-Hamiltonian systems, J. Differential Equations, 2008, 245(4), 1086–1111. doi: 10.1016/j.jde.2008.04.018 [42] X. Zhang, Homoclinic, heteroclinic and periodic orbits of singularly perturbed systems, Sci. China. Math., 2019, 62(9), 1687–1704. doi: 10.1007/s11425-017-9223-6 [43] L. Zhang, M. Han, M. Zhang, et al. A new type of solitary wave solution of the mKdV equation under singular perturbations, Int. J. Bifurcation Chaos, 2020, 30(11), 2050162. doi: 10.1142/S021812742050162X [44] L. Zhang, Y. Wang, C. Khalique, et al., Peakon and cuspon solutions of a generalized Camassa-Holm-Novikov equation, J. Appl. Anal. Comput., 2018, 8(6), 1938–1958. [45] L. Zhang, Y. Wang, C. Khalique, et al., New type of solitary wave solution with coexisting crest and trough for a perturbed wave equation, Nonlinear Dyn., 2021, 106(4), 3479–3493. doi: 10.1007/s11071-021-06975-2 [46] X. Zhao, W. Xu, S. Li, et al., Bifurcations of traveling wave solutions for a class of the generalized Benjamin-Bona-Mahony equation, Appl. Math. Comput., 2006, 175(2), 1760–1774. [47] X. Zhao, H. Jia, H. Zhou, et al., Bifurcations of travelling wave solutions in a non-linear dispersive equation, Chaos Solitons Fractals, 2008, 37(2), 525–531. doi: 10.1016/j.chaos.2006.09.028 [48] K. Zhu, Y. Wu, Z. Yu, et al., New solitary wave solutions in a perturbed generalized BBM equation, Nonlinear Dyn., 2019, 97(4), 2413–2423. doi: 10.1007/s11071-019-05137-9 [49] K. Zhuang, Z. Du, X. Lin, Solitary waves solutions of singularly perturbed higher-order KdV equation via geometric singular perturbation method, Nonlinear Dyn., 2015, 80(1–2), 629–635. -
-
-
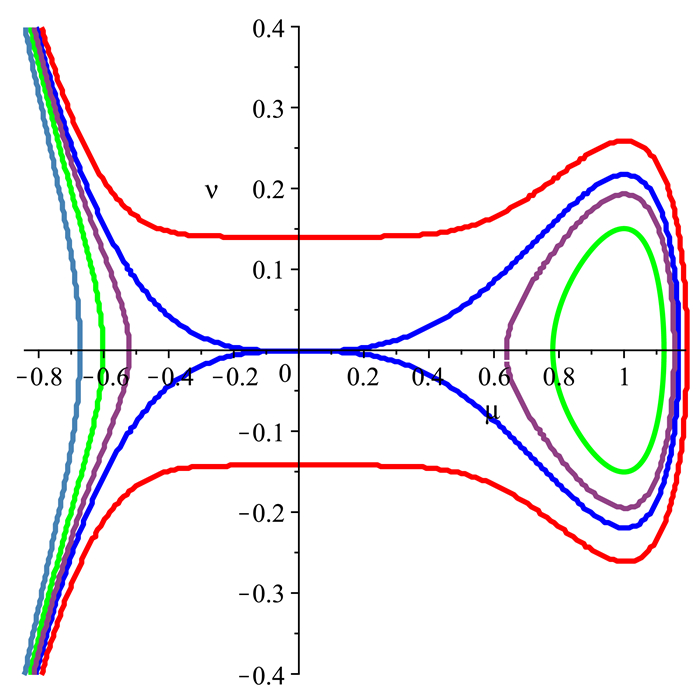
Figure 1.
The phase portrait of system (2.5).




 DownLoad:
DownLoad: