| Citation: | Satpal Singh, Devendra Kumar, Higinio Ramos. AN EFFICIENT PARAMETER UNIFORM SPLINE-BASED TECHNIQUE FOR SINGULARLY PERTURBED WEAKLY COUPLED REACTION-DIFFUSION SYSTEMS[J]. Journal of Applied Analysis & Computation, 2023, 13(4): 2203-2228. doi: 10.11948/20220446 |
AN EFFICIENT PARAMETER UNIFORM SPLINE-BASED TECHNIQUE FOR SINGULARLY PERTURBED WEAKLY COUPLED REACTION-DIFFUSION SYSTEMS
-
Abstract
A parameter-uniform numerical scheme for a system of weakly coupled singularly perturbed reaction-diffusion equations of arbitrary size with appropriate boundary conditions is investigated. More precisely, quadratic $B$-spline basis functions with an exponentially graded mesh are used to solve a $\ell\times\ell$ system whose solution exhibits parabolic (or exponential) boundary layers at both endpoints of the domain. A suitable mesh-generating function is used to generate the exponentially graded mesh. The decomposition of the solution into regular and singular components is obtained to provide error estimates. A convergence analysis is addressed, which shows a uniform convergence of the second order. To validate the theoretical findings, two test problems are solved numerically.
-

-
References
[1] M. P. Alam, D. Kumar and A. Khan, Trigonometric quintic $B$-spline collocation method for singularly perturbed turning point boundary value problems, Int. J. Comput. Math., 2021, 98(5), 1029–1048. doi: 10.1080/00207160.2020.1802016 CrossRef $B$-spline collocation method for singularly perturbed turning point boundary value problems" target="_blank">Google Scholar
[2] N. S. Bakhvalov, Towards optimization of methods for solving boundary value problems in the presence of boundary layers, Zh. Vychisl. Mat. Mat. Fiz., 1969, 9(4), 841–859. [3] G. I. Barenblatt, I. P. Zheltov and I. N. Kochina, Basic concepts in the theory of seepage of homogeneous liquids in fissured rocks, J. Appl. Math. Mech., 1960, 24(5), 1286–1303. doi: 10.1016/0021-8928(60)90107-6 [4] C. De Boor and B. Swartz, Collocation at Gaussian points, SIAM J. Numer. Anal., 1973, 10(4), 582–606. doi: 10.1137/0710052 [5] C. Clavero, J. L. Gracia and F. J. Lisbona, High order schemes for reaction-diffusion singularly perturbed systems, Lect. Notes Comput. Sci. Eng., 2009, 69, 107–115. [6] C. Clavero, J. L. Gracia and F. J. Lisbona, An almost third order finite difference scheme for singularly perturbed reaction-diffusion systems, J. Comput. Appl. Math., 2010, 234(8), 2501–2515. doi: 10.1016/j.cam.2010.03.011 [7] P. Constantinou and C. Xenophontos, Finite element analysis of an exponentially graded mesh for singularly perturbed problems, Comput. Methods Appl. Math., 2015, 15(2), 135–143. doi: 10.1515/cmam-2015-0002 [8] S. C. Cowin, Bone poroelasiticity, J. Biomech., 1999, 32(3), 217–238. doi: 10.1016/S0021-9290(98)00161-4 [9] P. Das and S. Natesan, Optimal error estimate using mesh equidistribution technique for singularly perturbed system of reaction-diffusion boundary-value problems, Appl. Math. Comput., 2014, 249, 265–277. [10] P. Das and J. Vigo-Aguiar, Parameter uniform optimal order numerical approximation of a class of singularly perturbed system of reaction diffusion problems involving a small perturbation parameter, J. Comput. Appl. Math., 2019, 354, 533–544. doi: 10.1016/j.cam.2017.11.026 [11] E. P. Doolan, J. J. H. Miller and W. H. A. Schilders, Uniform Numerical Methods for Problems with Initial and Boundary Layers, Boole Press, Dublin, 1980. [12] P. A. Farrell, P. W. Hemker and G. I. Shishkin, Discrete approximations for singularly perturbed boundary value problems with parabolic layers, J. Comput. Math., 1996, 14(1), 71–97. [13] P. A. Farrell, A. F. Hegarty, J. J. H. Miller, E. O'Riordan and G. I. Shishkin, Robust Computational Techniques for Boundary Layers, Chapman & Hall/CRC, Boca Raton, FL, 2000. [14] W. J. Kammerer, G. W. Reddien and R. S. Varga, Quadratic interpolatory splines, Numer. Math., 1974, 22, 241–259. doi: 10.1007/BF01406966 [15] Y. Kan-On and M. Mimura, Singular perturbation approach to a 3-component reaction-diffusion system arising in population dynamics, SIAM J. Math. Anal., 1998, 29(6), 1519–1536. doi: 10.1137/S0036141097318328 [16] R. B. Kellogg, N. Madden and M. Stynes, A parameter-robust numerical method for a system of reaction-diffusion equations in two dimensions, Numer. Methods Partial Differential Equations, 2008, 24, 312–334. doi: 10.1002/num.20265 [17] R. B. Kellogg, T. Linß and M. Stynes, A finite difference method on layer-adapted meshes for an elliptic reaction-diffusion system in two dimensions, Math. Comp., 2008, 77(264), 2085–2096. doi: 10.1090/S0025-5718-08-02125-X [18] N. Kopteva, Maximum norm a posteriori error estimates for a 1D singularly perturbed semilinear reaction diffusion problem, IMA J. Numer. Anal., 2007, 27(3), 576–592. [19] D. Kumar, A parameter-uniform scheme for the parabolic singularly perturbed problem with a delay in time, Numer. Methods Partial Differential Equations, 2021, 37(1), 626–642. doi: 10.1002/num.22544 [20] D. Kumar and P. Kumari, Uniformly convergent scheme for two-parameter singularly perturbed problems with non-smooth data, Numer. Methods Partial Differential Equations, 2021, 37(1), 796–817. doi: 10.1002/num.22553 [21] O. A. Ladyzhenskaya and N. N., Ural'tseva, Linear and quasilinear elliptic equations, Leon Ehrenpreis Academic Press, New York, 1968. [22] R. Lin and M. Stynes, A balanced finite element method for a system of singularly perturbed reaction-diffusion two-point boundary value problems, Numer. Algorithms, 2015, 70, 691–707. doi: 10.1007/s11075-015-9969-6 [23] T. Linß, An upwind difference scheme on a novel Shishkin-type mesh for a linear convection-diffusion problem, J. Comput. Appl. Math., 1999, 110(1), 93–104. doi: 10.1016/S0377-0427(99)00198-3 [24] T. Linß, Analysis of a Galerkin finite element Shishkin mesh for a linear convection-diffusion method on a Bakhvalov-problem, IMA J. Numer. Anal., 2000, 20(4), 621–632. doi: 10.1093/imanum/20.4.621 [25] T. Linß and N. Madden, Accurate solution of a system of coupled singularly perturbed reaction-diffusion equations, Computing, 2004, 73, 121–133. [26] T. Linß and N. Madden, A finite element analysis of a coupled system of singularly perturbed reaction-diffusion equations, Appl. Math. Comput., 2004, 148(3), 869–880. [27] T. Linß, Layer-adapted meshes for one-dimensional reaction-convection-diffusion problems, J. Numer. Math., 2004, 12(3), 193–205. doi: 10.1515/1569395041931482 [28] T. Linß and N. Madden, Layer-adapted meshes for a linear system of coupled singularly perturbed reaction-diffusion problems, IMA J. Numer. Anal., 2009, 29(1), 109–125. [29] T. Linß, Analysis of a FEM for a coupled system of singularly perturbed reaction-diffusion equations, Numer. Algorithms, 2009, 50, 283–291. doi: 10.1007/s11075-008-9228-1 [30] T. Linß, G. Radojev and H. Zarin, Approximation of singularly perturbed reaction-diffusion problems by quadratic $C.1$-splines, Numer. Algorithms, 2012, 61, 35–55. doi: 10.1007/s11075-011-9529-7 [31] N. Madden, Numerical methods for wave-current interactions, Ph. D., National University of Ireland, Cork, 2000. [32] N. Madden and M. Stynes, A uniformly convergent numerical method for a coupled system of singularly perturbed linear reaction-diffusion problems, IMA J. Numer. Anal., 2003, 23(4), 627–644. doi: 10.1093/imanum/23.4.627 [33] M. J. Marsden, Quadratic spline interpolation, Bull. Amer. Math. Soc., 1974, 80(5), 903–906. doi: 10.1090/S0002-9904-1974-13566-4 [34] S. Matthews, Parameter robust methods for a system of coupled singularly perturbed ordinary differential reaction-diffusion equations, M. Sc., School of Mathematical Sciences, Dublin City University, 2000. [35] S. Matthews, J. J. H. Miller, E. O'Riordan and G. I. Shishkin, Parameter-robust numerical methods for a system of reaction-diffusion problems with boundary layers, in: J.J.H. Miller, G.I. Shishkin, L. Vulkov (Eds. ), Analytical and Numerical Methods for Convection-Dominated and Singularly Perturbed Problems, Nova Science Publishers, Inc., New York, USA, 2000, 219–224. [36] S. Matthews, E. O'Riordan and G. I. Shishkin, A numerical method for a system of singularly perturbed reaction-diffusion equations, J. Comput. Appl. Math., 2002, 145(1), 151–166. doi: 10.1016/S0377-0427(01)00541-6 [37] J. J. H. Miller, E. O'Riordan and G. I. Shishkin, On piecewise-uniform meshes for upwind and central-difference operators for solving singularly perturbed problems, IMA J. Numer. Anal., 1995, 15(1), 89–99. doi: 10.1093/imanum/15.1.89 [38] J. J. H. Miller, E. O'Riordan and G. I. Shishkin, Fitted Numerical Methods for Singular Perturbation Problems, World Scientific, Singapore, 1996. [39] D. S. Naidu and A. J. Calise, Singular perturbations and time scales in guidance and control of aerospace systems: a survey, J. Guid. Control Dyn., 2001, 24(6), 1057–1078. doi: 10.2514/2.4830 [40] S. Natesan and B. S. Deb, A Robust computational method for singularly perturbed coupled system of reaction-diffusion boundary-value problems, Appl. Math. Comput., 2007, 188(1), 353–364. [41] T. A. Nhan and R. Vulanović, The Bakhvalov mesh: a complete finite-difference analysis of two-dimensional singularly perturbed convection-diffusion problems, Numer. Algorithms, 2021, 87, 203–221. doi: 10.1007/s11075-020-00964-z [42] M. H. Protterand H. F. Weinberger, On the spectrum of general second-order operators, Bull. Amer. Math. Soc., 1966, 72, 251–255. doi: 10.1090/S0002-9904-1966-11485-4 [43] E. O'Riordan and M. Stynes, A uniformly accurate finite-element method for a singularly perturbed one-dimensional reaction-diffusion problem, Math. Comp., 1986, 47(176), 555–570. doi: 10.1090/S0025-5718-1986-0856702-7 [44] W. Rodi, Turbulence Models and Their Applications in Hydraulics (A. A. Balkema, ed. ), IAHR Monograph Series, Rotterdam, 3rd edition, 1993. [45] H. G. Roos, M. Stynes and L. Tobiska, Numerical Methods for Singularly Perturbed Differential Equations, Convection-Diffusion and Flow Problems, Springer-Verlag, New York, 1996. [46] W. Ruan and C. Pao, Asymptotic behavior and positive solutions of a chemical reaction diffusion system, J. Math. Anal. Appl., 1992, 169(1), 157–178. doi: 10.1016/0022-247X(92)90109-Q [47] G. I. Shishkin, Mesh approximation of singularly perturbed boundary-value problems for systems of elliptic and parabolic equations, Comput. Maths. Math. Phys., 1995, 4(35), 429–446. [48] M. Shivhare, P. C. Podila and D. Kumar, A uniformly convergent quadratic $B$-spline collocation method for singularly perturbed parabolic partial differential equations with two small parameters, J. Math. Chem., 2021, 59, 186–215. doi: 10.1007/s10910-020-01190-7 CrossRef $B$-spline collocation method for singularly perturbed parabolic partial differential equations with two small parameters" target="_blank">Google Scholar
[49] G. Singh and S. Natesan, A uniformly convergent numerical scheme for a coupled system of singularly perturbed reaction-diffusion equations, Numer. Funct. Anal. Opti., 2020, 41(10), 1172–1189. doi: 10.1080/01630563.2020.1740255 [50] S. Singh, D. Kumar and H. Ramos, A uniformly convergent quadratic $B$-spline based scheme for singularly perturbed degenerate parabolic problems, Math. Comput. Simulation, 2022, 195, 88–106. doi: 10.1016/j.matcom.2021.12.026 CrossRef $B$-spline based scheme for singularly perturbed degenerate parabolic problems" target="_blank">Google Scholar
[51] M. Stephens and N. Madden, A parameter-uniform Schwarz method for a coupled system of reaction-diffusion equations, J. Comput. Appl. Math., 2009, 230(2), 360–370. doi: 10.1016/j.cam.2008.12.009 [52] G. P. Thomas, Towards an improved turbulence model for wave-current interactions, in: Second Annual Report to EU MAST-Ⅲ Project "The Kinematics and Dynamics of Wave-Current Interactions", 1998. [53] T. Valanarasu and N. Ramanujam, An asymptotic initial value method for boundary value problems for a system of singularly perturbed second order ordinary differential equations, Appl., Math. Comput., 2004, 147(1), 227–240. [54] R. Vulanović, Non-equidistant generalizations of the Gushchin-Schennikov scheme, ZAAM-J. Appl. Math. Mech., 1987, 67(12), 625–632. doi: 10.1002/zamm.19870671212 [55] H. Zarin, Exponentially graded mesh for singularly perturbed problem with two small parameters, Appl. Numer. Math., 2017, 120, 233–242. doi: 10.1016/j.apnum.2017.06.003 -
-
-
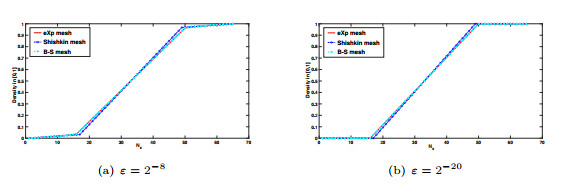
Figure 1.
Mesh comparison of eXp mesh, Shishkin mesh, B-S mesh for
$ N_{x}=64 $ -
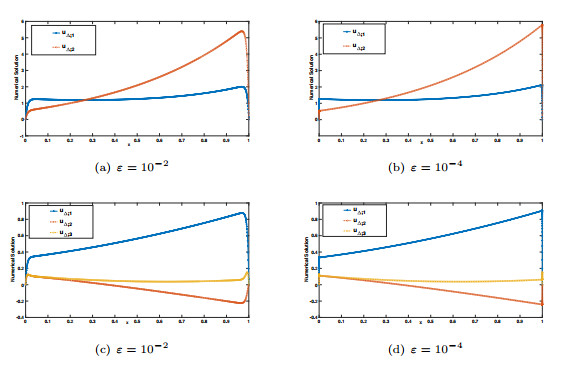
Figure 2.
Numerical solution plots of Example 5.1 (subfigures (a) and (b)), and Example 5.2 (subfigures (c) and (d))




 DownLoad:
DownLoad: