| Citation: | Mengxin Chen, Ranchao Wu, Qianqian Zheng. QUALITATIVE ANALYSIS OF A DIFFUSIVE COVID-19 MODEL WITH NON-MONOTONE INCIDENCE RATE[J]. Journal of Applied Analysis & Computation, 2023, 13(4): 2229-2249. doi: 10.11948/20220450 |
QUALITATIVE ANALYSIS OF A DIFFUSIVE COVID-19 MODEL WITH NON-MONOTONE INCIDENCE RATE
-
Abstract
The paper is concerned with a diffusive susceptible-asymptomatic-infected-recovered-type COVID-19 model with non-monotone incidence rate and homogeneous zero-flux boundary conditions. First the boundedness results of the diffusive COVID-19 model are established by the technique of the comparison principle of the parabolic equations. Then, we turn our attention to the corresponding elliptic equations. A priori estimates of the solutions are given, some properties of the positive steady states and nonexistence conditions of the positive steady states are presented by energy estimates. It is found that the diffusion rate of the proposed diffusive COVID-19 model could affect the existence of the nonconstant steady states. These qualitative results will give some theoretical insights into the diffusive COVID-19 model with non-monotone incidence rate.
-

-
References
[1] X. An and X. Song, A spatial SIS model in heterogeneous environments with vary advective rate, Math. Biosci. Eng., 2021, 18(5), 5449–5477. doi: 10.3934/mbe.2021276 [2] N. Ahmed, A. Elsonbaty, A. Raza, M. Rafiq and W. Adel, Numerical simulation and stability analysis of a novel reaction-diffusion COVID-19 model, Nonlinear Dyn., 2021, 106(2), 1293–1310. doi: 10.1007/s11071-021-06623-9 [3] T. A. Biala and A. Q. M. Khaliq, A fractional-order compartmental model for the spread of the COVID-19 pandemic, Commun. Nonlinear Sci. Numer. Simul., 2021, 98, 105764. doi: 10.1016/j.cnsns.2021.105764 [4] H. Cao, D. Yan and X. Xu, Hopf bifurcation for an SIR model with age structure, Math. Model. Nat. Phenom., 2021, 16(7), 1–17. [5] R. Cui, H. Li and R. Peng, Concentration behavior of endemic equilibrium for a reaction-diffusion-advection SIS epidemic model with mass action infection mechanism, Calc. Var. Partial Differ. Equ., 2021, 60(5), 184. doi: 10.1007/s00526-021-01992-w [6] T. Carvalho, R. Cristiano, D. S. Rodrigues and D. Tonon, Global Analysis of a piecewise smooth epidemiological model of COVID-19, Nonlinear Dyn., 2021, 105(4), 3763–3773. doi: 10.1007/s11071-021-06801-9 [7] M. Chen and R. Wu, Patterns in the predator-prey system with network connection and harvesting policy, Math. Meth. Appl. Sci., 2023, 46, 2433–2454. doi: 10.1002/mma.8653 [8] M. Chen, R. Wu and X. Wang, Non-constant steady states and Hopf bifurcation of a species interaction model, Commun. Nonlinear Sci. Numer. Simul., 2023, 116, 106846. doi: 10.1016/j.cnsns.2022.106846 [9] Y. Ding, Y. Fu and Y. Kang, Stochastic analysis of COVID-19 by a SEIR model with Levy noise, Chaos, 2021, 31(4), 043132. doi: 10.1063/5.0021108 [10] Q. Liu, D. Jiang, N. Shi, T. Hayat and A. Alsaedi, Stationarity and periodicity of positive solutions to stochastic SEIR epidemic models with distributed delay, Discret. Contin. Dyn. Syst. B, 2017, 22(6), 2479–2500. [11] C. Liu and R. Cui, Qualitative analysis on an SIRS reaction-diffusion epidemic model with saturation infection mechanism, Nonlinear Anal. : RWA, 2021, 62, 103364. doi: 10.1016/j.nonrwa.2021.103364 [12] Y. Lou and W. Ni, Diffusion, self-diffusion and cross-diffusion, J. Differ. Equations, 1996, 131(1), 79–131. doi: 10.1006/jdeq.1996.0157 [13] C. Lin, W. Ni and I. Takagi, Large amplitude stationary solutions to a chemotaxis system, J. Differ. Equations, 1988, 72(1), 1–27. doi: 10.1016/0022-0396(88)90147-7 [14] S. Mungkasi, Variational iteration and successive approximation methods for a SIR epidemic model with constant vaccination strategy, Appl. Math. Model., 2021, 90, 1–10. doi: 10.1016/j.apm.2020.08.058 [15] M. Mandal, S. Jana and S. K. Nandi, A model based study on the dynamics of COVID-19: Prediction and control, Chaos Solit. Fract., 2020, 136, 109889. doi: 10.1016/j.chaos.2020.109889 [16] F. Nazarimehr, V. T. Pham and T. Kapitaniak, Prediction of bifurcations by varying critical parameters of COVID-19, Nonlinear Dyn., 2020, 101, 1681–1692. doi: 10.1007/s11071-020-05749-6 [17] S. S. Nadim and J. Chattopadhyay, Occurrence of backward bifurcation and prediction of disease transmission with imperfect lockdown: a case study on COVID-19, Chaos Solit. Fract., 2020, 140, 110163. doi: 10.1016/j.chaos.2020.110163 [18] A. G. M. Selvam, J. Alzabut and D. A. Vianny, Modeling and stability analysis of the spread of novel coronavirus disease COVID-19, Int. J. Biomath., 2021, 14(5), 2150035. doi: 10.1142/S1793524521500352 [19] A. Viguerie, G. Lorenzo, F. Auricchio, D. Baroli, T. Hughes, A. Pattonm, A. Reali, T. Yankeelov and A. Veneziani, Simulating the spread of COVID-19 via a spatially-resolved susceptible-exposed-infected-recovered-deceased (SEIRD) model with heterogeneous diffusion, Appl. Math. Lett., 2021, 111, 106617. doi: 10.1016/j.aml.2020.106617 [20] P. Yarsky, Using a genetic algorithm to fit parameters of a COVID-19 SEIR model for US states, Math. Comput. Simul., 2021, 185, 687–695. doi: 10.1016/j.matcom.2021.01.022 [21] C. Yang and J. Wang, Transmission rates and environmental reservoirs for COVID-19-a modeling study, J. Biol. Dyn., 2021, 15(1), 86–108. doi: 10.1080/17513758.2020.1869844 [22] L. Zhu, X. Wang, Z. Zhang and C. Lei, Spatial dynamics and optimization method for a rumor propagation model in both homogeneous and heterogeneous environment, Nonlinear Dyn., 2021, 105(4), 3791–3817. doi: 10.1007/s11071-021-06782-9 -
-
-
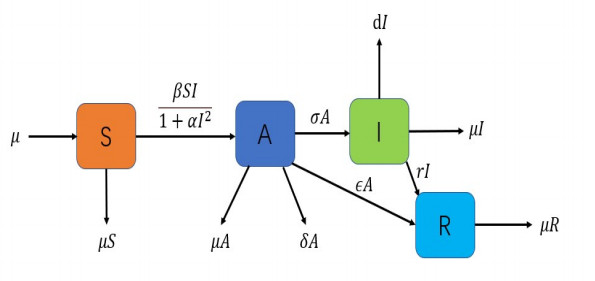
Figure 1.
Scheme diagram of the COVID-19 model (1.1) as diffusion is disappeared.




 DownLoad:
DownLoad: