| Citation: |
Jin Gao, Lihua Dai. ANTI-PERIODIC SYNCHRONIZATION OF CLIFFORD-VALUED NEUTRAL-TYPE CELLULAR NEURAL NETWORKS WITH D OPERATOR[J]. Journal of Applied Analysis & Computation, 2023, 13(5): 2572-2595. doi: 10.11948/20220461
|
ANTI-PERIODIC SYNCHRONIZATION OF CLIFFORD-VALUED NEUTRAL-TYPE CELLULAR NEURAL NETWORKS WITH D OPERATOR
-
Abstract
This paper explores a class of delayed Clifford-valued neutral-type cellular neural networks with $D$ operator. Considering that the multiplication of Clifford algebras does not satisfy the commutativity, by applying the non-decomposition method, Krasnoselskii's Fixed Point Theorem and the proof by contradiction, we obtain several sufficient conditions for the existence and global exponential synchronization of anti-periodic solutions for Clifford-valued neutral-type cellular neural networks with $D$ operator. Finally, we give one example to illustrate the feasibility and effectiveness of the main results.
-
-
References
[1] C. Aouiti, E. Assali and I. Gharbia, Pseudo Almost Periodic Solution of Recurrent Neural Networks with D Operator on Time Scales, Neural Process. Lett., 2019. DOI: 10.1007/s11063-019-10048-2. [2] C. Aouiti and F. Dridi, Weighted pseudo almost automorphic solutions for neutral type fuzzy cellular neural networks with mixed delays and D operator in Clifford algebra, Int. J. Syst. Sci., 2020, 1–23. [3] C. Aouiti, F. Dridi, Q. Hui and E. Moulay, ($\mu$, $\nu$)-Pseudo Almost Automorphic Solutions of Neutral Type Clifford-Valued High-Order Hopfield Neural Networks with D Operator, Neural Process. Lett., 2021, 53, 799–828. doi: 10.1007/s11063-020-10421-6 CrossRef $\mu$,
$\nu$ [4] E. Assali, A spectral radius-based global exponential stability for Clifford-valued recurrent neural networks involving time-varying delays and distributed delays, Comput. Appl. Math., 2023, 42, 48. doi: 10.1007/s40314-023-02188-y [5] S. Ali, M. Usha, Q. Zhu and S. Shanmugam, Synchronization Analysis for Stochastic T-S Fuzzy Complex Networks with Markovian Jumping Parameters and Mixed Time-Varying Delays via Impulsive Control, Math. Probl. Eng., 2020, 1–27. [6] R. Agarwal, S. Grace and D. O'Regan, Oscillation Theory for Difference and Functional Differential Equations, Kluwer Academic, 2020. [7] J. Cao, New results concerning exponential stability and periodic solutions of delayed cellular neural networks, Phys. Lett. A, 2003, 307, 136–147. doi: 10.1016/S0375-9601(02)01720-6 [8] Z. Chen, Global exponential stability of anti-periodic solutions for neutral type CNNs with D operator, Int. J. Mach. Learn. Cyb., 2017. DOI: 10.1007/s13042-016-0633-9. [9] A. Chaouki and F. Touati, Global dissipativity of Clifford-valued multidirectional associative memory neural networks with mixed delays, Comput. Appl. Math., 2020, 39(4), 310–330. doi: 10.1007/s40314-020-01367-5 [10] B. Du, New results on stability of periodic solution for CNNs with proportional delays and D operator, Kybernetika, 2019, 55, 852–869. [11] J. Gao and L. Dai, Anti-Periodic Synchronization of Clifford-Valued Neutral-Type Recurrent Neural Networks With D Operator, IEEE Access, 2022, 10, 9519–9528. doi: 10.1109/ACCESS.2022.3144486 [12] J. Gao and L. Dai, Anti-periodic synchronization of quaternion-valued high-order Hopfield neural networks with delays, AIMS Math., 2022, 7(8), 14051–14075. doi: 10.3934/math.2022775 [13] C. Huang, S. Wen and L. Huang, Dynamics of anti-periodic solutions on shunting inhibitory cellular neural networks with multi-proportional delays, Neurocomputing, 2019, 357, 47–52. doi: 10.1016/j.neucom.2019.05.022 [14] C. Huang, R. Su, J. Cao and S. Xiao, Asymptotically stable of high-order neutral cellular neural networks with proportional delays and D operators, Math. Comput. Simulat., 2019. DOI: 10.1016/j.matcom.2019.06.001. [15] C. Huang, H. Yang and J. Cao, Weighted pseudo almost periodicity of multi-proportional delayed shunting inhibitory cellular neural networks with D operator, Discrete Cont. Dyn. S, 2020, 1259–1272. [16] R. Jia and S. Gong, Convergence of neutral type SICNNs involving proportional delays and D operators, Adv. Differ. Equations, 2018. DOI: 10.1186/s13662-018-1830-5. [17] F. Kong, Q. Zhu, K. Wang and J. Nieto, Stability analysis of almost periodic solutions of discontinuous BAM neural networks with hybrid time-varying delays and D operator, J. Franklin I., 2019. DOI: 10.1016/j.jfranklin.2019.09.030. [18] Y. Li, L. Zhao and X. Chen, Existence of periodic solutions for neutral type cellular neural networks with delays, Appl. Math. Model., 2012, 36, 1173–1183. doi: 10.1016/j.apm.2011.07.090 [19] Y. Li and J. Qin, Existence and global exponential stability of periodic solutions for quaternion-valued cellular neural networks with time-varying delays, Neurocomputing, 2018, 292, 91–103. doi: 10.1016/j.neucom.2018.02.077 [20] Y. Li and J. Xiang, Existence and global exponential stability of anti-periodic solutions for quaternion-valued cellular neural networks with time-varying delays, Adv. Differ. Equations, 2020, 47. [21] Y. Liu, P. Xu, J. Lu and J. Liang, Global stability of Clifford-valued recurrent neural networks with time delays, Nonlinear Dynam., 2016, 84(2), 767–777. doi: 10.1007/s11071-015-2526-y [22] Y. Li and J. Xiang, Existence and global exponential stability of anti-periodic solution for Clifford-valued inertial Cohen-Grossberg neural networks with delays, Neurocomputing, 2018. DOI: 10.1016/j.neucom.2018.12.064. [23] Y. Li and S. Shen, Almost automorphic solutions for Clifford-valued neutral-type fuzzy cellular neural networks with leakage delays on time scales, Neurocomputing, 2020, 417, 23–35. doi: 10.1016/j.neucom.2020.07.035 [24] X. Li, J. Fang and H. Li, Master-slave exponential synchronization of delayed complex-valued memristor-based neural networks via impulsive control, Neural Networks, 2017. DOI: 10.1016/j.neunet.2017.05.008. [25] Y. Li, X. Meng and Y. Ye, Almost Periodic Synchronization for Quaternion-Valued Neural Networks with Time-Varying Delays, Complexity, 2018, 1–13. [26] Y. Li, Y. Fang and J. Qin, Anti-periodic Synchronization of Quaternion-valued Generalized Cellular Neural Networks with Time-varying Delays and Impulsive Effects, Int. J. Control Autom., 2019. DOI: 10.1007/s12555-018-0385-2. [27] G. Peng and L. Huang, Anti-periodic solutions for shunting inhibitory cellular neural networks with continuously distributed delays, Nonlinear Anal. Real., 2009, 10, 2434–2440. doi: 10.1016/j.nonrwa.2008.05.001 [28] L. Peng and W. Wang, Anti-periodic solutions for shunting inhibitory cellular neural networks with time-varying delays in leakage terms, Neurocomputing, 2013, 111, 27–33. doi: 10.1016/j.neucom.2012.11.031 [29] G. Rajchakit, R. Sriraman, N. Boonsatit, P. Hammachukiattikul, C. Lim and P. Agarwal, Global exponential stability of Clifford-valued neural networks with time-varying delays and impulsive effects, Adv. Differ. Equations, 2021. DOI: 10.1186/s13662-021-03367-z. [30] G. Rajchakit, R. Sriramanb, P. Vigneshc and C. Lim, Impulsive effects on Clifford-valued neural networks with time-varying delays: An asymptotic stability analysis, Appl. Math. Comput., 2021, 407, 126309. [31] J. Shao, Anti-periodic solutions for shunting inhibitory cellular neural networks with time-varying delays, Phys. Lett. A, 2008, 372, 5011–5016. doi: 10.1016/j.physleta.2008.05.064 [32] Z. Wang, J. Cao, Z. Cai and L. Rutkowski, Anti-synchronization in fixed time for discontinuous reaction-diffusion neural networks with time-varying coefficients and time delay, IEEE Trans. Cybern, 2019, 50, 2758–276. [33] C. Xu and Y. Wu, Anti-periodic solutions for high-order cellular neural networks with mixed delays and impulses, Adv. Differ. Equations, 2015, 161. [34] C. Xu, Anti-periodic oscillations in fuzzy cellular neural networks with time-varying delays, J. Exp. Theor. Artif. In., 2019, 621–635. [35] C. Xu and P. Li, On anti-periodic solutions for neutral shunting inhibitory cellular neural networks with time-varying delays and D operator, Neurocomputing, 2017. DOI: 10.1016/j.neucom.2017.08.030. [36] Y. Xu, Exponential Stability of Pseudo Almost Periodic Solutions for Neutral Type Cellular Neural Networks with D Operator, Neural Process. Lett., 2017. DOI: 10.1007/s11063-017-9584-8. [37] Z. Xu, X. Li and P. Duan, Synchronization of complex networks with time-varying delay of unknown bound via delayed impulsive control, Neural Networks, 2020. DOI: 10.1016/j.neunet.2020.02.003. [38] L. Yao, Global convergence of CNNs with neutral type delays and D operator, Neural Comput. Appl., 2016. DOI: 10.1007/s00521-016-2403-8. [39] G. Yang and W. Wang, New Results on Convergence of CNNs with Neutral Type Proportional Delays and D Operator, Neural Process. Lett., 2018. DOI: 10.1007/s11063-018-9818-4. [40] K. Yuan, J. Cao and J. Deng, Exponential stability and periodic solutions of fuzzy cellular neural networks with time-varying delays, Neurocomputing, 2006, 69, 1619–1627. doi: 10.1016/j.neucom.2005.05.011 [41] B. Zhang, F. Deng, S. Xie and S. Luo, Exponential synchronization of stochastic time-delayed memristor-based neural networks via distributed impulsive control, Neurocomputing, 2018. DOI: 10.1016/j.neucom.2018.01.051. [42] J. Zhu and J. Sun, Global exponential stability of clifford-valued recurrent neural networks, Neurocomputing, 2015. DOI: 10.1016/j.neucom.2015.08.016. [43] Q. Zhou, Anti-periodic solutions for cellular neural networks with oscillating coefficients in leakage terms, Int. J. Mach. Learn. Cyb., 2017, 8, 1607–1613. doi: 10.1007/s13042-016-0531-1 [44] A. Zhang, Pseudo almost periodic solutions for neutral type SICNNs with D operator, J. Exp. Theor. Artif. In., 2016, 1–13. [45] Q. Zhang, F. Lin, G. Wang and Z. Long, Existence and stability of periodic solutions for stochastic fuzzy cellular neural networks with time-varying delay on time scales, Dynam. Syst. Appl., 2018, 27, 851–871. -
-
Figures(9)
Export File
Citation
Jin Gao, Lihua Dai. ANTI-PERIODIC SYNCHRONIZATION OF CLIFFORD-VALUED NEUTRAL-TYPE CELLULAR NEURAL NETWORKS WITH D OPERATOR[J]. Journal of Applied Analysis & Computation, 2023, 13(5): 2572-2595. doi: 10.11948/20220461
Format
Content
DownLoad:
-
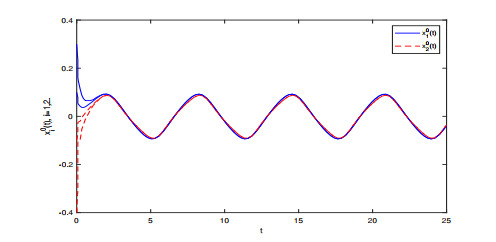
Figure 1.
Transient states of the solutions
$ x_{i}^{0} $ $ i=1, 2 $ -
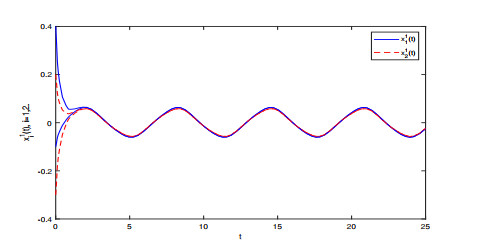
Figure 2.
Transient states of the solutions
$ x_{i}^{1} $ $ i=1, 2 $ -
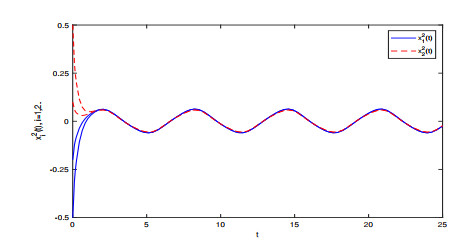
Figure 3.
Transient states of the solutions
$ x_{i}^{2} $ $ i=1, 2 $ -
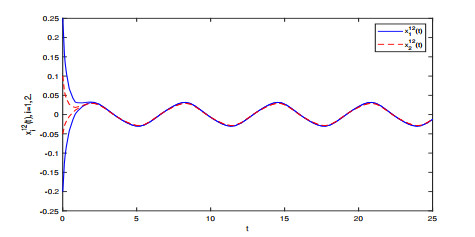
Figure 4.
Transient states of the solutions
$ x_{i}^{12} $ $ i=1, 2 $ -
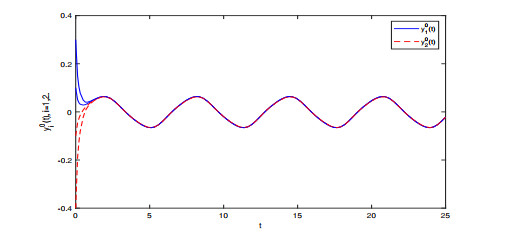
Figure 5.
Transient states of the solutions
$ y_{i}^{0} $ $ i=1, 2 $ -
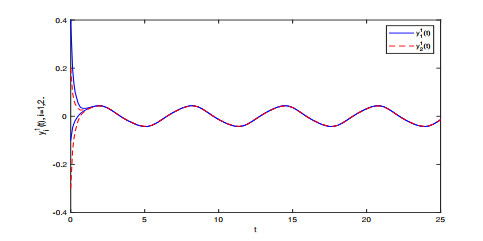
Figure 6.
Transient states of the solutions
$ y_{i}^{1} $ $ i=1, 2 $ -
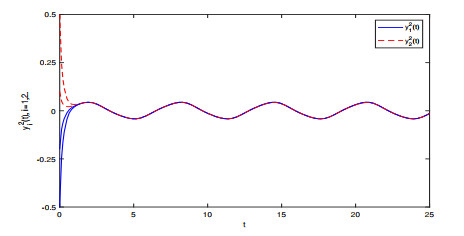
Figure 7.
Transient states of the solutions
$ y_{i}^{2} $ $ i=1, 2 $ -
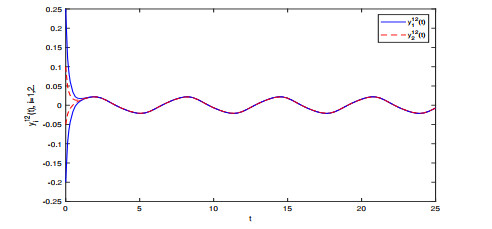
Figure 8.
Transient states of the solutions
$ y_{i}^{12} $ $ i=1, 2 $ -
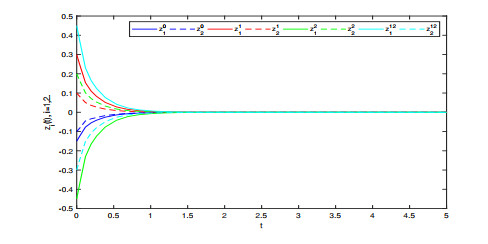
Figure 9.
State response curve of four parts of synchronization error.