| Citation: |
Yanzhi Ma, Zenggui Wang. TRAVELING WAVE SOLUTIONS, POWER SERIES SOLUTIONS AND CONSERVATION LAWS OF THE NONLINEAR DISPERSION EQUATION[J]. Journal of Applied Analysis & Computation, 2023, 13(4): 2267-2282. doi: 10.11948/20220470
|
TRAVELING WAVE SOLUTIONS, POWER SERIES SOLUTIONS AND CONSERVATION LAWS OF THE NONLINEAR DISPERSION EQUATION
-
Abstract
In this paper, the nonlinear dispersive equation is investigated by Lie symmetry analysis theory and bifurcation theory. The infinitesimal generators of the equation are obtained by Lie symmetry analysis. Periodic peakon solutions, single period solutions and power series solutions of the equation are acquired. And the conservation laws are obtained by the Ibragimov's method.
-
-
References
[1] A. R. Adem, Symbolic computation on exact solutions of a coupled Kadomtsev-Petviashvili equation: Lie symmetry analysis and extended tanh method, Comput. Math. with Appl., 2017, 74(8), 1897-1902. doi: 10.1016/j.camwa.2017.06.049 [2] M. A. Abdou, The extended tanh method and its applications for solving nonlinear physical models, Appl. Math. Comput., 2007,190(1), 988-996. [3] M. R. Ali, W. Ma and R. Sadat, Lie Symmetry Analysis and Wave Propagation in Variable-Coefficient Nonlinear Physical Phenomena, East Asian J. Appl. Math., 2022, 12(1), 201-212. doi: 10.4208/eajam.100920.060121 [4] A. Biswas, 1-soliton solution of the equation with generalized evolution, Physics Letters A, 2008,372(25), 4601-4602. doi: 10.1016/j.physleta.2008.05.002 [5] G. Domairry, M. Ahangari and M. Jamshidi, Exact and analytical solution for nonlinear dispersive $K(m,p)$ equations using homotopy perturbation method, Physics Letters A, 2007,368(3-4), 266-270. doi: 10.1016/j.physleta.2007.04.008 CrossRef $K(m,p)$ equations using homotopy perturbation method" target="_blank">Google Scholar
[6] G. Ebadi and A. Biswas, The $(G'/G)$ method and topological soliton solution of the $K(m, n)$ equation, Commun Nonlinear Sci Numer Simul, 2011, 16(6), 2377-2382. doi: 10.1016/j.cnsns.2010.09.009 CrossRef $(G'/G)$ method and topological soliton solution of the
$K(m, n)$ [7] Q. Feng and B. Zheng, Traveling wave solutions for the fifth-order Kdv equation and the BBM equation by $(G'/G)$-expansion method, Wseas Transactions on Mathematics, 2010, 9(3), 171-180. [8] B. Gao and Y. Wang, Invariant Solutions and Nonlinear Self-Adjointness of the Two-Component Chaplygin Gas Equation, Discrete Dyn Nat Soc, 2019, 2019(6), 1-9. [9] M. Inc, Exact and numerical solitons with compact support for nonlinear dispersive $K(m,p)$ equations by the variational iteration method, Physica A, 2007,375(2), 447-456. doi: 10.1016/j.physa.2006.09.033 CrossRef $K(m,p)$ equations by the variational iteration method" target="_blank">Google Scholar
[10] M. S. Ismail and T. R. Taha, A numerical study of compactons, Math Comput Simul, 1998, 47(6), 519-530. doi: 10.1016/S0378-4754(98)00132-3 [11] C. Li, S. Tang and Z. Ma, Analytic and loop solutions for the $K(2,2)$ equation (focusing branch), J. Nonlinear Sci. Appl., 2016, 9(3), 1334-1340. doi: 10.22436/jnsa.009.03.56 CrossRef $K(2,2)$ equation (focusing branch)" target="_blank">Google Scholar
[12] C. Liu, A method of Lie-symmetry $GL(n,R)$ for solving non-linear dynamical systems, Int J Non Linear Mech, 2013, 52, 85-95. doi: 10.1016/j.ijnonlinmec.2013.01.015 CrossRef $GL(n,R)$ for solving non-linear dynamical systems" target="_blank">Google Scholar
[13] S. Li, T. Xia and J. Li, N-soliton solutions of the generalized mixed nonlinear Schrödinger equation through the Riemann-Hilbert method, Modern Physics Letters B, 2022, 36(8), 2150627. doi: 10.1142/S0217984921506272 [14] Z. Li and R. Liu, Bifurcations and Exact Solutions in a Nonlinear Wave Equation, Int J Bifurcat Chaos, 2019, 29(7), 1950098. doi: 10.1142/S0218127419500986 [15] W. Ma, Conservation laws by symmetries and adjoint symmetries, Discrete Contin Dyn Syst Ser A, 2018, 11,707-721. [16] W. Ma, Nonlocal PT-symmetric integrable equations and related Riemann-Hilbert problems, Commun. Partial. Differ. Equ., 2021, 4, 100190. [17] W. Ma, Binary Darboux transformation for general matrix mKdV equations and reduced counterparts, Chaos Solitons Fractals, 2021,146, 110824. doi: 10.1016/j.chaos.2021.110824 [18] W. Ma, Soliton solutions by means of Hirota bilinear forms, Commun. Partial. Differ. Equ., 2022, 5, 100220. [19] W. Ma, Integrable nonlocal nonlinear Schrödinger equations associated with so(3, R), Proceedings of the American Mathematical Society Series B, 2022, 9, 1-11. [20] W. Ma, Reduced Non-Local Integrable NLS Hierarchies by Pairs of Local and Non-Local Constraints, J. Comput. Appl. Math., 2022, 8,206. [21] E. J. Parkes, B. R. Duffy and P. C. Abbort, The Jacobi elliptic-function method for finding periodic-wave solutions to nonlinear evolution equations, Physics Letters A, 2002,295(s5-6), 280-286. [22] P. Rosenau and J. M. Hyman, Compactons: Solitons with finite wavelength, Physical Review Letters, 1993, 70(5), 564-567. doi: 10.1103/PhysRevLett.70.564 [23] H. Triki and A. M. Wazwaz, Soliton solutions for $(2+1)$-dimensional and $(3+1)$-dimensional $K(m,n)$ equations, Appl. Math. Comput., 2010,217(4), 1733-1740. $(2+1)$-dimensional and
$(3+1)$ $K(m,n)$ [24] A. M. Wazwaz, New solitary-wave special solutions with compact support for the nonlinear dispersive $K(m,n)$ equations, Chaos Solitons Fractals, 2002, 13(2), 321-330. doi: 10.1016/S0960-0779(00)00249-6 [25] S. Xie, X. Hong and Y. Tan, Exact Loop Wave Solutions and Cusp Wave Solutions of the Fujimoto-Watanabe Equation, Journal of Nonlinear Modeling and Analysis, 2022, 4(3), 443-453. [26] J. Yang, S. Tian and Z. Li, Riemann-Hilbert method and multi-soliton solutions of an extended modified Korteweg-de Vries equation with N distinct arbitrary-order poles, J. Math. Anal. Appl., 2022,511(2), 126103. doi: 10.1016/j.jmaa.2022.126103 [27] J. Yin and L. Tian, Classification of the travelling waves in the nonlinear dispersive KdV equation, Nonlinear Analysis, 2010, 73(2), 465-470. doi: 10.1016/j.na.2010.03.039 [28] L. Zhang and J. Li, Dynamical behavior of loop solutions for the equation, Physics Letters A, 2011,375(33), 2965-2968. doi: 10.1016/j.physleta.2011.06.040 -
-
Figures(6)
Export File
Citation
Yanzhi Ma, Zenggui Wang. TRAVELING WAVE SOLUTIONS, POWER SERIES SOLUTIONS AND CONSERVATION LAWS OF THE NONLINEAR DISPERSION EQUATION[J]. Journal of Applied Analysis & Computation, 2023, 13(4): 2267-2282. doi: 10.11948/20220470
Format
Content
DownLoad:
-
Figure 1.
phase portraits of (3.5) for
$ {k = 0} $ $ {c>0} $ $ {\beta>0} $ $ {c<0} $ $ {\beta>0} $ $ {c>0} $ $ {\beta<0} $ $ {c<0} $ $ {\beta<0} $ -
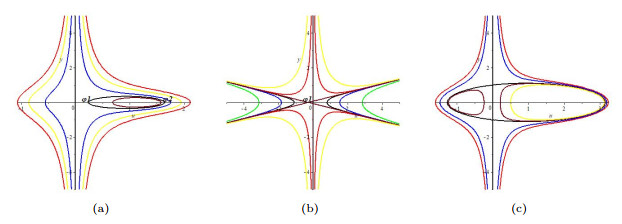
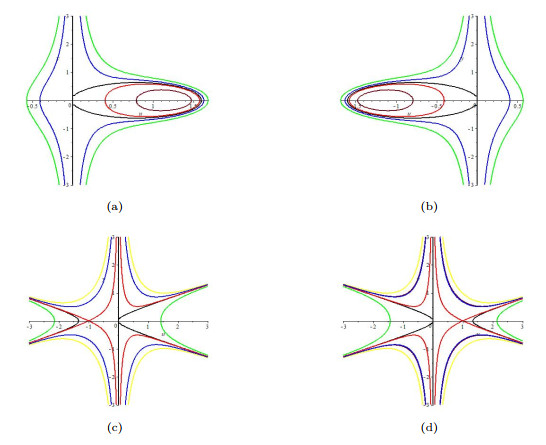
Figure 2.
phase portraits of (3.5) for
$ k\neq0 $ $ c>0 $ $ \beta>0 $ $ -\dfrac{4c^2}{9\beta}<k<0 $ $ \beta<0 $ $ c>0 $ $ k = -\dfrac{4c^2}{9\beta} $ $ \beta>0 $ $ c>0 $ $ k>-\dfrac{4c^2}{9\beta} $ -
Figure 3.
(a) The 3D plot of
$ \psi $ $ \beta>0, $ $ c>0 $ -
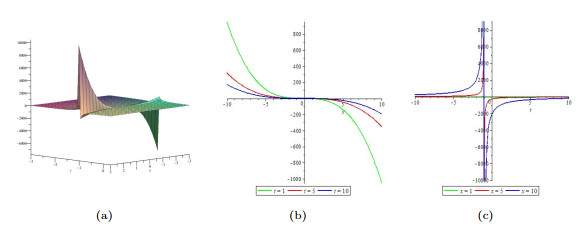
Figure 4.
(a) The 3D plot of
$ \psi $ $ \beta>0, $ $ c>0 $ -
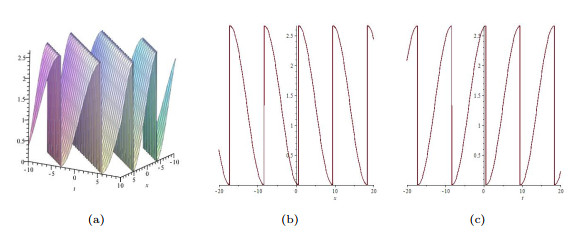
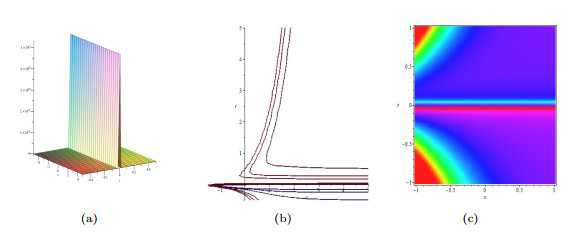
Figure 5.
(a) The 3D plot of
$ \psi $ $ \psi $ $ t = 1 $ $ t = 5 $ $ t = 10 $ $ \psi $ $ x = 1 $ $ x = 5 $ $ x = 10 $ -
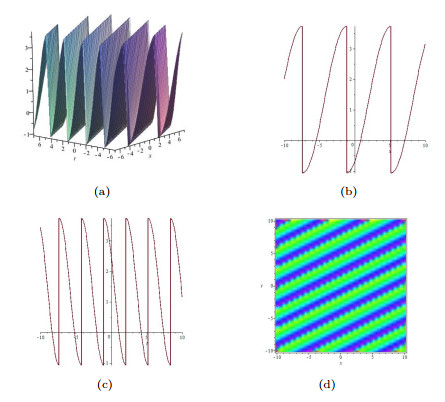
Figure 6.
(a) The 3D plot of
$ \psi $