| Citation: |
Litao Zhang, Yifan Zhang, Xiaojing Zhang, Jianfeng Zhao. A ACCELERATED MODIFIED SHIFT-SPLITTING METHOD FOR NONSYMMETRIC SADDLE POINT PROBLEMS[J]. Journal of Applied Analysis & Computation, 2023, 13(4): 2283-2296. doi: 10.11948/20220473
|
A ACCELERATED MODIFIED SHIFT-SPLITTING METHOD FOR NONSYMMETRIC SADDLE POINT PROBLEMS
-
Abstract
Recently, Huang and Su [A modified shift-splitting method for nonsymmetric saddle, Journal of Computational and Applied Mathematics, 2017,317,535-546] introduced a modified shift-splitting (denoted by MSSP) preconditioner. In this paper, based on modified shift-splitting (denoted by MSSP) iteration technique, we establish a accelerated (named after AMSSP) iterative method for nonsymmetric saddle point problems. Furthermore, we theoretically verify the AMSSP iteration method unconditionally converges to the unique solution of the saddle point problems, compute the spectral radius of the AMSSP iteration matrix. Finally, numerical examples show the spectrum of the new preconditioned matrix for the different parameters.
-
Keywords:
- Saddle point problem /
- shift-splitting /
- Krylov subspace methods /
- convergence rate /
- preconditioner
-
-
References
[1] Z. Bai and L. Zhang, Modulus-based synchronous multisplitting iteration methods for linear complementarity problems, Numerical Linear Algebra with Applications, 2013, 20,425-439. doi: 10.1002/nla.1835 [2] Z. Bai, On the convergence of the multisplitting methods for the linear complementarity problem, SIAM Journal on Matrix Analysis and Applications, 1999, 21, 67-78. doi: 10.1137/S0895479897324032 [3] Z. Bai, The convergence of parallel iteration algorithms for linear complementarity problems, Computers and Mathematics with Applications, 1996, 32, 1-17. [4] Z. Bai and D. J. Evans, Matrix multisplitting relaxation methods for linear complementarity problems, International Journal of Computer Mathematics, 1997, 63,309-326. doi: 10.1080/00207169708804569 [5] Z. Bai, On the monotone convergence of matrix multisplitting relaxation methods for the linear complementarity problem, IMA Journal of Numerical Analysis, 1998, 18,509-518. doi: 10.1093/imanum/18.4.509 [6] Z. Bai and D. J. Evans, Matrix multisplitting methods with applications to linear complementarity problems: parallel synchronous and chaotic methods, Reseaux et systemes repartis: Calculateurs Paralleles, 2001, 13,125-154. [7] Z. Bai, Modulus-based matrix splitting iteration methods for linear complementarity problems, Numerical Linear Algebra with Applications, 2010, 17,917-933. doi: 10.1002/nla.680 [8] Z. Bai and L. Zhang, Modulus-based synchronous two-stage multisplitting iteration methods for linear complementarity problems, Numerical Algorithms, 2013, 62, 59-77. doi: 10.1007/s11075-012-9566-x [9] Z. Bai and D. J. Evans, Matrix multisplitting methods with applications to linear complementarity problems: parallel asynchronous methods, International Journal of Computer Mathematics, 2002, 79,205-232. doi: 10.1080/00207160211927 [10] Z. Bai, Parallel matrix multisplitting block relaxation iteration methods, Mathematica Numerica Sinica, 1995, 3,238-252. doi: 10.12286/jssx.1995.3.238 [11] A. Berman and R. J. Plemmons, Nonnegative Matrices in the Mathematical Sciences, Academic Press: New York, 1979. [12] L. Cui, X. Zhang and S. Wu, A new preconditioner of the tensor splitting iterative method for solving multi-linear systems with $\mathcal{M}$-tensors, Computers and Mathematics with Applications, 2020, 39,173. https://doi.org/10.1007/s40314-020-01194-8. doi: 10.1007/s40314-020-01194-8 CrossRef $\mathcal{M}$-tensors" target="_blank">Google Scholar
[13] L. Cui, M. Li and Y. Song, Preconditioned tensor splitting iterations method for solving multi-linear systems, Applied Mathematics Letters, 2019, 96, 89-94. doi: 10.1016/j.aml.2019.04.019 [14] R. W. Cottle, J. Pang and R. E. Stone, The Linear Complementarity Problem, Academic Press, San Diego, 1992. [15] J. Dong and M. Jiang, A modified modulus method for symmetric positive-definite linear complementarity problems, Numerical Linear Algebra with Applications, 2009, 16,129-143. doi: 10.1002/nla.609 [16] M. C. Ferris and J. Pang, Engineering and economic applications of complementarity problems, SIAM Review, 1997, 39,669-713. doi: 10.1137/S0036144595285963 [17] A. Frommer and G. Mayer, Convergence of relaxed parallel multisplitting methods, Linear Algebra and Its Applications, 1989,119,141-152. doi: 10.1016/0024-3795(89)90074-8 [18] A. Hadjidimos, M. Lapidakis and M. Tzoumas, On Iterative Solution for Linear Complementarity Problem with an $H_{+}$-Matrix, SIAM Journal on Matrix Analysis and Applications, 2012, 33, 97-110. doi: 10.1137/100811222 [19] A. Hadjidimos and M. Tzoumas, Nonstationary extrapolated modulus algorithms for the solution of the linear complementarity problem, Linear Algebra and Its Applications, 2009,431,197-210. doi: 10.1016/j.laa.2009.02.024 [20] D. Jiang, W. Li and H. Lv, An energy-efficient cooperative multicast routing in multi-hop wireless networks for smart medical applications, Neurocomputing, 2017,220,160-169. doi: 10.1016/j.neucom.2016.07.056 [21] D. Jiang, Y. Wang, Y. Han and H. Lv, Maximum connectivity-based channel allocation algorithm in cognitive wireless networks for medical applications, Neurocomputing, 2017,220, 41-51. doi: 10.1016/j.neucom.2016.05.102 [22] D. Jiang, Z. Xu, W. Li, et al., An energy-efficient multicast algorithm with maximum network throughput in multi-hop wireless networks, Journal of Communications and Networks, 2016, 18(5), 713-724. doi: 10.1109/JCN.2016.000101 [23] D. Jiang, Z. Xu, J. Liu and W. Zhao, An optimization-based robust routing algorithm to energy-efficient networks for cloud computing, Telecommunication Systems, 2016, 63(1), 89-98. doi: 10.1007/s11235-015-9975-y [24] D. Jiang, Z. Xu and Z. Lv, A multicast delivery approach with minimum energy consumption for wireless multi-hop networks, Telecommunication Systems, 2016, 62(4), 771-782. doi: 10.1007/s11235-015-0111-9 [25] D. Jiang, L. Nie, Z. Lv and H. Song, Spatio-temporal Kronecker compressive sensing for traffic matrix recovery, IEEE Access, 2016, 4, 3046-3053. doi: 10.1109/ACCESS.2016.2573264 [26] W. Li, A general modulus-based matrix splitting method for linear complementarity problems of H-matrices, Applied Mathematics Letters, 2013, 26, 1159-1164. doi: 10.1016/j.aml.2013.06.015 [27] Y. Li, X. Wang and C. Sun, Convergence analysis of linear complementarity problems based on synchronous block multisplitting iteration methods, Journal of Nanchang University, Natural Science, 2013, 37,307-312. [28] F. Robert, M. Charnay and F. Musy, Iterations chaotiques serie-parallel pour des equations non-lineaires de point fixe, Matematiky, 1975, 20, 1-38. [29] Y. Song, Convergence of Block AOR Iterative Methods, Mathematica Applicata, 1993, 1, 39-45. [30] R. S. Varga, Matrix Iterative Analysis, Springer-Verlag, Berlin and Heidelberg, 2000. [31] W. M. G. van Bokhoven, Piecewise-Linear Modelling and Analysis, Proefschrift, Eindhoven, 1981. [32] D. M. Young, Iterative Solution of Large Linear Systems, Academic Press, New York, 1972. [33] L. Zhang and Z. Ren, Improved convergence theorems of modulus-based matrix splitting iteration methods for linear complementarity problems, Applied Mathematics Letters, 2013, 26,638-642. doi: 10.1016/j.aml.2013.01.001 [34] L. Zhang, T. Huang, S. Cheng and T. Gu, The weaker convergence of non-stationary matrix multisplitting methods for almost linear systems, Taiwanese Journal of Mathematics, 2011, 15, 1423-1436. [35] L. Zhang and J. Li, The weaker convergence of modulus-based synchronous multisplitting multi-parameters methods for linear complementarity problems, Computers and Mathematics with Application, 2014, 67, 1954-1959. doi: 10.1016/j.camwa.2014.04.018 [36] L. Zhang, T. Huang and T. Gu, Global relaxed non-stationary multisplitting multi-parameters methods, International Journal of Computer Mathematics, 2008, 85,211-224. doi: 10.1080/00207160701405451 [37] L. Zhang, T. Huang, T. Gu and X. Guo, Convergence of relaxed multisplitting USAOR method for an H-matrix, Applied Mathematics and Computation, 2008,202,121-132. doi: 10.1016/j.amc.2008.01.034 [38] L. Zhang, T. Huang and T. Gu, Convergent improvement of SSOR multisplitting method, Journal of Computational and Applied Mathematics, 2009,225,393-397. doi: 10.1016/j.cam.2008.07.051 [39] L. Zhang, T. Huang, S. Cheng, T. Gu and Y. Wang, A note on parallel multisplitting TOR method of an H-matrix, International Journal of Computer Mathematics, 2011, 88,501-507. doi: 10.1080/00207160903501917 [40] L. Zhang, X. Zuo, T. Gu and X. Liu, Improved convergence theorems of multisplitting methods for the linear complementarity problem, Applied Mathematics and Computation, 2014,243,982-987. doi: 10.1016/j.amc.2014.06.038 [41] L. Zhang, J. Li, T. Gu and X. Liu, Convergence of relaxed matrix multisplitting chaotic methods for H-matrices, Journal of Applied Mathematics, 2014, 2014, 9. [42] L. Zhang, Y. Zhou, T. Gu and X. Liu, Convergence improvement of relaxed multisplitting USAOR methods for H-matrices linear systems, Applied Mathematics and Computation, 2014,247,225-232. doi: 10.1016/j.amc.2014.08.106 -
-
Figures(7) / Tables(4)
Export File
Citation
Litao Zhang, Yifan Zhang, Xiaojing Zhang, Jianfeng Zhao. A ACCELERATED MODIFIED SHIFT-SPLITTING METHOD FOR NONSYMMETRIC SADDLE POINT PROBLEMS[J]. Journal of Applied Analysis & Computation, 2023, 13(4): 2283-2296. doi: 10.11948/20220473
Format
Content
DownLoad:
-
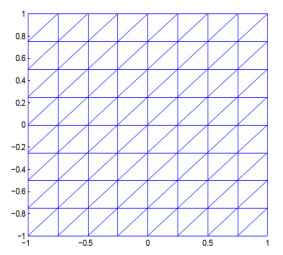
Figure 1.
A uniform mesh with
$ h = \frac{\sqrt{2}}{4} $ -
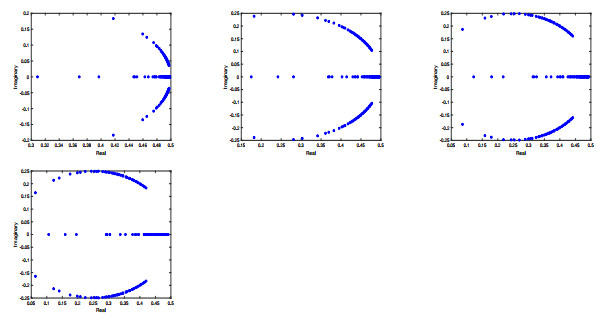
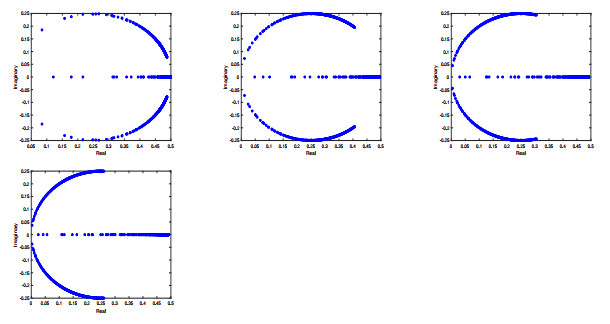
Figure 2.
The eigenvalue distribution for the block preconditioned matrix
$\mathcal{P}_{\alpha}^{-1}A$ $\alpha = 0.1$ $\alpha = 0.3$ $\alpha = 0.5$ $\alpha = 0.6$ $h = \frac{\sqrt{2}}{8}$ -
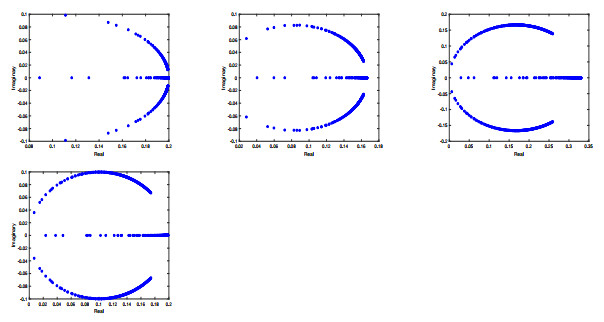
Figure 3.
The eigenvalue distribution for the block preconditioned matrix
$\mathcal{P}_{\alpha,\beta}^{-1}A$ $\alpha = 0.1,\beta = 5$ $\alpha = 0.3,\beta = 6$ $\alpha = 0.5,\beta = 3$ $\alpha = 0.6,\beta = 5$ $h = \frac{\sqrt{2}}{8}$ -
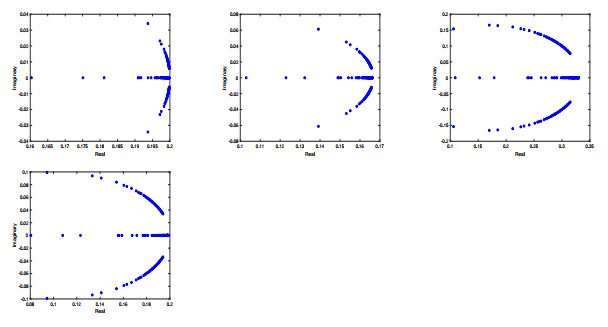
Figure 4.
The eigenvalue distribution for the block preconditioned matrix
$\mathcal{P}_{\alpha}^{-1}A$ $\alpha = 0.1$ $\alpha = 0.3$ $\alpha = 0.5$ $\alpha = 0.6$ $h = \frac{\sqrt{2}}{12}$ -
Figure 5.
The eigenvalue distribution for the block preconditioned matrix
$\mathcal{P}_{\alpha,\beta}^{-1}A$ $\alpha = 0.1,\beta = 5$ $\alpha = 0.3,\beta = 6$ $\alpha = 0.5,\beta = 3$ $\alpha = 0.6,\beta = 5$ $h = \frac{\sqrt{2}}{12}$ -
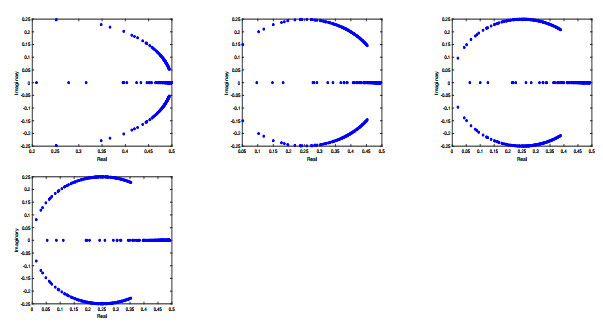
Figure 6.
The eigenvalue distribution for the block preconditioned matrix
$\mathcal{P}_{\alpha}^{-1}A$ $\alpha = 0.1$ $\alpha = 0.3$ $\alpha = 0.5$ $\alpha = 0.6$ $h = \frac{\sqrt{2}}{18}$ -
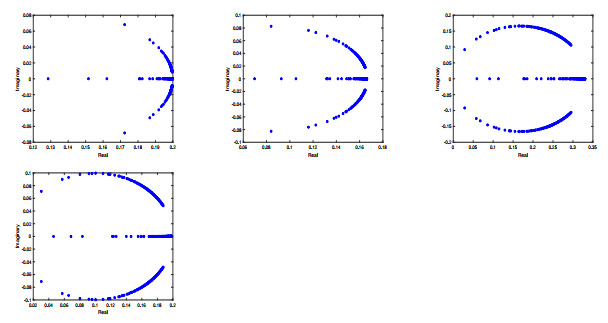
Figure 7.
The eigenvalue distribution for the block preconditioned matrix
$\mathcal{P}_{\alpha,\beta}^{-1}A$ $\alpha = 0.1,\beta = 5$ $\alpha = 0.3,\beta = 6$ $\alpha = 0.5,\beta = 3$ $\alpha = 0.6,\beta = 5$ $h = \frac{\sqrt{2}}{18}$