| Citation: | Sh. Zhagharian, M. H. Heydari, M. Razzaghi. A NUMERICAL METHOD FOR TWO-DIMENSIONAL DISTRIBUTED-ORDER FRACTIONAL NONLINEAR SOBOLEV EQUATION[J]. Journal of Applied Analysis & Computation, 2023, 13(5): 2630-2645. doi: 10.11948/20220480 |
A NUMERICAL METHOD FOR TWO-DIMENSIONAL DISTRIBUTED-ORDER FRACTIONAL NONLINEAR SOBOLEV EQUATION
-
Abstract
This study introduces the distributed-order fractional version of the nonlinear two-dimensional Sobolev equation. The orthonormal Chebyshev cardinal polynomials are used to construct a numerical method for this equation. To this end, some derivative matrices related to these polynomials are obtained. The proposed approach turns to solve this equation into solving a nonlinear system of algebraic equations by approximating the unknown solution using the expressed polynomials and employing their derivative matrices. The applicability and validity of this method are examined by solving three examples.
-

-
References
[1] T. M. Atanackovic, A generalized model for the uniaxial isothermal deformation of a viscoelastic body, Acta Mechanica, 2002, 159(1), 77–86. [2] M. Abbaszadeh, Error estimate of second-order finite difference scheme for solving the Riesz space distributed-order diffusion equation, Applied Mathematics Letters, 2019, 88, 179–185. doi: 10.1016/j.aml.2018.08.024 [3] O. Bavi, M. Hosseininia, M. H. Heydari and N. Bavi, SARS-CoV-2 rate of spread in and across tissue, groundwater and soil: A meshless algorithm for the fractional diffusion equation, Engineering analysis with boundary elements, 2022, 138, 108–117. doi: 10.1016/j.enganabound.2022.01.018 [4] C. Canuto, M. Y. Hussaini, A. Quarteroni and T. Zang, Spectral methods: fundamentals in single domains, Springer Science & Business Media, 2007. [5] M. H. Derakhshan and A. Aminataei, A numerical method for finding solution of the distributed-order time-fractional forced Korteweg-de Vries equation including the Caputo fractional derivative, Mathematical Methods in the Applied Sciences, 2022, 45(5), 3144–3165. doi: 10.1002/mma.7981 [6] R. E. Ewing, Numerical solution of Sobolev partial differential equations, SIAM Journal on Numerical Analysis, 1975, 12(3), 345–363. doi: 10.1137/0712028 [7] S. Haq and I. Ali, Approximate solution of two-dimensional Sobolev equation using a mixed Lucas and Fibonacci polynomials, Engineering with Computers, 2022, 38(3), 2059–2068. [8] M. Hosseininia, M. H. Heydari and Z. Avazzadeh, A hybrid approach established upon the Müntz-Legender functions and 2D Müntz-Legender wavelets for fractional Sobolev equation, Mathematical Methods in the Applied Sciences, 2022, 45(9), 5304–5320. doi: 10.1002/mma.8107 [9] M. H. Heydari and A. Atangana, An accurate approach based on the orthonormal shifted discrete Legendre polynomials for variable-order fractional Sobolev equation, Advances in Difference Equations, 2021, 2021(1), 1–12. doi: 10.1186/s13662-020-03162-2 [10] M. H. Heydari and A. Atangana, A cardinal approach for nonlinear variable-order time fractional Schrödinger equation defined by Atangana-Baleanu-Caputo derivative, Chaos, Solitons and Fractals, 2019, 128, 339–348. doi: 10.1016/j.chaos.2019.08.009 [11] M. H. Heydari and Z. Avazzadeh, A direct computational method for nonlinear variable-order fractional delay optimal control problems, Asian Journal of Control, 2021, 23(6), 2709–2718. doi: 10.1002/asjc.2408 [12] M. H. Heydari and M. Razzaghi, Third-kind Chebyshev cardinal functions for variable-order time fractional RLW-Burgers equation, Mathematical Methods in the Applied Sciences, 2022, 45(10), 5670–5681. doi: 10.1002/mma.8133 [13] M. H. Heydari and M. Razzaghi, Piecewise Chebyshev cardinal functions: Application for constrained fractional optimal control problems, Chaos, Solitons and Fractals, 2021, 150, 111118. doi: 10.1016/j.chaos.2021.111118 [14] M. H. Heydari, A. Atangana, Z. Avazzadeh and Y. Yang, Numerical treatment of the strongly coupled nonlinear fractal-fractional Schrödinger equations through the shifted Chebyshev cardinal functions, Alexandria Engineering Journal, 2020, 59(4), 2037–2052. doi: 10.1016/j.aej.2019.12.039 [15] F. B. Hildebrand, Introduction to numerical analysis, Courier Corporation, 1987. [16] N. Jibenja, B. Yuttanan and M. Razzaghi, An efficient method for numerical solutions of distributed-order fractional differential equations, Journal of Computational and Nonlinear Dynamics, 2018, 13(11), 10. [17] S. Kumar and A. Atangana, Numerical solution of ABC space-time fractional distributed order reaction-diffusion equation, Numerical methods for partial differential equations, 2022, 38(3), 406–421. [18] J. Liu, H. Li and Y. Liu, Crank-Nicolson finite element scheme and modified reduced-order scheme for fractional Sobolev equation, Numerical Functional Analysis and Optimization, 2018, 39(15), 1635–1655. doi: 10.1080/01630563.2018.1488143 [19] D. Liu, Y. Tian, D. Boutat and T. M. Laleg-Kirati, An algebraic fractional order differentiator for a class of signals satisfying a linear differential equation, Signal Processing, 2015, 116, 78–90. doi: 10.1016/j.sigpro.2015.04.017 [20] Y. Luchko, Boundary value problems for the generalized time-fractional diffusion equation of distributed order, Fractional Calculus and Applied Analysis, 2009, 12(4), 409–422. [21] N. Moshtaghi and A. Saadatmandi, Polynomial-sinc collocation method combined with the Legendre-Gauss quadrature rule for numerical solution of distributed order fractional differential equations, Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas, 2021, 115(2), 1–23. [22] M. Naber, Distributed order fractional sub-diffusion, Fractals, 2004, 12(01), 23–32. doi: 10.1142/S0218348X04002410 [23] K. B. Oldham, Fractional differential equations in electrochemistry, Advances in Engineering software, 2010, 41(1), 9–12. doi: 10.1016/j.advengsoft.2008.12.012 [24] I. Podlubny, Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications, Elsevier, 1998. [25] M. Pourbabaee and A. Saadatmandi, A new operational matrix based on Müntz-Legendre polynomials for solving distributed order fractional differential equations, Mathematics and Computers in Simulation, 2022, 194, 210–235. doi: 10.1016/j.matcom.2021.11.023 [26] J. Rouzegar, M. Vazirzadeh and M. H. Heydari, A fractional viscoelastic model for vibrational analysis of thin plate excited by supports movement, Mechanics Research Communications, 2020, 110, 103618. doi: 10.1016/j.mechrescom.2020.103618 [27] J. Rashidinia, T. Eftekhari and K. Maleknejad, A novel operational vector for solving the general form of distributed order fractional differential equations in the time domain based on the second kind Chebyshev wavelets, Numerical Algorithms, 2021, 88(4), 1617–1639. doi: 10.1007/s11075-021-01088-8 [28] B. Yuttanan, M. Razzaghi and T. N. Vo, A numerical method based on fractional-order generalized Taylor wavelets for solving distributed-order fractional partial differential equations, Communications in Nonlinear Science and Numerical Simulation, 2021, 160, 349–367. [29] M. A. Zaky and J. A. Tenreiro Machado, On the formulation and numerical simulation of distributed order fractional optimal control, Communications in Nonlinear Science and Numerical Simulation, 2017, 52, 177–189. doi: 10.1016/j.cnsns.2017.04.026 [30] M. A. Zaky and J. A. Tenreiro Machado, On the formulation and numerical simulation of distributed-order fractional optimal control problems, Communications in Nonlinear Science and Numerical Simulation, 2017, 52, 177–189. doi: 10.1016/j.cnsns.2017.04.026 [31] J. Zhao, Z. Fang, H. Li and Y. Liu, A Crank-Nicolson finite volume element method for time fractional sobolev equations on triangular grids, Mathematics, 2020, 8(9), 1591. doi: 10.3390/math8091591 [32] D. Zhao and Q. Zhang, Local discontinuous Galerkin methods with generalized alternating numerical fluxes for two-dimensional linear Sobolev equation, Journal of Scientific Computing, 2019, 78(3), 1660–1690. -
-
-
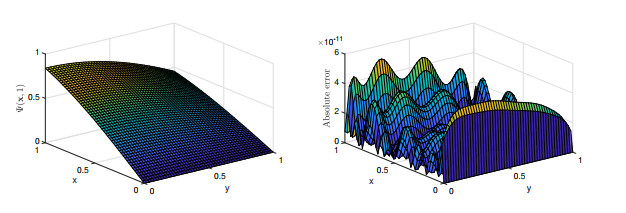
Figure 1.
The outcomes obtained for
$ \Psi({\mathbf{x}}, 1) $ $ m=n=q=8 $ -
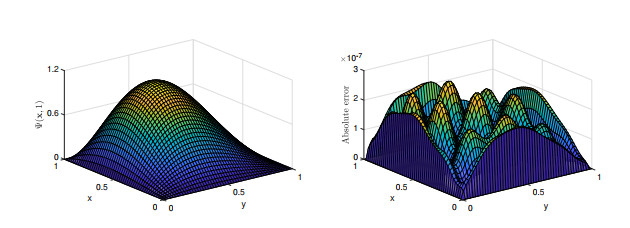
Figure 2.
The outcomes obtained for
$ \Psi({\mathbf{x}}, 1) $ $ m=n=8, q=7 $ -
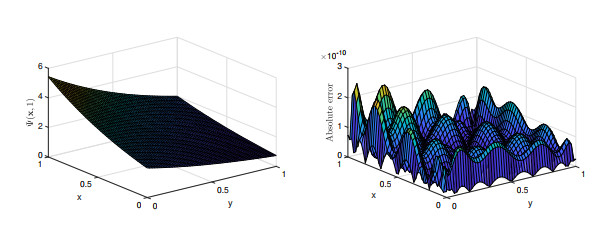
Figure 3.
The outcomes obtained for
$ \Psi({\mathbf{x}}, 1) $ $ m=n=9, q=8 $




 DownLoad:
DownLoad: