| Citation: |
Ronghua Wang, Beiqing Gu, Xiaoling Xu, Shu-Yi Zhang. STUDY OF A GENERALIZED WEIBULL DISTRIBUTION WITH OSCILLATORY FAILURE RATE[J]. Journal of Applied Analysis & Computation, 2023, 13(4): 2326-2342. doi: 10.11948/20220544
|
STUDY OF A GENERALIZED WEIBULL DISTRIBUTION WITH OSCILLATORY FAILURE RATE
-
Abstract
A four-parameter life distribution $ \text{ORS}(\lambda,A,m,\beta) $ with oscillatory failure rate is given, which can be regarded as a generalization of the Weibull distribution. For the three-parameter oscillation type distribution $ \text{ORS}(A,m,\beta) $, the image characteristics of the failure rate are theoretically proved, and the parameter estimation method is given in the whole sample case. Finally, the paper illustrates the feasibility of the method by simulating and practical examples.
-
Keywords:
- Density function /
- failure rate /
- lifetime distribution /
- oscillating type /
- parameter estimation
-
-
References
[1] M. A. Aldahlam, F. Jamal, C. Chesneau, Ibrahim Elbatal, Mohamment EIgarhy. Exponentiated power generalized Weibull power series family of distributions: Properties, estimation and applications, PLOS ONE, 2020, 15(3), 1–25. [2] A. Amirzadi, E. Baloui Jamkhaneh, E. Deiri, A comparison of estimation methods for reliability function of inverse generalized Weibull distribution under new loss function, Journal of Statistical Computation and Simulation, 2021, 91(13), 2592–2622. [3] V. M. Areyushenko, V. I. Volovach, Estimation of Motion Intensity of Extended Objects Using Generalized Weibull Distribution, Optoelectronics Instrumentation and Data Processing, 2020, 56(3), 261–268. doi: 10.3103/S8756699020030024 [4] G. Aryal, C. Tsokos, Transmuted Weibull distribution: A generalization of the Weibull Probability distribution, European Journal of Pure and Applied Mathematics, 2011, 4(2), 89–102. [5] M. Bebbington, C. -D. Lai, R. Zitikis, A flexible Weibull extension, Reliability Engineering and System Safety, 2007, 92, 719–726. doi: 10.1016/j.ress.2006.03.004 [6] L. Bekker, J. Mi, Shape an crossing properties of mean residual life functions, Statistics & Probability Letters, 2003, 64, 225–234. [7] J. B. Chakraabarty, S. Chowdhury, Compounded generalized Weibull distributions - A unified approach, Journal of Statistics and Management Systems, 2020, 23(5), 887–913. doi: 10.1080/09720510.2019.1677315 [8] Z. Chen, A new two-parameter lifetime distribution with bathtub shape or increasing failure rate function, Statistics and Probability Letters, 2002, 49, 155–161. [9] G. M. Cordeirv, E. M. M. Ortega, T. G. Ramires, A new generalized Weibull family of distribution: mathematical properties and applications, Journal of Statistical Distributions and Applications, 2015, 2, 13. doi: 10.1186/s40488-015-0036-6 [10] M. R. Gurvieh, A. T. Dibenedetto, S. V. Rande, A new statistical distribution for characterizing the random strength of brittle materials, Journal of Materials Science, 1997, 32, 2559–2564. doi: 10.1023/A:1018594215963 [11] H. Hecht, E. Fiorentio, Reliability assessment of spacecraft electronics, Proceedings of the Annual Reliability and Maintainability Symposium, January 1987. [12] M. C. Jones, A. Noufaily, K. Burke, A bivariate power generalized Weibull distribution: A flexible parametric model for survival analysis, Statistical Methods in Medical Research, 2020, 29(8), 2295–2306. doi: 10.1177/0962280219890893 [13] Z. Kang, X. Yao, Experimental research on piston oscillating behavior of fluid in a moonpool with wave-flow, Journal of Harbin Engineering University, 2008, 29(3), 209–216. doi: 10.3969/j.issn.1006-7043.2008.03.002 [14] M. Khan, R. King, I. Hudson, Transmuted modified Weibull distribution: Properties and application, European Journal of Pure and Applied Mathematics, 2013, 6(1), 66–88. [15] C. D. Lai, M. Xie, D. N. P. Murthy, Modified Weibull model, IEEE Transactions on Reliability, 2003, 52(1), 33–37. doi: 10.1109/TR.2002.805788 [16] Y. Liu, S. Zhao, Z. Zhao, et al., Life distribution model of products with variable probability density of Exponential attenuation oscillation, Journal of Nanjing University of Aeronautics and Astronautics, 2021, 53(3), 449–454. [17] S. Mirzaei, G. R. Mohtashami Borzadaran, M. Amini, H. Jabbari, A new generalized Weibull distribution in income economic inequality curves, Communications in Statistics-Theory and Methods, 2019, 48(4), 889–908. doi: 10.1080/03610926.2017.1422754 [18] G. S. Mudholkar, D.K. Srivastava, Exponentiated Weibull Family for Analyzing Bathtub Failure Rate Data, IEEE Transactions on Reliability, 1993, 42(2), 299–302. doi: 10.1109/24.229504 [19] S. Nadarajah, S. Kotz, On some recent modifications of Weibull distribution, IEEE Transactions on Reliability, 2005, 54(4), 561–562. doi: 10.1109/TR.2005.858811 [20] S. Nadarajah, E. Ortega, The exponentiated Weibull distribution: a survey, Statistical Papers, 2013, 54(3), 839–877. doi: 10.1007/s00362-012-0466-x [21] R. Pandey, N. Kumari, Bayesian Analysis of Power Generalized Weibull Distribution, International Journal of Applied and Computational Mathematics, 2018, 4, 141. [22] X. Peng, An extended Weibull model with variable periodicity, Journal of Systems Science and Complexity, 2018, 31, 841–858. doi: 10.1007/s11424-018-7046-7 [23] B. Singh, R. U. Khan, M. A. Khan, Characterizations of q-Weibull distribution based on generalized order statistics, Journal of Statistics and Management Systems, 2019, 22(8), 1573–1595. doi: 10.1080/09720510.2019.1643554 [24] N. Singla, K. Jain, S. K. Sharma, The Beta Generalized Weibull distribution: properties and applications, Reliability Engineering and System Safety, 2012, 102, 5–15. doi: 10.1016/j.ress.2012.02.003 [25] D. Sun, P. Liu, F. Tong, Effect of spanwise oscillation on interaction of shock wave and turbulent boundary layer, Acta Aeronautica et Astronautica Sinica, 2020, 41(12), 54–66. [26] L. C. Tang, Y. Lu, E. P. Chew, Mean residual life of lifetime distributions, IEEE Transactions on Reliability, 1999, 48(1), 73–78. doi: 10.1109/24.765930 [27] W. Weibill, A statistical distribution of wide applicability, Journal of Applied Mechanics, 1951, 18, 293–297. doi: 10.1115/1.4010337 [28] K. L. Wong, The bathtub does not hold water any more, Quality and Reliability Engineering International, 1988, 4(3), 279–282. doi: 10.1002/qre.4680040311 [29] K. L. Wong, The roller-coaster curve is in, Quality and Reliability Engineering International, 1989, 5(1), 29–36. [30] K. L. Wong, The physical basis for the roller-coaster hazard rate for electronics, Quality and Reliability Engineering International, 1991, 7(6), 489–495. [31] J. W. Wu, H. L. Lu, C. H. Chen, et al. Statistical inference about the shape parameter of the new-parameter bathtub-shaped lifetime distribution, Quality and Reliability Engineering International, 2004, 20, 607–616. [32] M. Xie, Y. Tang, T. N. Goh, A modified Weibull extension with bathtub-shaped failure rate function, Reliability Engineering & System Safety, 2002, 76, 279–285. [33] Z. Zhang, S. Nadarajah, A note on "Parameter estimation for bivariate Weibull distribution using generalized moment method for reliability evaluation", Quality and Reliability Engineering International, 2019, 35, 730–735. -
-
Figures(15)
Export File
Citation
Ronghua Wang, Beiqing Gu, Xiaoling Xu, Shu-Yi Zhang. STUDY OF A GENERALIZED WEIBULL DISTRIBUTION WITH OSCILLATORY FAILURE RATE[J]. Journal of Applied Analysis & Computation, 2023, 13(4): 2326-2342. doi: 10.11948/20220544
Format
Content
DownLoad:
-
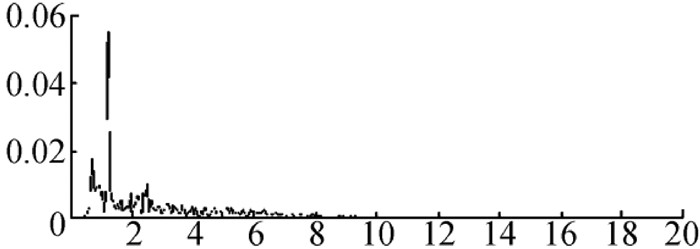
Figure 1.
Wave high power spectral density function plot with wave height of 60mm, period of 1.5s and flow rate of 2.0m/s
-
Figure 2.
Hydrophone signal power spectral density function diagram with wave height of 60mm, period of 1.5s and flow rate of 2.0m/s
-
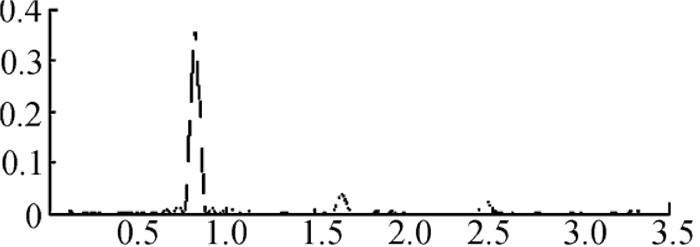
Figure 3.
Wave high power spectral density function plot with wave height of 60mm, period of 2s and flow rate of 2.0m/s
-
Figure 4.
Hydrophone signal power spectral density function diagram with wave height of 60mm, period of 2s and flow rate of 2.0m/s
-
Figure 5.
Density function of surface tangent stress angle
-
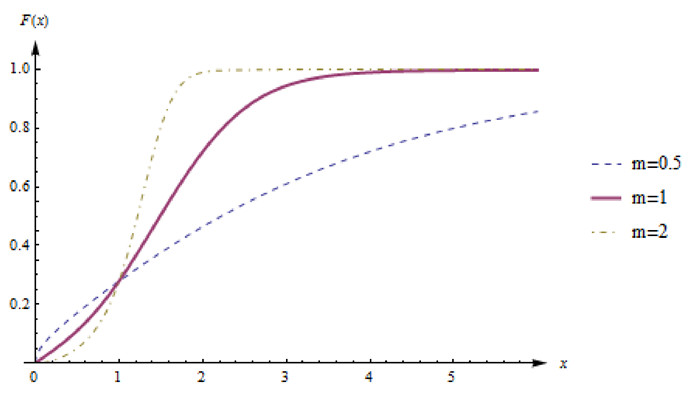
Figure 6.
Image of distribution function
$ F(x) $ $ A=0.8 $ -
Figure 7.
Image of the distribution function
$ F(x) $ $ A=-0.8 $ -
Figure 8.
Image of the density function
$ f(x) $ $ A=0.8 $ -
Figure 9.
Image of the density function
$ f(x) $ $ A=-0.8 $ -
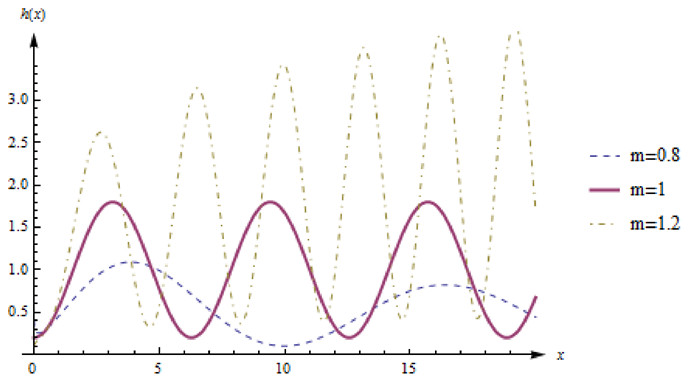
Figure 10.
Image of the failure rate function
$ h(x) $ $ A=0.8 $ -
Figure 11.
Image of the failure rate function
$ h(x) $ $ A=-0.8 $ -
Figure 12.
Image of the function
$ G(A) $ $ A=-1(0.05)1 $ -
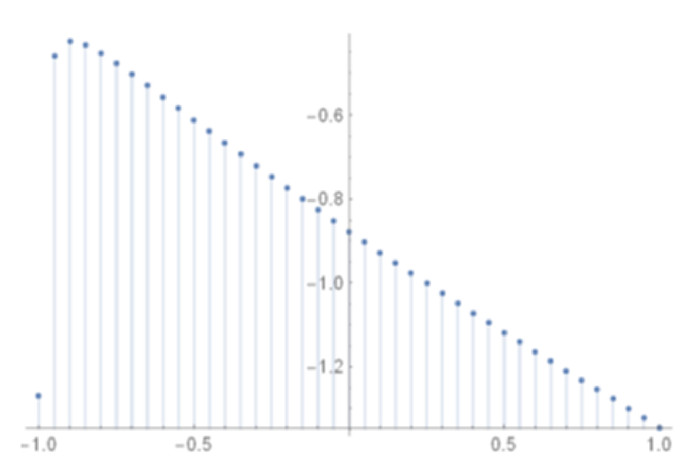
Figure 13.
Image of the function
$ G(A) $ $ A=-1(0.01)(-0.9) $ -
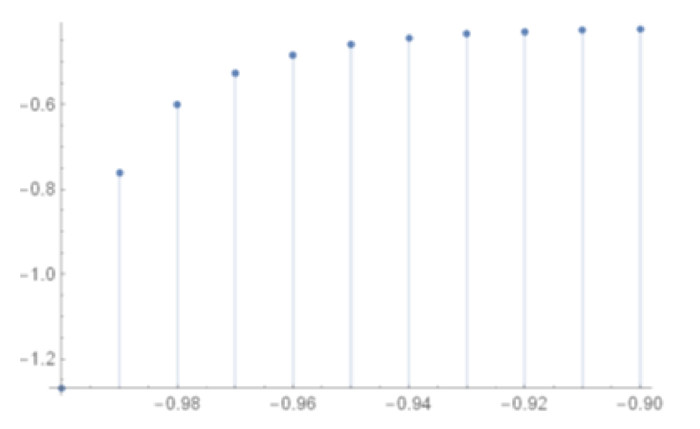
Figure 14.
Plot of empirical distribution function and distribution function for Example 4.1
-
Figure 15.
Plot of empirical distribution function and distribution function for Example 4.2