| Citation: |
Guozhong Xiu, Bao Shi, Liying Wang. INFLUENCE OF INITIAL RAMP ON CONVOLUTIONAL NONVISCOUS DAMPING MATERIALS[J]. Journal of Applied Analysis & Computation, 2023, 13(4): 2343-2353. doi: 10.11948/20220564
|
INFLUENCE OF INITIAL RAMP ON CONVOLUTIONAL NONVISCOUS DAMPING MATERIALS
-
Abstract
In this paper, taking the stress relaxation test of viscoelastic material as an example, the viscoelastic materials used in the test are characterized by the convolutional nonviscous damping model. When the kernel function of the convolutional nonviscous damping model is taken as the power exponential function and the exponential function respectively, the influence of the initial ramp on the stress change is proved theoretically and numerically. This will affect the accuracy of parameter determination of fitting the convolutional nonviscous damping model.
-
-
References
[1] T. Abbasi, F. Faraz and S. Abbas, An alternative precise time integration method for structural systems involving a nonviscous damping model, J. Sound Vib., 2022, 541, 117322. doi: 10.1016/j.jsv.2022.117322 [2] M. Abu-Shady and M. K. A. Kaabar, A generalized definition of the fractional derivative with applications, Mathematical Problems in Engineering, 2021, 2021, 1–9. [3] S. Adhikari, Damping modelling using generalized proportional damping, J. Sound Vib., 2006, 293(1–2), 156–170. doi: 10.1016/j.jsv.2005.09.034 [4] S. Adhikari, Structural dynamic analysis with generalized damping models: analysis, John Wiley & Sons, 2013. [5] S. Adhikari, D. Karličič and X. Liu, Dynamic stiffness of nonlocal damped nano-beams on elastic foundation, J. European Journal of Mechanics-A/Solids, 2021, 86, 104144. [6] W. Chen, Fractional Derivative Modeling in Mechanics and Engineering, New York: Springer, 2022. [7] Z. Ding, L. Zhang and Q. Gao, State-space based discretize-then-differentiate adjoint sensitivity method for transient responses of non-viscously damped systems, J. Computers & Structures, 2021, 250, 106540. [8] M. Di Paola, On the influence of the initial ramp for a correct definition of the parameters of fractional viscoelastic materials, J. Mechanics of Materials, 2014, 69(1), 63–70. doi: 10.1016/j.mechmat.2013.09.017 [9] M. Du, Y. Wang and Z. Wang, Effect of the initial ramps of creep and relaxation tests on models with fractional derivatives, J. Meccanica, 2017, 52(15), 3541–3547. doi: 10.1007/s11012-017-0678-1 [10] X. Du, W. Guo and H. Xia, Dynamic analysis of the non-viscously damped structure using the superposition of first-order ⅡR filters, J. Mech. Syst. Signal. PR., 2022, 167, 108596. doi: 10.1016/j.ymssp.2021.108596 [11] M. Lázaro, Eigensolutions of nonviscously damped systems based on the fixed-point iteration, J. Sound Vib., 2018, 418, 100–121. doi: 10.1016/j.jsv.2017.12.025 [12] M. Lázaro and L. García-Raffi, Boundaries of oscillatory motion in structures with nonviscous dampers, J. Appl. Sci., 2022, 12(5), 2478. doi: 10.3390/app12052478 [13] M. Lázaro and L. García-Raffi, Critical relationships in nonviscous systems with proportional damping, J. Sound Vib., 2020, 485, 115538. doi: 10.1016/j.jsv.2020.115538 [14] L. Li and Y. Hu, Generalized mode acceleration and modal truncation augmentation methods for the harmonic response analysis of nonviscously damped systems, J. Mech. Syst. Signal. PR., 2015, 52, 46–59. [15] L. Li, R. Lin and T. Y. Ng, A fractional nonlocal time-space viscoelasticity theory and its applications in structural dynamics, J. Appl. Math. Model., 2020, 84, 116–136. doi: 10.1016/j.apm.2020.03.048 [16] J. Richter, F. Jin and L. Knipschild, Exponential damping induced by random and realistic perturbations, Physical Review E, 2020, 101(6), 062133. doi: 10.1103/PhysRevE.101.062133 [17] R. Shen, X. Qian and J. Zhou, Characteristics of passive vibration control for exponential non-viscous damping system: Vibration isolator and absorber, J. Vib. Control, 2022, 10775463221130925. [18] R. Shen, X. Qian and J. Zhou, Study on experimental identification and alternative kernel functions of nonviscous damping, International Journal of Applied Mechanics, 2022, 14(8), 2250062. doi: 10.1142/S1758825122500624 [19] W. Shen, C. Zhang and L. Zhang, Stress relaxation behaviour and creep constitutive equations of SA302Gr. C low-alloy steel, J. High Temperature Materials and Processes, 2018, 37(9–10), 857–862. doi: 10.1515/htmp-2017-0090 [20] M. Taneco-Hernández, V. Morales-Delgado and J. Gómez-Aguilar, Fractional KuramotošCSivashinsky equation with power law and stretched Mittag-Leffler kernel, Physica A: Statistical Mechanics and Its Applications, 2019, 527, 121085. doi: 10.1016/j.physa.2019.121085 [21] G. Teodoro and J. Machado, A review of definitions of fractional derivatives and other operators, Journal of Computational Physics, 2019, 388, 195–208. doi: 10.1016/j.jcp.2019.03.008 [22] G. Xiu, B. Shi and F. Qian, Optimal control designs for a class of nonviscously damped systems, Journal of Donghua University, 2020, 37(2), 137–142. [23] G. Xiu, J. Yuan and B. Shi, Hereditary effects of exponentially damped oscillators with past histories, Journal of Applied Analysis & Computation, 2019, 9(6), 2212–2223. -
-
Figures(5)
Export File
Citation
Guozhong Xiu, Bao Shi, Liying Wang. INFLUENCE OF INITIAL RAMP ON CONVOLUTIONAL NONVISCOUS DAMPING MATERIALS[J]. Journal of Applied Analysis & Computation, 2023, 13(4): 2343-2353. doi: 10.11948/20220564
Format
Content
DownLoad:
-
Figure 1.
Real deformation history during the relaxation test.
-
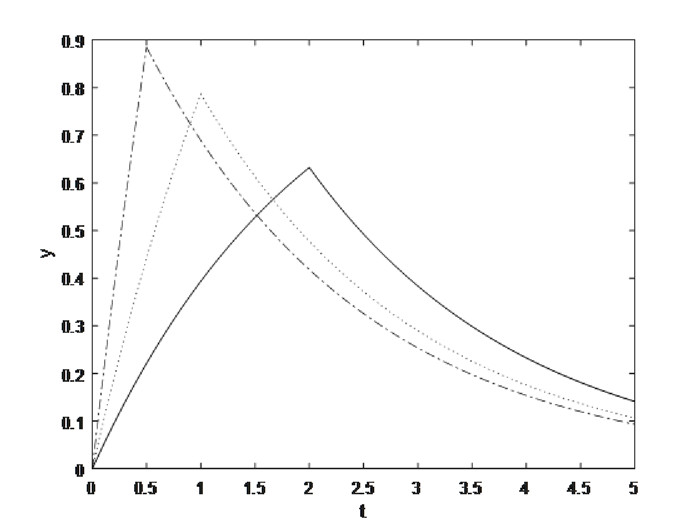
Figure 2.
Change of stress for different value of
$ b_1=0.5 $ $ t_0=0.5,1,2 $ -
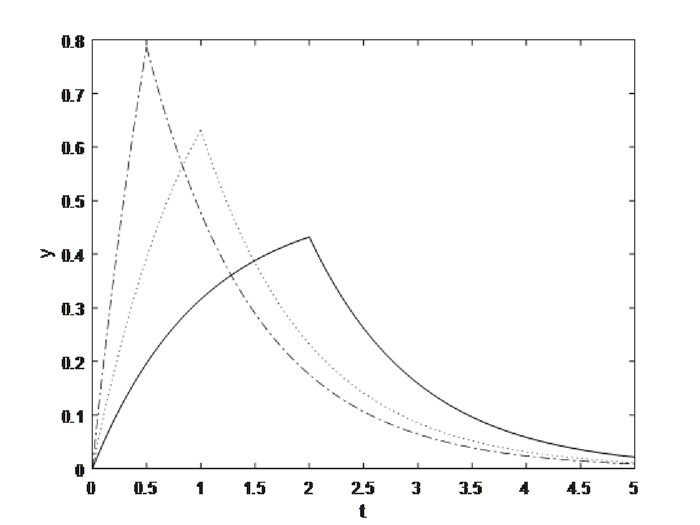
Figure 3.
Change of stress for different value of
$ b_1=1 $ $ t_0=0.5,1,2 $ -
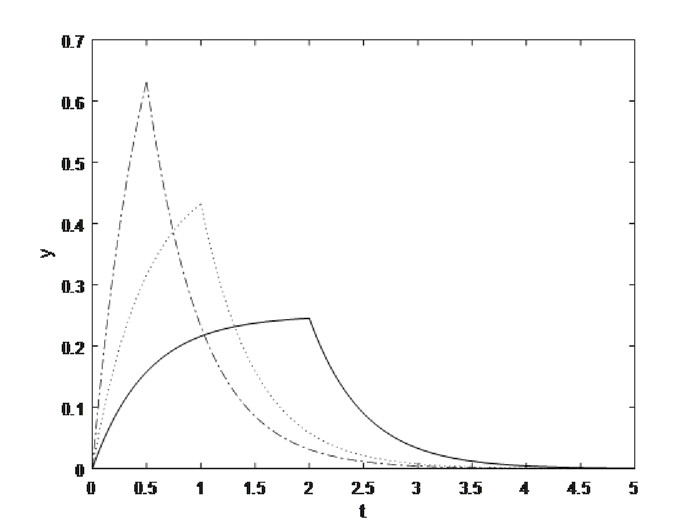
Figure 4.
Change of stress for different value of
$ b_1=2 $ $ t_0=0.5,1,2 $ -
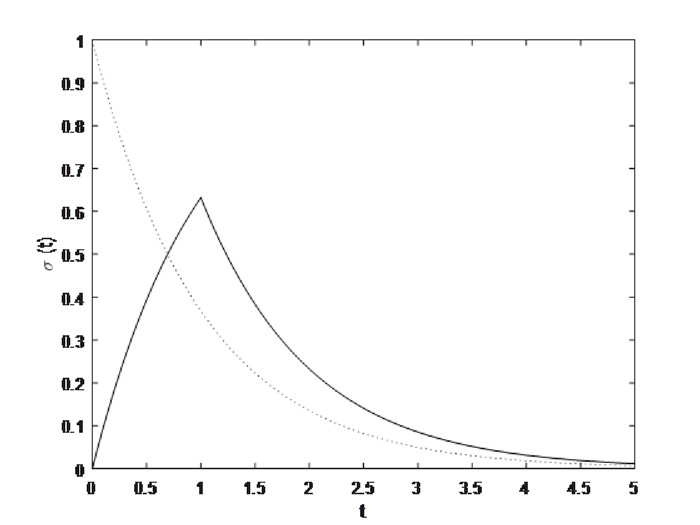
Figure 5.
Influences of initial ramps on relaxation experimental test.