| Citation: |
Gaihui Guo, Feiyan Guo, Bingfang Li, Lixin Yang. THE NON-EXISTENCE AND EXISTENCE OF NON-CONSTANT POSITIVE SOLUTIONS FOR A DIFFUSIVE AUTOCATALYSIS MODEL WITH SATURATION[J]. Journal of Applied Analysis & Computation, 2023, 13(6): 3253-3293. doi: 10.11948/20230002
|
THE NON-EXISTENCE AND EXISTENCE OF NON-CONSTANT POSITIVE SOLUTIONS FOR A DIFFUSIVE AUTOCATALYSIS MODEL WITH SATURATION
-
Abstract
This paper deals with a diffusive autocatalysis model with saturation under Neumann boundary conditions. Firstly, some stability and Turing instability results are obtained. Then by the maximum principle, H$ \ddot{o} $lder inequality and Poincar$ \acute{e} $ inequality, a priori estimates and some basic characterizations of non-constant positive solutions are given. Moreover, some non-existence results are presented for three different situations. In particular, we find that the model does not have any non-constant positive solution when the parameter which represents the saturation rate is large enough. In addition, we use the theories of Leray-Schauder degree and bifurcation to get the existence of non-constant positive solutions, respectively. The steady-state bifurcations at both simple and double eigenvalues are intensively studied and we establish some specific condition to determine the bifurcation direction. Finally, a few of numerical simulations are provided to illustrate theoretical results.
-
-
References
[1] A. Abbad, S. Abdelmalek, S. Bendoukha, et al., A generalized Degn-Harrison reaction-diffusion system: Asymptotic stability and non-existence results, Nonlinear Anal. Real World Appl., 2021, 57, 103191. doi: 10.1016/j.nonrwa.2020.103191 [2] S. Abdelmalek and S. Bendoukha, On the global asymptotic stability of solutions to a generalised Lengyel-Epstein system, Nonlinear Anal. Real World Appl., 2017, 35, 397–413. doi: 10.1016/j.nonrwa.2016.11.007 [3] H. Amann, Fixed point equations and nonlinear eigenvalue problems in ordered Banach spaces, SIAM Rev., 1976, 18, 620–709. doi: 10.1137/1018114 [4] X. Y. Chen and W. H. Jiang, Turing-Hopf bifurcation and multi-stable spatio-temporal patterns in the Lengyel-Epstein system, Nonlinear Anal. Real World Appl., 2019, 49, 386–404. doi: 10.1016/j.nonrwa.2019.03.013 [5] Y. Y. Dong, S. B. Li and S. L. Zhang, Hopf bifurcation in a reaction-diffusion model with Degn-Harrison reaction scheme, Nonlinear Anal. Real World Appl., 2017, 33, 284–297. doi: 10.1016/j.nonrwa.2016.07.002 [6] Z. J. Du, X. N. Zhang and H. P. Zhu, Dynamics of nonconstant steady states of the Sel'kov model with saturation effect, J. Nonlinear Sci., 2020, 30(4), 1553–1577. doi: 10.1007/s00332-020-09617-w [7] R. Engelhardt, Modeling Pattern Formation in Reaction Diffusion Systems, Denmark, Department of Chemistry Laboratory Ⅲ, H. C. Orsted Institute University of Copenhagen, 1994. [8] A. B. Finlayson and J. H. Merkin, Creation of spatial structure by an electric field applied to an ionic cubic autocatalator system, J. Engrg. Math., 2000, 38, 279–296. doi: 10.1023/A:1004799200173 [9] S. M. Fu, X. He, L. N. Zhang, et al., Turing patterns and spatiotemporal patterns in a tritrophic food chain model with diffusion, Nonlinear Anal. Real World Appl., 2021, 59, 103260. doi: 10.1016/j.nonrwa.2020.103260 [10] X. Y. Gao, S. D. Ishag, S. M. Fu, et al., Bifurcation and Turing pattern formation in a diffusive ratio-dependent predator-prey model with predator harvesting, Nonlinear Anal. Real World Appl., 2020, 51, 102962. doi: 10.1016/j.nonrwa.2019.102962 [11] G. H. Guo, B. F. Li, M. H. Wei, et al., Hopf bifurcation and steady-state bifurcation for an autocatalysis reaction-diffusion model, J. Math. Anal. Appl., 2012, 391(1), 265–277. doi: 10.1016/j.jmaa.2012.02.012 [12] G. H. Guo, L. Liu, B. F. Li, et al., Qualitative analysis on positive steady-state solutions for an autocatalysis model with high order, Nonlinear Anal. Real World Appl., 2018, 41, 665–691. doi: 10.1016/j.nonrwa.2017.11.010 [13] G. H. Guo, X. N. Wang, X. L. Lin, et al., Steady-state and Hopf bifurcations in the Langford ODE and PDE systems, Nonlinear Anal. Real World Appl., 2017, 34, 343–362. doi: 10.1016/j.nonrwa.2016.09.008 [14] G. H. Guo, J. H. Wu and X. H. Ren, Hopf bifurcation in general Brusselator system with diffusion, Appl. Math. Mech., 2011, 32(9), 1177–1186. doi: 10.1007/s10483-011-1491-6 [15] A. Hunding and R. Engelhardt, Early biological morphogenesis and nonlinear dynamics, J. Theoret. Biol., 1995, 173, 401–413. doi: 10.1006/jtbi.1995.0072 [16] A. Hunding and P. G. Sorensen, Size adaptation of Turing prepatterns, J. Math. Biol., 1988, 26, 27–39. doi: 10.1007/BF00280170 [17] Y. F. Jia, Y. Li and J. H. Wu, Qualitative analysis on positive steady-states for an autocatalytic reaction model in thermodynamics, Discrete Contin. Dyn. Syst., 2017, 37(9), 4785–4813. doi: 10.3934/dcds.2017206 [18] S. B. Li, J. H. Wu and Y. Y. Dong, Turing patterns in a reaction-diffusion model with the Degn-Harrison reaction scheme, J. Differential Equations, 2015, 259(5), 1990–2029. doi: 10.1016/j.jde.2015.03.017 [19] S. B. Li, J. H. Wu and H. Nie, Steady-state bifurcation and Hopf bifurcation for a diffusive Leslie-Gower predator-prey model, Comput. Math. Appl., 2015, 70(12), 3043–3056. [20] G. M. Lieberman, Bounds for the steady-state Sel'kov model for arbitrary p in any number of dimensions, SIAM J. Math. Anal., 2005, 36(5), 1400–1406. doi: 10.1137/S003614100343651X [21] H. X. Liu, R. C. Wu and B. Liu, Coexistence of activator and inhibitor for Brusselator diffusion system in chemical or biochemical reactions, J. Nonlinear Model. Anal., 2022, 4(3), 539–561. [22] Y. Lou and W. M. Ni, Diffusion, self-diffusion and cross-diffusion, J. Differential Equations, 1996, 131(1), 79–131. doi: 10.1006/jdeq.1996.0157 [23] M. J. Ma and J. J. Hu, Bifurcation and stability analysis of steady states to a Brusselator model, Appl. Math. Comput., 2014, 236, 580–592. [24] D. Mansouri, S. Abdelmalek and S. Bendoukha, Bifurcations and pattern formation in a generalized Lengyel-Epstein reaction-diffusion model, Chaos Solitons Fractals, 2020, 132, 109579. doi: 10.1016/j.chaos.2019.109579 [25] K. Morimoto, Construction of multi-peak solutions to the Gierer-Meinhardt system with saturation and source term, Nonlinear Anal., 2009, 71, 2532–2557. doi: 10.1016/j.na.2009.01.089 [26] J. D. Murray, Mathematical Biology, Springer-Verlag, Berlin, 1993. [27] A. K. M. Nazimuddin, M. Humayun Kabir and M. Osman Gani, Spiral patterns and numerical bifurcation analysis in a three-component Brusselator model for chemical reactions, Math. Comput. Simulation, 2023, 203, 577–591. doi: 10.1016/j.matcom.2022.07.008 [28] Y. Nishiura, Global structure of bifurcating solutions of some reaction-diffusion systems, SIAM J. Math. Anal., 1982, 13(4), 555–593. doi: 10.1137/0513037 [29] R. Peng, J. P. Shi and M. X. Wang, On stationary patterns of a reaction-diffusion model with autocatalysis and saturation law, Nonlinearity, 2008, 21(7), 1471–1488. doi: 10.1088/0951-7715/21/7/006 [30] V. Petrov, S. K. Scott and K. Showalter, Excitability, Wave Reflection, and Wave Splitting in a cubic Autocatalysis Reaction-Diffusion System, Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci., 1994. [31] P. H. Rabinowitz, Some global results for nonlinear eigenvalue problems, J. Funct. Anal., 1971, 7(3), 487–513. doi: 10.1016/0022-1236(71)90030-9 [32] J. P. Shi, Persistence and bifurcation of degenerate solutions, J. Funct. Anal., 1999, 169(2), 494–531. doi: 10.1006/jfan.1999.3483 [33] Q. N. Song, R. Z Yang, C. R. Zhang, et al., Bifurcation analysis of a diffusive perdator-pery model with beddington-deangelis functional response, J. Appl. Anal. Comput., 2021, 11(2), 920–936. [34] J. I. Steinfeld, J. S. Francisco and W. L. Hase, Chemical Kinetics and Dynamics, Prentice-Hall, 1999. [35] I. Takagi, Point-condensation for a reaction-diffusion system, J. Differential Equations, 1986, 61(2), 208–249. doi: 10.1016/0022-0396(86)90119-1 [36] P. Wang and Y. B. Gao, Turing instability of the periodic solutions for the diffusive Sel'kov model with saturation effect, Nonlinear Anal. Real World Appl., 2022, 63, 103417. doi: 10.1016/j.nonrwa.2021.103417 [37] X. P. Yan, J. Y. Chen and C. H. Zhang, Dynamics analysis of a chemical reaction-diffusion model subject to Degn-Harrison reaction scheme, Nonlinear Anal. Real World Appl., 2019, 48, 161–181. doi: 10.1016/j.nonrwa.2019.01.005 [38] X. Yan, Y. L. Li and G. H. Guo, Qualitative analysis on a diffusive predator-prey model with toxins, J. Math. Anal. Appl., 2020, 486(10), 123868. [39] X. P. Yan and C. H. Zhang, Turing instability and formation of temporal patterns in a diffusive bimolecular model with saturation law, Nonlinear Anal. Real World Appl., 2018, 43, 54–77. doi: 10.1016/j.nonrwa.2018.02.004 [40] W. B. Yang, Z. Y. Wei, H. L. Jianget, et al., The existence of steady states for a bimolecular model with autocatalysis and saturation law, Z. Angew. Math. Phys., 2018, 69(5), 131. doi: 10.1007/s00033-018-1024-8 [41] F. Q. Yi, Turing instability of the periodic solutions for reaction-diffusion systems with cross-diffusion and the patch model with cross-diffusion-like coupling, J. Differential Equations, 2021, 281(25), 379–410. [42] F. Q. Yi, J. X. Liu and J. J. Wei, Spatiotemporal pattern formation and multiple bifurcations in a diffusive bimolecular model, Nonlinear Anal. Real World Appl., 2010, 11(5), 3770–3781. doi: 10.1016/j.nonrwa.2010.02.007 [43] F. Q. Yi, J. J. Wei and J. P. Shi, Diffusion-driven instability and bifurcation in the Lengyel-Epstein system, Nonlinear Anal. Real World Appl., 2008, 9(3), 1038–1051. doi: 10.1016/j.nonrwa.2007.02.005 [44] L. Zhang and S. Y. Liu, Stability and pattern formation in a coupled arbitrary order of autocatalysis system, Appl. Math. Model., 2009, 33(2), 884–896. doi: 10.1016/j.apm.2007.12.013 [45] J. T. Zhao and Y. F. Jia, Stability analysis on steady-state bifurcation for arbitrary order autocatalytic reaction model, Appl. Math. Lett., 2019, 95, 98–103. doi: 10.1016/j.aml.2019.03.027 [46] J. Zhou and J. P. Shi, Pattern formation in a genernal glycolysis reaction-diffusion system, IMA J. Appl. Math., 2015, 80(6), 1703–1738. doi: 10.1093/imamat/hxv013 -
-
Figures(11)
Export File
Citation
Gaihui Guo, Feiyan Guo, Bingfang Li, Lixin Yang. THE NON-EXISTENCE AND EXISTENCE OF NON-CONSTANT POSITIVE SOLUTIONS FOR A DIFFUSIVE AUTOCATALYSIS MODEL WITH SATURATION[J]. Journal of Applied Analysis & Computation, 2023, 13(6): 3253-3293. doi: 10.11948/20230002
Format
Content
DownLoad:
-
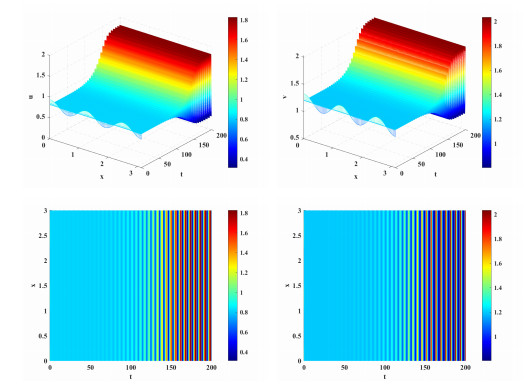
Figure 1.
The equilibrium
$ E^* $ $ a=0.9, p=2, k=0.8, d_1=0.5, d_2=1 $ -
Figure 2.
Positive periodic solution of (1.2) for
$ a=0.9, p=2, k=0.23, d_1=0.5, d_2=1 $ -
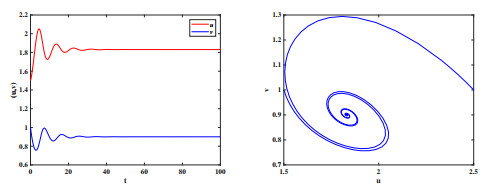
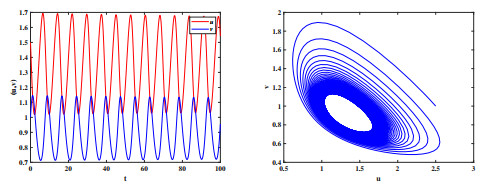
Figure 3.
The trajectory graph (left) and phase portrait (right) of (1.2) for
$ a=0.9, p=2, k=0.8, d_1=0.5, d_2=1 $ -
Figure 4.
The trajectory graph (left) and phase portrait (right) of (1.2) for
$ a=0.9, p=2, k=0.23, d_1=0.5, d_2=1 $ -
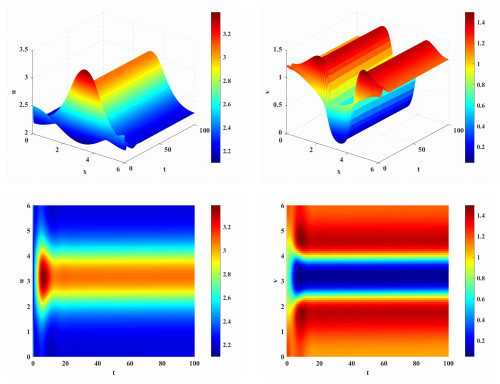
Figure 5.
The equilibrium
$ E^* $ $ a=1, p=4, k=2, d_1=1, d_2=0.05 $ -
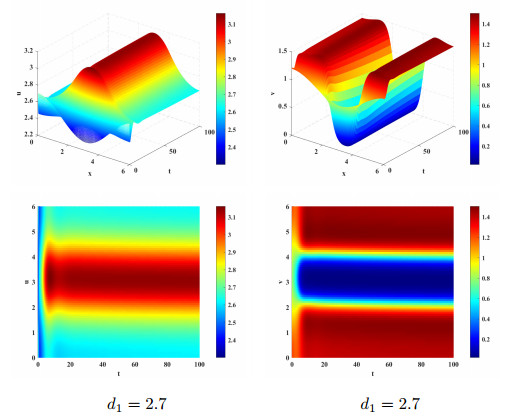
Figure 6.
Steady-state bifurcation solution at the simple eigenvalue of (1.3) for
$ a=1, p=3, k=1.5, d_2=0.045. $ $ d_{1}=2.7 $ -
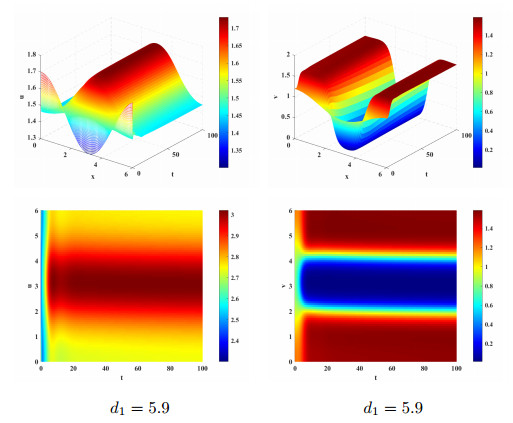
Figure 7.
Steady-state bifurcation solution at the simple eigenvalue for
$ a=1, p=3, k=1.5, d_2=0.045 $ $ d_1=5.9 $ -
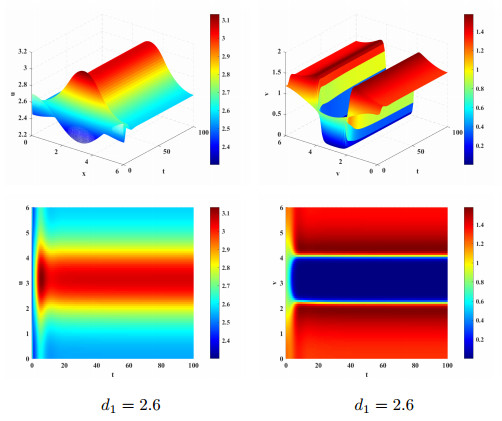
Figure 8.
Steady-state bifurcation solution at the double eigenvalue for
$ a=1, p=3, k=1.5, d_2=0.039 $ $ d_1=2.6 $ -
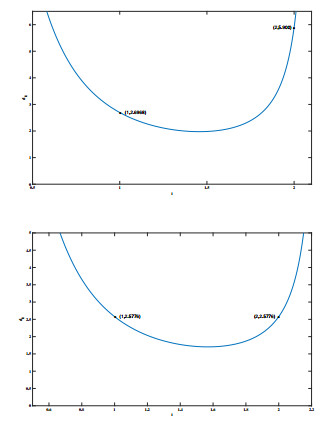
Figure 9.
The neutral curves
$ d_1 $ $ i\in \mathbb{N} $ $ a=1, p=3, k=1.5 $ $ d_2=0.045 $ $ d_2=0.039 $ -
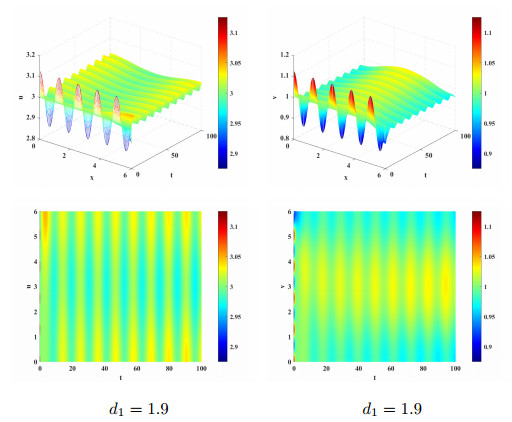
Figure 10.
Positive periodic solution of (1.2) for
$ a=1, p=4, k=2, d_2=0.14 $ $ d_1=1.9 $ -
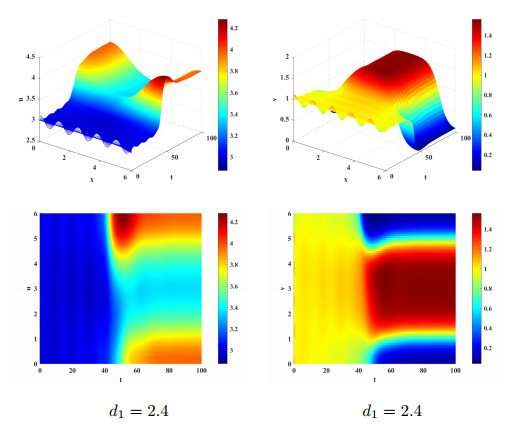
Figure 11.
Positive periodic solution shifts to the steady-state for
$ a=1, p=4, k=2, d_2=0.14 $ $ d_1=2.4 $