| Citation: | Ziqiang Wang, Qing Tan, Zhongqing Wang, Junying Cao. MULTIQUADRIC QUASI-INTERPOLATION METHOD FOR FRACTIONAL INTEGRAL-DIFFERENTIAL EQUATIONS[J]. Journal of Applied Analysis & Computation, 2024, 14(5): 2534-2557. doi: 10.11948/20230011 |
MULTIQUADRIC QUASI-INTERPOLATION METHOD FOR FRACTIONAL INTEGRAL-DIFFERENTIAL EQUATIONS
-
Abstract
In this paper, Multiquadric quasi-interpolation method is used to approximate fractional integral equations and fractional differential equations. Firstly, we construct two operators for approximating the Hadamard integral-differential equation based on quasi interpolators, and verify their properties and order of convergence. Secondly, we obtain that the approximation order of the numerical integral scheme is 3, and the approximation order of the numerical scheme is 3-μ for μ(0 < μ < 1) order fractional Hadamard derivative. Finally, the results of numerical experiments show that the numerical results are in agreement with the theoretical analysis.
-

-
References
[1] J. Cao and C. Xu, A high order schema for the numerical solution of the fractional ordinary differential equations, J. Comput. Phys., 2013, 238, 154–168. doi: 10.1016/j.jcp.2012.12.013 [2] D. Cen, C. Ou and Z. Wang, Efficient numerical algorithms of time fractional telegraph-type equations involving Hadamard derivatives, Math. Methods Appl. Sci., 2022, 45(12), 7576–7590. doi: 10.1002/mma.8263 [3] R. Chen and Z. Wu, Solving partial differential equation by using multiquadric quasi-interpolation, Appl. Math. Comput., 2007, 186(2), 1502–1510. [4] E. Fan, C. Li and Z. Li, Numerical approaches to Caputo-Hadamard fractional derivatives with applications to long-term integration of fractional differential systems, Commun. Nonlinear Sci. Numer. Simul., 2022. DOI: 10.1016/j.cnsns.2021.106096. [5] S. Fazlollah and S. Zhu, Error and stability estimates of a time-fractional option pricing model under fully spatial-temporal graded meshes, J. Comput. Appl. Math., 2023. DOI: 10.1016/j.cam.2023.115075. [6] R. Feng and J. Duan, High accurate finite differences based on RBF Interpolation and its application in solving differential equations, J. Sci. Comput., 2018, 76, 1785–1812. doi: 10.1007/s10915-018-0684-z [7] R. Feng and F. Li, A shape-preserving quasi-interpolation operator satisfying quadratic polynomial reproduction property to scattered data, J. Comput. Appl. Math., 2009, 225(2), 594–601. doi: 10.1016/j.cam.2008.08.024 [8] W. Gao, J. Wang and R. Zhang, Quasi-interpolation for multivariate density estimation on bounded domain, Math. Comput. Simulation, 2023, 203, 592–608. doi: 10.1016/j.matcom.2022.07.006 [9] W. Gao, X. Zhang and X. Zhou, Multiquadric quasi-interpolation for integral functionals, Math. Comput. Simulation, 2020, 177, 316–328. doi: 10.1016/j.matcom.2020.04.015 [10] R. Ghaffari and F. Ghoreishi, Error analysis of the reduced RBF model based on POD method for time-fractional partial differential equations, Acta Appl. Math., 2020, 168(1), 33–55. doi: 10.1007/s10440-019-00278-w [11] M. Hussain, S. Haq and A. Ghafoor, Meshless spectral method for solution of time-fractional coupled KdV equations, Appl. Math. Comput., 2019, 341, 321–334. [12] M. Jabalameli and D. Mirzaei, A weak-form RBF-generated finite difference method, Computers and Mathematics with Applications, 2020, 79(9), 2624–2643. doi: 10.1016/j.camwa.2019.11.024 [13] F. Jarad, T. Abdeljawad and D. Baleanu, Caputo-type modification of the Hadamard fractional derivatives, Adv. Difference Equ., 2012. DOI: 10.1186/1687-1847-2012-142. [14] M. Li, Y. Wang and L. Ling, Numerical caputo differentiation by radial basis functions, J. Sci. Comput., 2015, 62, 300–315. doi: 10.1007/s10915-014-9857-6 [15] H. Liang and H. Brunner, The fine error estimation of collocation methods on uniform meshes for weakly singular volterra integral equations, J. Sci. Comput., 2020. DOI: 10.1007/s10915-020-01266-1. [16] H. Liang and H. Brunner, The convergence of collocation solutions in continuous piecewise polynomial spaces for weakly singular volterra integral equations, SIAM J. Numer. Anal., 2019, 57(4), 1875–1896. doi: 10.1137/19M1245062 [17] J. Liu, X. Li and X. Hua, A RBF-based differential quadrature method for solving two-dimensional variable-order time fractional advection-diffusion equation, J. Comput. Phys., 2019, 384, 222–238. doi: 10.1016/j.jcp.2018.12.043 [18] H. Pourbashash and M. Oshagh, Local RBF-FD technique for solving the two-dimensional modified anomalous sub-diffusion equation, Appl. Math. Comput., 2018, 339, 144–152. [19] Y. Qiao, J. Zhao and X. Feng, A compact integrated RBF method for time fractional convection-diffusion-reaction equations, Comput. Math. Appl., 2019, 77(9), 2263–2278. doi: 10.1016/j.camwa.2018.12.017 [20] N. Sharon, R. Cohen and H. Wendland, On multiscale quasi-interpolation of scattered scalar-and manifold-valued functions, SIAM J. Sci. Comput., 2023, 45, A2458–A2482. doi: 10.1137/22M1528306 [21] F. Soleymani and S. Zhu, RBF-FD solution for a financial partial-integro differential equation utilizing the generalized multiquadric function, Comput. Math. Appl., 2021, 82, 161–178. doi: 10.1016/j.camwa.2020.11.010 [22] Z. Sun and Y. Gao, High order multiquadric trigonometric quasi-interpolation method for solving time-dependent partial differential equations, Numer. Algorithms, 2023, 93(4), 1719–1739. doi: 10.1007/s11075-022-01486-6 [23] V. Uchaikin, Fractional Derivatives for Physicists and Engineers, Berlin: Springer, 2013. [24] Z. Wang and J. Cao, Multiquadric quasi-interpolation method for fractional diffusion equations in space (in Chinese), J. Xiamen Univ., 2015, 54(3), 358–363. [25] Q. Xu and Z. Zheng, Spectral collocation method for fractional differential/integral equations with generalized fractional operator, Int. J. Differ. Equ. Appl., 2019. DOI: 10.1155/2019/3734617. [26] F. Zafarghandi and M. Mohammadi, Numerical approximations for the riesz space fractional advection-dispersion equations via radial basis functions, Appl. Numer. Math., 2019, 144, 59–82. doi: 10.1016/j.apnum.2019.05.011 [27] F. Zafarghandi, M. Mohammadi and E. Babolian, Radial basis functions method for solving the fractional diffusion equations, Appl. Math. Comput., 2019, 342, 224–246. -
-
-
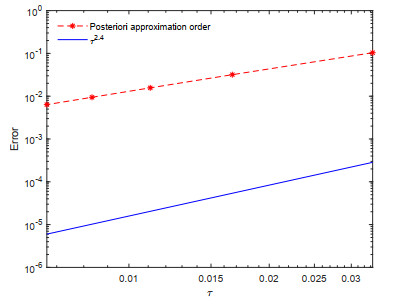
Figure 1.
Log-log sketches of approximation orders with µ = 0.3 for Example 4.5.
-
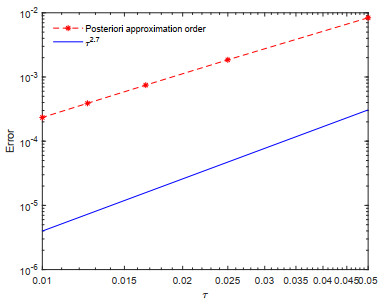
Figure 2.
Log-log sketches of approximation orders with µ = 0.6 for Example 4.5.




 DownLoad:
DownLoad: