| Citation: |
Shan Jiang, Xiao Ding, Meiling Sun. PARAMETER-UNIFORM SUPERCONVERGENCE OF MULTISCALE COMPUTATION FOR SINGULAR PERTURBATION EXHIBITING TWIN BOUNDARY LAYERS[J]. Journal of Applied Analysis & Computation, 2023, 13(6): 3330-3351. doi: 10.11948/20230020
|
PARAMETER-UNIFORM SUPERCONVERGENCE OF MULTISCALE COMPUTATION FOR SINGULAR PERTURBATION EXHIBITING TWIN BOUNDARY LAYERS
-
Abstract
We propose a multiscale finite element scheme on a graded mesh for solving a singularly perturbed convection-diffusion problem efficiently. Twin boundary layers phenomena are shown in the one-dimensional model, and an adaptively graded mesh is applied to probe the twin boundary jumps. We evoke an updated multiscale strategy through the multiscale basis functions in a linear Lagrange style. Detailed mapping behaviors are investigated on fine as well as on coarse scales, thus incorporating information at the micro-scale into the macroscopic data. High-order stability theorems in an energy norm of multiscale errors are addressed. Our approach can achieve a parameter-uniform superconvergence with limited computational costs on the coarse graded mesh. Numerical results support the high-order convergence theorem and validate the advantages over other prevalent methods in the literature, especially for the singular perturbation with very small parameters. The proposed method is twin boundary layers resolving as well as parameter uniform superconvergent.
-
-
References
[1] M. Brdar, G. Radojev, H. G. Roos and L. Teofanov, Superconvergence analysis of FEM and SDFEM on graded meshes for a problem with characteristic layers, Comput. Math. Appl., 2021, 93, 50–57. [2] M. Brdar and H. Zarin, A singularly perturbed problem with two parameters on a Bakhvalov-type mesh, J. Comput. Appl. Math., 2016, 292, 307–319. doi: 10.1016/j.cam.2015.07.011 [3] M. Brdar, H. Zarin and L. Teofanov, A singularly perturbed problem with two parameters in two dimensions on graded meshes, Comput. Math. Appl., 2016, 72, 2582–2603. [4] D. F. Cai, Z. Q. Cai and S. Zhang, Robust equilibrated a posteriori error estimator for higher order finite element approximations to diffusion problems, Numer. Math., 2020, 144, 1–21. doi: 10.1007/s00211-019-01075-1 [5] Z. D. Cen, A. M. Xu and A. B. Le, A high-order finite difference scheme for a singularly perturbed fourth-order ordinary differential equation, Inter. J. Comput. Math., 2018, 95(9), 1–14. [6] Y. Cheng, On the local discontinuous Galerkin method for singularly perturbed problem with two parameters, J. Comput. Appl. Math., 2021, 392, 113485. doi: 10.1016/j.cam.2021.113485 [7] Y. Cheng, S. Jiang and M. Stynes, Supercloseness of the local discontinuous Galerkin method for a singularly perturbed convection-diffusion problem, Math. Comput., 2023, 92(343), 2065–2095. doi: 10.1090/mcom/3844 [8] Y. Cheng, Y. J. Mei and H. G. Roos, The local discontinuous Galerkin method on layer-adapted meshes for time-dependent singularly perturbed convection-diffusion problems, Comput. Math. Appl., 2022, 117, 245–256. [9] E. Chung and Y. B. Li, Adaptive generalized multiscale finite element methods for H(curl)-elliptic problems with heterogeneous coefficients, J. Computat. Appl. Math., 2019, 345, 357–373. doi: 10.1016/j.cam.2018.06.052 [10] P. Constantinou, S. Franz, L. Ludwig and C. Xenophontos, Finite element approximation of reaction-diffusion problems using an exponentially graded mesh, Comput. Math. Appl., 2018, 76, 2523–2534. [11] R. G. Dur$\acute{a}$n and A. L. Lombardi, Finite element approximation of convection diffusion problems using graded meshes, Appl. Numer. Math., 2006, 56, 1314–1325. doi: 10.1016/j.apnum.2006.03.029 [12] E. G. M. Elmahdi and J. F. Huang, Efficient numerical solution of two-dimensional time-space fractional nonlinear diffusion-wave equations with initial singularity, J. Appl. Anal. Comput., 2022, 12(2), 831–849. [13] F. Z. Geng and S. P. Qian, Reproducing kernel method for singularly perturbed turning point problems having twin boundary layers, Appl. Math. Letters, 2013, 26, 998–1004. doi: 10.1016/j.aml.2013.05.006 [14] L. Govindarao and J. Mohapatra, A numerical scheme to solve mixed parabolic-elliptic problem involving singular perturbation, Inter. J. Comput. Math, 2022, 99(10), 2069–2090. doi: 10.1080/00207160.2022.2037131 [15] V. Gupta, M. K. Kadalbajoo and R. K. Dubey, A parameter-uniform higher order finite difference scheme for singularly perturbed time-dependent parabolic problem with two small parameters, Inter. J. Comput. Math., 2019, 96(3), 474–499. doi: 10.1080/00207160.2018.1432856 [16] S. Jiang, L. Liang, M. L. Sun and F. Su, Uniform high-order convergence of multiscale finite element computation on a graded recursion for singular perturbation, Electr. Research Archive, 2020, 28(2), 935–949. doi: 10.3934/era.2020049 [17] S. Jiang, M. Presho and Y. Q. Huang, An adapted Petrov-Galerkin multiscale finite element for singularly perturbed reaction-diffusion problems, Inter. J. Comput. Math., 2016, 93(7), 1200–1211. doi: 10.1080/00207160.2015.1041935 [18] S. Jiang, M. L. Sun and Y. Yang, Reduced multiscale computation on adapted grid for the convection-diffusion Robin problem, J. Appl. Anal. Comput., 2017, 7(4), 1488–1502. [19] M. K. Kadalbajoo, P. Arora and V. Gupta, Collocation method using artificial viscosity for solving stiff singularly perturbed turning point problem having twin boundary layers, Comput. Math. Appl., 2011, 61, 1595–1607. [20] M. K. Kadalbajoo and V. Gupta, A parameter uniform B-spline collocation method for solving singularly perturbed turning point problem having twin boundary layers, Inter. J. Comput. Math., 2010, 87(14), 3218–3235. doi: 10.1080/00207160902980492 [21] M. K. Kadalbajoo and K. C. Patidar, Variable mesh spline approximation method for solving singularly perturbed turning point problems having boundary layer(s), Comput. Math. Appl., 2001, 42, 1439–1453. [22] A. Kaushik, A. K. Vashishth, V. Kumar and M. Sharma, A modified graded mesh and higher order finite element approximation for singular perturbation problems, J. Comput. Physics, 2019, 395, 275–285. doi: 10.1016/j.jcp.2019.04.073 [23] D. Kumar, A parameter-uniform method for singularly perturbed turning point problems exhibiting interior or twin boundary layers, Inter. J. Comput. Math., 2019, 96(5), 865–882. doi: 10.1080/00207160.2018.1458098 [24] T. Linb, Layer-adapted meshes for convection-diffusion problems, Comput. Method. Appl. Mech. Engin., 2003, 192, 1061–1105. doi: 10.1016/S0045-7825(02)00630-8 [25] X. W. Liu and J. Zhang, Galerkin finite element methods for convection-diffusion problems with exponential layers on Shishkin triangular meshes and hybrid meshes, Appl. Math. Comput., 2017, 307, 244–256. [26] R. K. Lodhi and H. K. Mishra, Quintic B-spline method for solving second order linear and nonlinear singularly perturbed two-point boundary value problems, J. Comput. Appl. Math., 2017, 319, 170–187. doi: 10.1016/j.cam.2017.01.011 [27] S. Natesan, J. Jayakumar and J. Vigo-Aguiar, Parameter-uniform numerical method for singularly perturbed turning point problems exhibiting boundary layers, J. Comput. Appl. Math., 2003, 158, 121–134. doi: 10.1016/S0377-0427(03)00476-X [28] E. Oriordan, M. L. Pickett and G. I. Shishkin, Parameter-uniform finite difference schemes for singularly perturbed parabolic diffusion-convection-reaction problems, Math. Comput., 2006, 75, 1135–1154. doi: 10.1090/S0025-5718-06-01846-1 [29] H. G. Roos, L. Teofanov and Z. Uzelac, A modified Bakhvalov mesh, Appl. Math. Letters, 2014, 31, 7–11. doi: 10.1016/j.aml.2014.01.001 [30] H. G. Roos, L. Teofanov and Z. Uzelac, Graded meshes for higher order FEM, J. Comput. Math., 2015, 33, 1–16. doi: 10.4208/jcm.1405-m4362 [31] K. K. Sharma, P. Rai and K. C. Patidar, A review on singularly perturbed differential equations with turning points and interior layers, Appl. Math. Comput., 2013, 219, 10575–10609. [32] Q. Yang and M. K. Ni, Asymptotics of a class of singularly perturbed weak nonlinear boundary value problem with a multiple root of the degenerate equation, J. Nonlinear Model. Anal., 2022, 4(3), 502–513. [33] Y. H. Yin and P. Zhu, The streamline-diffusion finite element method on graded meshes for a convection-diffusion problem, Appl. Numer. Math., 2019, 138, 19–29. doi: 10.1016/j.apnum.2018.12.012 -
-
Figures(6) / Tables(3)
Export File
Citation
Shan Jiang, Xiao Ding, Meiling Sun. PARAMETER-UNIFORM SUPERCONVERGENCE OF MULTISCALE COMPUTATION FOR SINGULAR PERTURBATION EXHIBITING TWIN BOUNDARY LAYERS[J]. Journal of Applied Analysis & Computation, 2023, 13(6): 3330-3351. doi: 10.11948/20230020
Format
Content
DownLoad:
-
Figure 1.
For
$ N=4 $ $ M=2 $ $ N+1=5 $ $ N*M+1=9 $ -
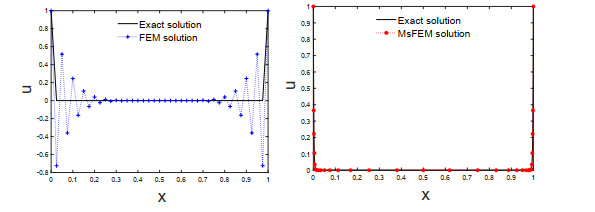
Figure 2.
Exact and FEM solution on uniform mesh
$ N=40 $ $ N=30 $ $ \varepsilon=2^{-8} $ -
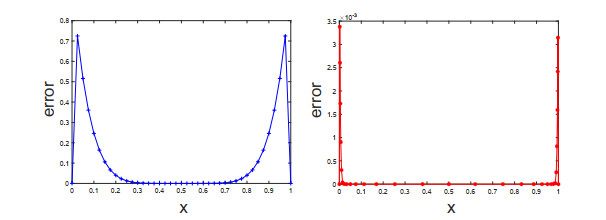
Figure 3.
Errors of FEM(U) on
$ N=40 $ $ N=30 $ $ \varepsilon=2^{-8} $ -
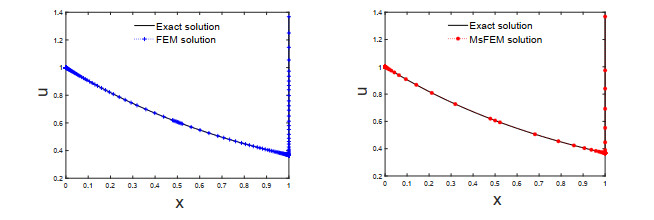
Figure 4.
Exact and FEM solution on fine graded mesh
$ N=424 $ $ N=106 $ $ \varepsilon=10^{-9} $ -
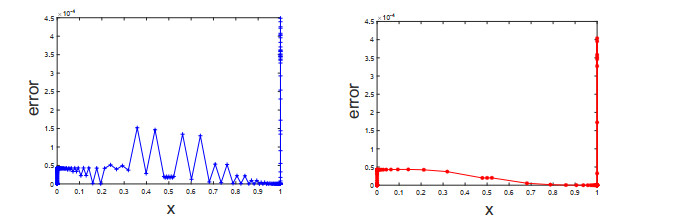
Figure 5.
Errors of FEM(G) on fine mesh
$ N=424 $ $ N=106 $ $ \varepsilon=10^{-9} $ -
Figure 6.
Convergence history for
$ Err_{\infty} $ $ Err_{en} $ $ \varepsilon=10^{-8} $ $ 10^{-10} $