| Citation: | M. Pourbabaee, A. Saadatmandi. NEW OPERATIONAL MATRIX OF RIEMANN-LIOUVILLE FRACTIONAL DERIVATIVE OF ORTHONORMAL BERNOULLI POLYNOMIALS FOR THE NUMERICAL SOLUTION OF SOME DISTRIBUTED-ORDER TIME-FRACTIONAL PARTIAL DIFFERENTIAL EQUATIONS[J]. Journal of Applied Analysis & Computation, 2023, 13(6): 3352-3373. doi: 10.11948/20230039 |
NEW OPERATIONAL MATRIX OF RIEMANN-LIOUVILLE FRACTIONAL DERIVATIVE OF ORTHONORMAL BERNOULLI POLYNOMIALS FOR THE NUMERICAL SOLUTION OF SOME DISTRIBUTED-ORDER TIME-FRACTIONAL PARTIAL DIFFERENTIAL EQUATIONS
-
Abstract
In this article, the orthonormal Bernoulli polynomials (OBPs) and their properties are applied for concluding a general technique for forming a new operational matrix of the distributed-order (DO) fractional derivative. Then, we apply tau approach and obtained operational matrix to solve some DO time-fractional partial differential equations including distributed-order Rayleigh-Stokes problem (DRSP) for a generalized second-grade fluid and DO anomalous sub-diffusion equation. Our methodology reduces the solution of these problems to a set of algebraic equations. By analysis the error of approximation by the obtained matrix and comparing between the numerical solutions and exact result, we can conclude that this operational matrix is valid to solve the mentioned equations. Also, to confirm the accuracy and the validity of our technique three examples are provided. Finally, we compare obtained results from this approach with the achieved results from relevant studies.
-

-
References
[1] M. Abbaszadeh and M. Dehghan, An improved meshless method for solving two-dimensional distributed-order time fractional diffusion-wave equation with error estimate, Numer. Algor., 2017, 75, 173–211. doi: 10.1007/s11075-016-0201-0 [2] M. Abbaszadeh and M. Dehghan, Numerical investigation of reproducing kernel particle Galerkin method for solving fractional modified distributed-order anomalous sub-diffusion equation with error estimation, Appl. Math. Comput., 2021, 392, 125718. [3] M. A. Abdelkawy and R. T. Alqahtani, Shifted Jacobi collocation method for solving multi-dimensional fractional Stokes' first problem for a heated generalized second grade fluid, Adv. Difference Equ., 2016, 114, 17pp. [4] A. A. Alikhanov, Numerical methods of solutions of boundary value problems for the multi-term variable-distributed-order diffusion equation, Appl. Math. Comput., 2015, 268, 12–22. [5] S. Bazm, Bernoulli polynomials for the numerical solution of some classes of linear and nonlinear integral equations, J. Comput. Appl. Math., 2015, 275, 44–60. doi: 10.1016/j.cam.2014.07.018 [6] A. H. Bhrawy, M. A. Zaky and J. F. Alzaidy, Two shifted Jacobi-Gauss collocation schemes for solving two-dimensional variable-order fractional Rayleigh-Stokes problem, Adv. Difference Equ., 2016, 272, 17pp. [7] W. Bu, A. Xiao and W. Zeng, Finite difference/finite element methods for distributed-order time fractional diffusion equations, J. Sci. Comput., 2017, 72, 422–441. doi: 10.1007/s10915-017-0360-8 [8] M. Caputo, Linear models of dissipation whose q is almost frequency independent -ii, Geophys J. R. Astr. Soc., 1967, 13, 529–539. doi: 10.1111/j.1365-246X.1967.tb02303.x [9] Y. Chen and C. M. Chen, Numerical algorithm for solving the Stokes' first problem for a heated generalized second grade fluid with fractional derivative, Numer. Algorithms, 2018, 77, 939–953. doi: 10.1007/s11075-017-0348-3 [10] H. Dehestani, Y. Ordokhani and M. Razzaghi, Fractional-order Legendre-Laguerre functions and their applications in fractional partial differential equations, Appl. Math. Comput., 2018, 336, 433–453. [11] M. Dehghan and M. Abbaszadeh, A finite element method for the numerical solution of Rayleigh-Stokes problem for a heated generalized second grade fluid with fractional derivatives, Eng. Comput., 2017, 33, 587–605. doi: 10.1007/s00366-016-0491-9 [12] K. Diethelm and N. J. Ford, Numerical analysis for distributed-order differential equations, J. Comput. Appl. Math., 2009, 225, 96–104. doi: 10.1016/j.cam.2008.07.018 [13] W. Fan and F. Liu, A numerical method for solving the two-dimensional distributed-order space-fractional diffusion equation on an irregular convex domain, Appl. Math. Lett., 2018, 77, 114–121. doi: 10.1016/j.aml.2017.10.005 [14] G. Fernández-Anaya, G. Nava-Antonio, J. Jamous-Galante, R. Muñoz-Vega and E. G. Hernández-Martinez, Asymptotic stability of distributed-order nonlinear dynamical systems, Commun. Nonlinear Sci. Numer. Simul., 2017, 48, 541–549. doi: 10.1016/j.cnsns.2017.01.020 [15] N. J. Ford, M. L. Morgado and M. Rebelo, An implicit finite difference approximation for the solution of the diffusion equation with distributed-order in time, Electron. Trans. Numer. Anal., 2015, 44, 289–305. [16] G. Gao, A. A. Alikhanov and Z. Sun, The temporal second order difference schemes based on the interpolation approximation for solving the time multi-term and distributed-order fractional sub-diffusion equations, J. Sci. Comput., 2017, 73, 93–121. doi: 10.1007/s10915-017-0407-x [17] G. H. Gao, H. W. Sun and Z. Z. Sun, Some high-order difference schemes for the distributed-order differential equations, J. Comput. Phys., 2015, 298, 337–359. doi: 10.1016/j.jcp.2015.05.047 [18] G. H. Gao and Z. Z. Sun, Two alternating direction implicit difference schemes with the extrapolation method for the two-dimensional distributed-order differential equations, Comput. Math. Appl., 2015, 69, 926–948. [19] A. Golbabai and S. Panjeh Ali Beik, An efficient method based on operational matrices of Bernoulli polynomials for solving matrix differential equations, Comput. Appl. Math., 2015, 34, 159–175. doi: 10.1007/s40314-013-0110-y [20] R. M. Hafez, M. A. Zaky and M. A. Abdelkawy, Jacobi spectral galerkin method for distributed-order fractional Rayleigh-Stokes problem for a generalized second grade fluid, Front. Phys., 2020, 7, 1–10. [21] A. Haghbin and H. Jafari, Solving time-fractional chemical engineering equations by modified variational iteration method as fixed point iteration method, Iranian J. Math. Chem., 2017, 8, 365–375. [22] M. H. Heydari and Z. Avazzadeh, New formulation of the orthonormal Bernoulli polynomials for solving the variable-order time fractional coupled Boussinesq-Burger's equations, Eng Comput., 2021, 37, 3509–3517. doi: 10.1007/s00366-020-01007-w [23] M. H. Heydari, M. Hosseininia and D. Baleanu, A computational approach based on the fractional Euler functions and Chebyshev cardinal functions for distributed-order time fractional 2D diffusion equation, Alex. Eng. J., 2023, 67, 643–653. doi: 10.1016/j.aej.2022.12.065 [24] M. H. Heydari, S. Rashid and Y. -M. Chu, Chelyshkov polynomials method for distributed-order time fractional nonlinear diffusion-wave equations, Results Phys., 2023, 47, 106344. doi: 10.1016/j.rinp.2023.106344 [25] M. H. Heydari, S. Rashid and F. Jarad, A numerical method for distributed-order time fractional 2D Sobolev equation, Results Phys., 2023, 45, 106211. doi: 10.1016/j.rinp.2023.106211 [26] M. H. Heydari, M. Razzaghi and D. Baleanu, Numerical solution of distributed-order time fractional Klein–Gordon–Zakharov system, J. Comput. Sci., 2023, 67, 101961. doi: 10.1016/j.jocs.2023.101961 [27] M. H. Heydari, M. Razzaghi and D. Baleanu, A numerical method based on the piecewise Jacobi functions for distributed-order fractional Schrödinger equation, Commun. Nonlinear Sci. Numer. Simul., 2023, 116, 106873. doi: 10.1016/j.cnsns.2022.106873 [28] F. B. Hildebrand, Introduction to Numerical Analysis, Dover Publications, New York, 1956. [29] Z. Jiao, Y. Chen and I. Podlubny, Distributed-Order Dynamic Systems: Stability, Simulation, Applications and Perspectives, Springer, New York, 2012. [30] E. Kreyszig, Introductory Functional Analysis with Applications, Wiley, New York, 1978. [31] C. Li and F. Zeng, Numerical Methods for Fractional Calculus, Chapman and Hall/CRC, New York, 2015. [32] L. Li, F. Liu, L. Feng and I. Turner, A Galerkin finite element method for the modified distributed-order anomalous sub-diffusion equation, J. Comput. Appl. Math., 2020, 368, 112589. doi: 10.1016/j.cam.2019.112589 [33] Y. Lin and W. Jiang, Numerical method for Stokes' first problem for a heated generalized second grade fluid with fractional derivative, Numer. Methods Partial Differential Equations, 2011, 27, 1599–1609. doi: 10.1002/num.20598 [34] S. Mashayekhi, Y. Ordokhani and M. Razzaghi, Hybrid functions approach for nonlinear constrained optimal control problems, Commun. Nonlinear Sci. Numer. Simul., 2012, 17, 1831–1843. doi: 10.1016/j.cnsns.2011.09.008 [35] S. Mashayekhi and M. Razzaghi, Numerical solution of distributed-order fractional differential equations by hybrid functions, J. Comput. Phys., 2016, 315, 169–181. doi: 10.1016/j.jcp.2016.01.041 [36] A. Mohebbi, M. Abbaszadeh and M. Dehghan, Compact finite difference scheme and RBF meshless approach for solving 2D Rayleigh–Stokes problem for a heated generalized second grade fluid with fractional derivatives, Comput. Methods Appl. Mech. Engrg., 2013, 264, 163–177. doi: 10.1016/j.cma.2013.05.012 [37] M. L. Morgado and M. Rebelo, Numerical approximation of distributed-order reaction-diffusion equations, J. Comput. Appl. Math., 2015, 275, 216–227. doi: 10.1016/j.cam.2014.07.029 [38] M. L. Morgado, M. Rebelo, L. L. Ferrás and N. J. Ford, Numerical solution for diffusion equations with distributed-order in time using a Chebyshev collocation method, Appl. Numer. Math., 2017, 114, 108–123. doi: 10.1016/j.apnum.2016.11.001 [39] V. G. Pimenov, A. S. Hendy and R. H. De Staelen, On a class of non-linear delay distributed-order fractional diffusion equations, J. Comput. Appl. Math., 2017, 318, 433–443. doi: 10.1016/j.cam.2016.02.039 [40] I. Podulbny, Fractional Differential Equations, Academic Press, New York, 1999. [41] M. Pourbabaee and A. Saadatmandi, A novel Legendre operational matrix for distributed-order fractional differential equations, Appl. Math. Comput., 2019, 361, 215–231. [42] M. Pourbabaee and A. Saadatmandi, A new operational matrix based on Müntz-Legendre polynomials for solving distributed-order fractional differential equations, Math. Comput. Simulation, 2022, 194, 210–235. doi: 10.1016/j.matcom.2021.11.023 [43] P. Rahimkhani, Y. Ordokhani and E. Babolian, Fractional-order Bernoulli functions and their applications in solving fractional Fredholem-Volterra integro-differential equations, Appl. Numer. Math., 2017, 122, 66-81. doi: 10.1016/j.apnum.2017.08.002 [44] T. J. Rivlin, An Introduction to the Approximation of Functions, Dover Publications, New York, 1981. [45] A. Saadatmandi, A. Khani and M. R. Azizi, Numerical calculation of fractional derivatives for the Sinc functions via Legendre polynomials, Math. Interdisc. Res., 2020, 5, 71–86. [46] N. Samadyar and F. Mirzaee, Orthonormal Bernoulli polynomials collocation approach for solving stochastic Itô-Volterra integral equations of Abel type, Int. J. Numer. Model., 2019, 33, e2688. [47] F. Shen, W. C. Tan, Y. Zhao and T. Masuoka, The Rayleigh-Stokes problem for a heated generalized second grade fluid with fractional derivative model, Nonlinear Anal. Real World Appl., 2006, 7, 1072–1080. doi: 10.1016/j.nonrwa.2005.09.007 [48] E. Shivanian and A. Jafarabadi, Rayleigh-Stokes problem for a heated generalized second grade fluid with fractional derivatives: a stable scheme based on spectral meshless radial point interpolation, Eng Comput., 2018, 34, 77–90. doi: 10.1007/s00366-017-0522-1 [49] U. P. Singh, Application of orthonormal Bernoulli polynomials for approximate solution of some Volterra integral equations, Albanian J. Math., 2016, 10, 47–80. [50] C. Wu, Numerical solution for Stokes' first problem for a heated generalized second grade fluid with fractional derivative, Appl. Numer. Math., 2009, 59, 2571–2583. doi: 10.1016/j.apnum.2009.05.009 [51] X. Yang and X. Jiang, Numerical algorithm for two dimensional fractional Stokes' first problem for a heated generalized second grade fluid with smooth and non-smooth solution, Comput. Math. Appl., 2019, 78, 1562–1571. [52] C. Ye, X. N. Luo and L. P. Wen, High-order numerical methods of fractional-order Stokes' first problem for heated generalized second grade fluid, Appl. Math. Mech. (English Ed.), 2012, 33, 65–80. doi: 10.1007/s10483-012-1534-8 [53] H. Ye, F. Liu and V. Anh, Compact difference scheme for distributed-order time-fractional diffusion-wave equation on bounded domains, J. Comput. Phys., 2015, 298, 652–660. doi: 10.1016/j.jcp.2015.06.025 [54] H. Ye, F. Liu, V. Anh and I. Turner, Numerical analysis for the time distributed-order and Riesz space fractional diffusions on bounded domains, IMA J. Appl. Math., 2015, 80, 825–838. doi: 10.1093/imamat/hxu015 [55] M. A. Zaky, An improved tau method for the multi-dimensional fractional Rayleigh-Stokes problem for a heated generalized second grade fluid, Comput. Math. Appl., 2018, 75, 2243–2258. -
-
-
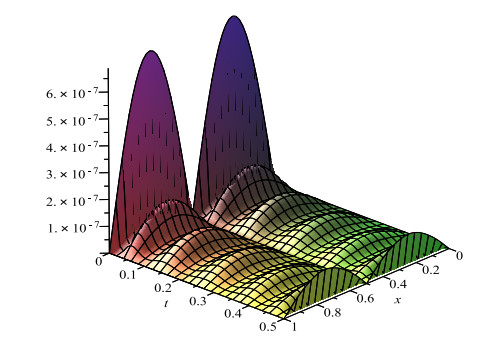
Figure 1.
The absolute error function for
$ {R}=4, Y=6 $ -
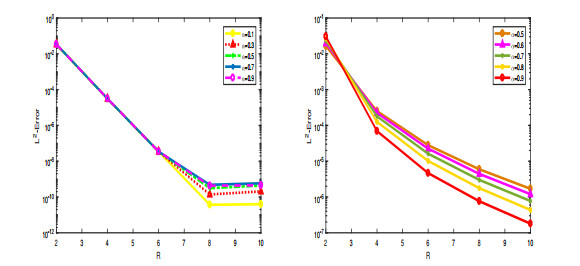
Figure 2.
The
$ L^2 $ -
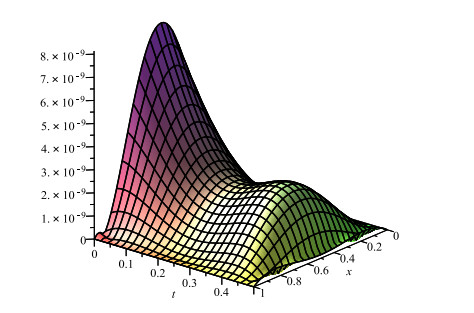
Figure 3.
The absolute error function with
$ {R}=13, Y=5 $




 DownLoad:
DownLoad: