| Citation: | Jin Wen, Chong-Wang Yue, Zhuan-Xia Liu, Donal O'Regan. A FRACTIONAL LANDWEBER ITERATION METHOD FOR SIMULTANEOUS INVERSION IN A TIME-FRACTIONAL DIFFUSION EQUATION[J]. Journal of Applied Analysis & Computation, 2023, 13(6): 3374-3402. doi: 10.11948/20230051 |
A FRACTIONAL LANDWEBER ITERATION METHOD FOR SIMULTANEOUS INVERSION IN A TIME-FRACTIONAL DIFFUSION EQUATION
-
Abstract
In the present paper, we study the problem to identify the space-dependent source term and initial value simultaneously for a time-fractional diffusion equation. This inverse problem is ill-posed, and we use the idea of decoupling to turn it into two operator equations based on the Fourier method. To solve the inverse problem, a fractional Landweber regularization method is proposed. Furthermore, we present convergence estimates between the exact solution and the regularized solution by using the a-priori and the a-posteriori parameter choice rules. In order to verify the accuracy and efficiency of the proposed method, several numerical examples are constructed.
-

-
References
[1] O. P. Agrawal, Solution for a fractional diffusion-wave equation defined in a bounded domain, Fractional Order Calculus and its Applications, 2002, 145–155. [2] A. Babaei, Solving a time-fractional inverse heat conduction problem with an unknown nonlinear boundary condition, J. Math. Model., 2019, 7(1), 85–106. [3] B. Berkowitz, H. Scher and S. E. Silliman, Anomalous transport in laboratory-scale, heterogeneous porous media, Water Resources Research, 2000, 36(1), 149–158. doi: 10.1029/1999WR900295 [4] A. Chen and C. Li, Numerical solution of fractional diffusion-wave equation, Numer. Funct. Anal. Optim., 2016, 37(1), 19–39. doi: 10.1080/01630563.2015.1078815 [5] R. Courant and D. Hilbert, Methods of mathematical physics - vol. 1; vol. 2, New York Interscience Publication, 1953, 305(3–4), 121–132. [6] R. Du, W. R. Cao and Z. Z. Sun, A compact difference scheme for the fractional diffusion-wave equation, Appl. Math. Model., 2010, 34(10), 2998–3007. doi: 10.1016/j.apm.2010.01.008 [7] H. Egger and A. Neubauer, Preconditioning Landweber iteration in Hilbert scales, Numer. Math., 2005, 101(4), 643–662. doi: 10.1007/s00211-005-0622-5 [8] H. W. Engl, M. Hanke and A. Neubauer, Regularization of inverse problems, 375 of Mathematics and its Applications, Kluwer Academic Publishers Group, Dordrecht, 1996. [9] M. Giona, S. Cerbelli and H. E. Roman, Fractional Diffusion Equation and Relaxation in Complex Viscoelastic Materials, Physica A Statistical Mechanics and its Applications, 1992. [10] Y. Han, X. Xiong and X. Xue, A fractional Landweber method for solving backward time-fractional diffusion problem, Comput. Math. Appl., 2019, 78(1), 81–91. [11] Y. Hatano and N. Hatano, Dispersive transport of ions in column experiments: An explanation of long-tailed profiles, Water Resources Research, 1998, 34(5), 1027–1034. doi: 10.1029/98WR00214 [12] L. N. Huynh, Y. Zhou, D. O'Regan and N. H. Tuan, Fractional Landweber method for an initial inverse problem for time-fractional wave equations, Appl. Anal., 2021, 100(4), 860–878. doi: 10.1080/00036811.2019.1622682 [13] H. Jiang, F. Liu, I. Turner and K. Burrage, Analytical solutions for the multi-term time-fractional diffusion-wave/diffusion equations in a finite domain, Comput. Math. Appl., 2012, 64(10), 3377–3388. [14] M. Jiang and G. Wang, Convergence studies on iterative algorithms for image reconstruction, IEEE Transactions on Medical Imaging, 2003, 22(5), 569–579. doi: 10.1109/TMI.2003.812253 [15] B. T. Johansson and D. Lesnic, A procedure for determining a spacewise dependent heat source and the initial temperature, Applicable Analysis, 2008, 87(3), 265–276. doi: 10.1080/00036810701858193 [16] E. Klann and R. Ramlau, Regularization by fractional filter methods and data smoothing, Inverse Problems, 2008, 24(2), 025018, 26. doi: 10.1088/0266-5611/24/2/025018 [17] L. Landweber, An iteration formula for Fredholm integral equations of the first kind, Amer. J. Math., 1951, 73, 615–624. doi: 10.2307/2372313 [18] X. Li and C. Xu, A space-time spectral method for the time fractional diffusion equation, SIAM J. Numer. Anal., 2009, 47(3), 2108–2131. doi: 10.1137/080718942 [19] Y. Lin and C. Xu, Finite difference/spectral approximations for the time-fractional diffusion equation, J. Comput. Phys., 2007, 225(2), 1533–1552. doi: 10.1016/j.jcp.2007.02.001 [20] A. K. Louis, Inverse und Schlecht Gestellte Probleme, Teubner Studienbücher Mathematik. [Teubner Mathematical Textbooks], B. G. Teubner, Stuttgart, 1989. [21] F. Mainardi, Fractional Diffusive Waves in Viscoelastic Solids, 1995. [22] R. Metzler and J. Klafter, Boundary value problems for fractional diffusion equations, Phys. A, 2000, 278(1–2), 107–125. doi: 10.1016/S0378-4371(99)00503-8 [23] A. Neubauer, On Landweber iteration for nonlinear ill-posed problems in Hilbert scales, Numer. Math., 2000, 85(2), 309–328. doi: 10.1007/s002110050487 [24] I. Podlubny, Fractional Differential Equations, 198 of Mathematics in Science and Engineering, Academic Press, Inc., San Diego, CA, 1999. An introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. [25] C. Ren, X. Xu and S. Lu, Regularization by projection for a backward problem of the time-fractional diffusion equation, J. Inverse Ill-Posed Probl., 2014, 22(1), 121–139. doi: 10.1515/jip-2011-0021 [26] H. E. Roman and P. A. Alemany, Continuous-time random walks and the fractional diffusion equation, J. Phys. A, 1994, 27(10), 3407–3410. doi: 10.1088/0305-4470/27/10/017 [27] Z. Ruan, J. Z. Yang and X. Lu, Tikhonov regularisation method for simultaneous inversion of the source term and initial data in a time-fractional diffusion equation, East Asian J. Appl. Math., 2015, 5(3), 273–300. doi: 10.4208/eajam.310315.030715a [28] Z. Ruan and S. Zhang, Simultaneous inversion of time-dependent source term and fractional order for a time-fractional diffusion equation, J. Comput. Appl. Math., 2020, 368, 112566, 15. doi: 10.1016/j.cam.2019.112566 [29] K. Sakamoto and M. Yamamoto, Initial value/boundary value problems for fractional diffusion-wave equations and applications to some inverse problems, J. Math. Anal. Appl., 2011, 382(1), 426–447. doi: 10.1016/j.jmaa.2011.04.058 [30] I. M. Sokolov and J. Klafter, From diffusion to anomalous diffusion: a century after Einstein's Brownian motion, Chaos, 2005, 15(2), 026103, 7. doi: 10.1063/1.1860472 [31] L. L. Sun, Y. S. Li and Y. Zhang, Simultaneous inversion of the potential term and the fractional orders in a multi-term time-fractional diffusion equation, Inverse Problems, 2021, 37(5), Paper No. 055007, 26. [32] N. H. Tuan, L. N. Huynh, T. B. Ngoc and Y. Zhou, On a backward problem for nonlinear fractional diffusion equations, Appl. Math. Lett., 2019, 92, 76–84. doi: 10.1016/j.aml.2018.11.015 [33] G. M. Vainikko and A. Y. Veretennikov, Iteration Procedures in Ill-Posed Problems, Nauka, Moscow, 1986. [34] J. -G. Wang and T. Wei, An iterative method for backward time-fractional diffusion problem, Numer. Methods Partial Differential Equations, 2014, 30(6), 2029–2041. doi: 10.1002/num.21887 [35] J. Wen, Z. -X. Liu and S. -S. Wang, Conjugate gradient method for simultaneous identification of the source term and initial data in a time-fractional diffusion equation, Applied Mathematics in Science and Engineering, 2022, 30(1), 324–338. doi: 10.1080/27690911.2022.2075358 [36] J. Wen, Z. -X. Liu, C. -W. Yue and S. -J. Wang, Landweber iteration method for simultaneous inversion of the source term and initial data in a time-fractional diffusion equation, J. Appl. Math. Comput., 2022, 68(5), 3219–3250. doi: 10.1007/s12190-021-01656-0 [37] J. Wen, X. -J. Ren and S. -J. Wang, Simultaneous determination of source term and initial value in the heat conduction problem by modified quasi-reversibility regularization method, Numerical Heat Transfer, Part B: Fundamentals, 2022, 82(3–4), 112–127. doi: 10.1080/10407790.2022.2079281 [38] J. Wen, C. -W. Yue, Z. -X. Liu and S. -J. Wang, Fractional tikhonov regularization method for simultaneous inversion of the source term and initial data in a time-fractional diffusion equation, Rocky Mountain Journal of Mathematics, 2023, 53(1), 249–273. [39] X. -T. Xiong, X. -M. Xue and Z. Qian, A modified iterative regularization method for ill-posed problems, Appl. Numer. Math., 2017, 122, 108–128. doi: 10.1016/j.apnum.2017.08.004 [40] F. Yang, J. -L. Fu, P. Fan and X. -X. Li, Fractional Landweber iterative regularization method for identifying the unknown source of the time-fractional diffusion problem, Acta Appl. Math., 2021, 175, Paper No. 13, 19. [41] F. Yang, X. Liu, X. -X. Li and C. -Y. Ma, Landweber iterative regularization method for identifying the unknown source of the time-fractional diffusion equation, Adv. Difference Equ., 2017, Paper No. 388, 15. [42] F. Yang, Y. -P. Ren, X. -X. Li and D. -G. Li, Landweber iterative method for identifying a space-dependent source for the time-fractional diffusion equation, Bound. Value Probl., 2017, Paper No. 163, 19. [43] F. Yang, Y. Zhang and X. -X. Li, Landweber iterative method for identifying the initial value problem of the time-space fractional diffusion-wave equation, Numerical Algorithms, 2020, 83(4), 1509–1530. doi: 10.1007/s11075-019-00734-6 [44] L. Yang, Z. -C. Deng and Y. -C. Hon, Simultaneous identification of unknown initial temperature and heat source, Dynam. Systems Appl., 2016, 25(4), 583–602. [45] Y. Zhang, T. Wei and Y. -X. Zhang, Simultaneous inversion of two initial values for a time-fractional diffusion-wave equation, Numer. Methods Partial Differential Equations, 2021, 37(1), 24–43. doi: 10.1002/num.22517 [46] Y. Zhou, J. Wei He, B. Ahmad and N. Huy Tuan, Existence and regularity results of a backward problem for fractional diffusion equations, Mathematical Methods in the Applied Sciences, 2019, 42(18), 6775–6790. -
-
-
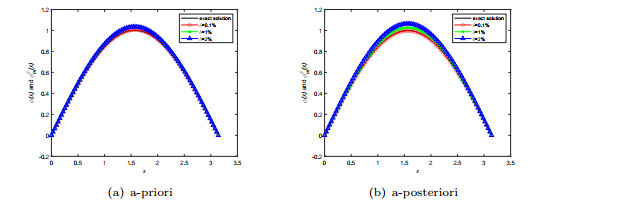
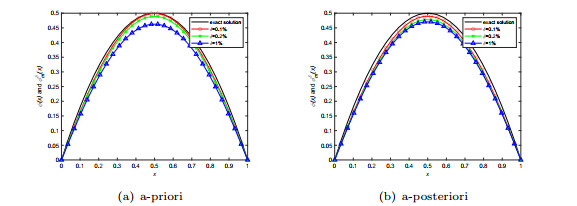
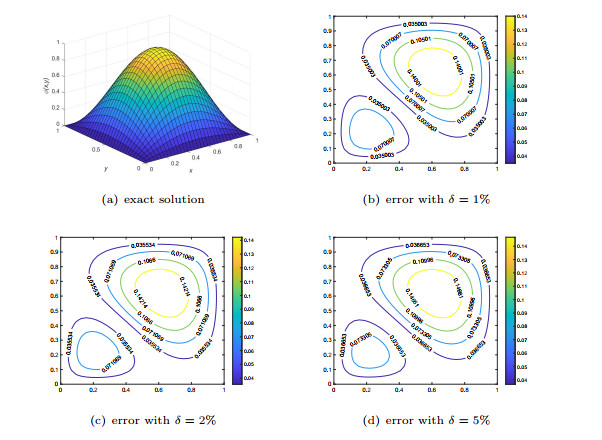
Figure 1.
Numerical results for source term in Example 1
-
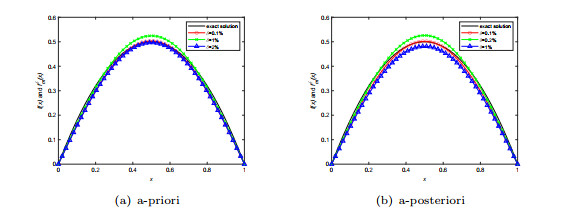
Figure 2.
Numerical results for initial term in Example 1
-
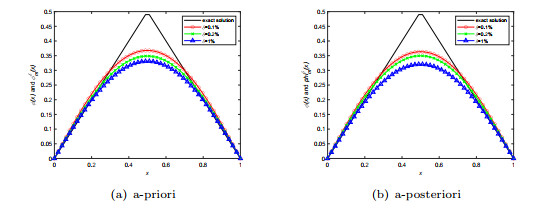
Figure 3.
Numerical results for source term in Example 2
-
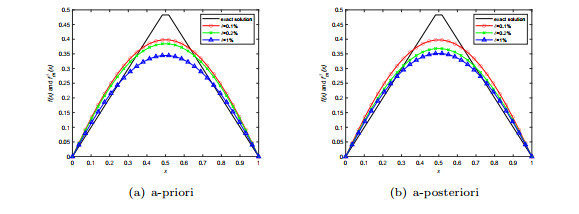
Figure 4.
Numerical results for initial term in Example 2
-
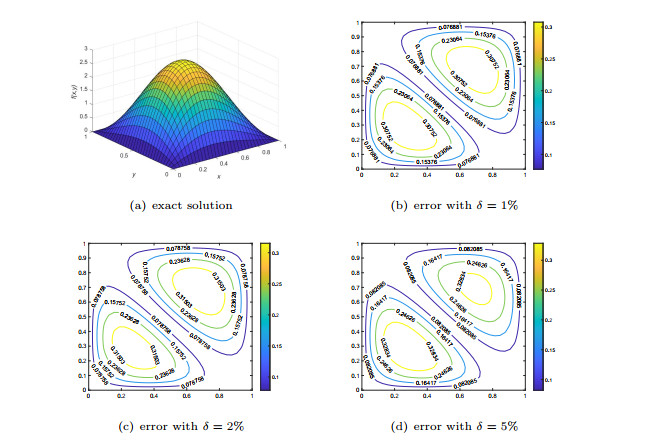
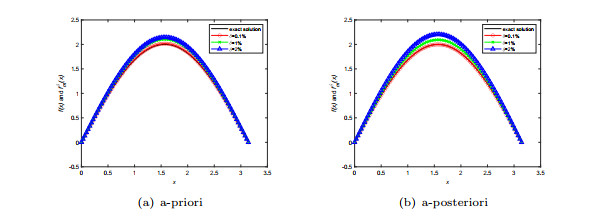
Figure 5.
Numerical results for source term in Example 3
-
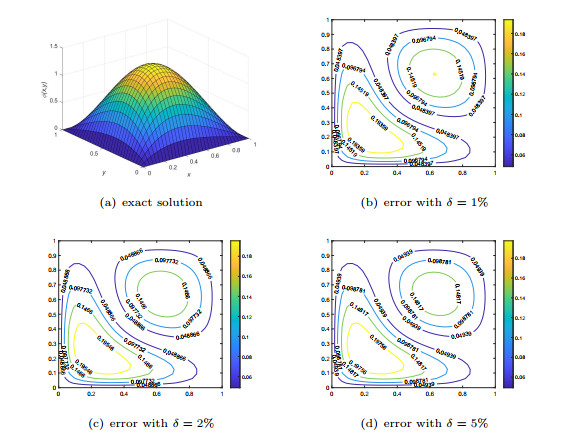
Figure 6.
Numerical results for initial term in Example 3
-
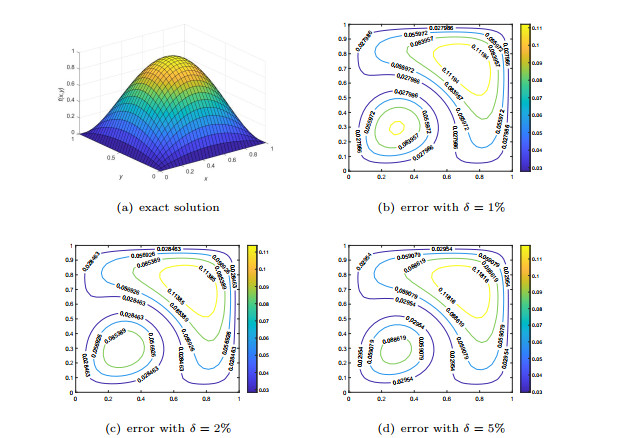
Figure 7.
Numerical results for source term in Example 4
-
Figure 8.
Numerical results for source term in Example 4
-
Figure 9.
Numerical results for source term in Example
$ 5 $ -
Figure 10.
Numerical results for initial term in Example
$ 5 $




 DownLoad:
DownLoad: