| Citation: | Hajri Imen, Fethi Ben Belgacem. CONVERGENT APPROACHES FOR THE DIRICHLET MONGE-AMPÈRE PROBLEM[J]. Journal of Applied Analysis & Computation, 2024, 14(1): 146-161. doi: 10.11948/20230104 |
CONVERGENT APPROACHES FOR THE DIRICHLET MONGE-AMPÈRE PROBLEM
-
Abstract
In this article, we introduce and study three numerical methods for the Dirichlet Monge-Ampère equation in two dimensions. The approaches consist in considering new equivalent problems. In the first method (method A) the equivalent problem is discretized by a wide stencil finite difference discretization and monotone schemes are obtained. Hence, we apply the Barles-Souganidis theory to prove the convergence of the schemes and the Damped Newtons method is used to compute the solutions of the schemes. In the last two methods (B and C) we introduce two fixed point operators. Finally, some numerical results are illustrated.
-
Keywords:
- Monge-Ampère /
- fixed point /
- wide stencil /
- Newton method
-

-
References
[1] G. Barles and P. E. Souganidis, Convergence of approximation schemes for fully nonlinear second order equations, Asymptotic Anal., 1991, 4(3), 271–283. doi: 10.3233/ASY-1991-4305 [2] F. B. Belgacem, Optimization approach for the Monge-Ampère equation, Acta Mathematica Scientia., 2018, 38(4), 1285–1295. doi: 10.1016/S0252-9602(18)30814-2 [3] J. D. Benamou, B. D. Froese and A. M. Oberman, Two numerical methods for the elliptic Monge-Ampère equation, ESAIM: Math. Model. Numer. Anal., 2010, 44(4), 271–293. [4] R. J. Berman, Convergence rates for discretized Monge-Ampère equations and quantitative stability of optimal transport, Found Comput. Math., 2021, 21, 1099–1140. doi: 10.1007/s10208-020-09480-x [5] M. W. M. C. Bertens, et al., Numerical methods for the hyperbolic Monge-Ampère equation based on the method of characteristics, Partial Differential Equations and Applications, 2022, 52(3), 1–42. [6] G. Bonnet and J. M. Mirebeau, Monotone discretization of the Monge-Ampère equation of optimal transport, ESAIM: M2AN., 2022, 56, 815–865. doi: 10.1051/m2an/2022029 [7] C. J. Budd and J. F. Williams, Moving mesh generation using the parabolic Monge-Ampère equation, SIAM J. Sci. Comput., 2009, 31(5), 3438–3465. doi: 10.1137/080716773 [8] E. Calabi, Complete affine hyperspheres. I, Symposia Mathematica., 1972, 10, 19–38. [9] S. Y. Cheng and S. T. Yau, Complete affine hypersurfaces. I. The completeness of affine metrics, Comm. Pure Appl. Math., 1986, 39(6), 839–866. doi: 10.1002/cpa.3160390606 [10] E. J. Dean and R. Glowinski, An augmented Lagrangian approach to the numerical solution of the Dirichlet problem for the elliptic Monge-Ampère equation in two dimensions, Electron. Trans. Numer. Anal., 2006, 22, 779–784. [11] E. J. Dean and R. Glowinski, On the numerical solution of the elliptic Monge-Ampère equation in dimension two: A least-squares approach, in Partial differential equations, 2008, 16, 887–892. [12] E. J. Dean and R. Glowinski, Numerical methods for fully nonlinear elliptic equations of the Monge-Ampère type, Comput. Methods Appl. Mech. Engrg., 2006, 195(13–16), 1344–1386. doi: 10.1016/j.cma.2005.05.023 [13] G. L. Delzanno, et al., An optimal robust equidistribution method for two-dimensional grid adaptation based on Monge-Kantorovich optimization, J. Comput. Phys., 2008, 227(23), 9841–9864. doi: 10.1016/j.jcp.2008.07.020 [14] X. Feng and M. Neilan, Mixed finite element methods for the fully nonlinear Monge-Ampère equation based on the vanishing moment method, SIAM J. Numer. Anal., 2009, 47(2), 1226–1250. doi: 10.1137/070710378 [15] J. M. Finn, et al., Grid generation and adaptation by Monge-Kantorovich optimization in two and three dimensions, in Proceedings of the 17th International Meshing Roundtable, 2008, 551–568. [16] B. D. Froese and A. M. Oberman, Convergent finite difference solvers for viscosity solutions of the elliptic Monge-Ampère equation in dimensions two and higher, SIAM J. Numer. Anal., 2011, 49, 1692–1714. doi: 10.1137/100803092 [17] T. Glimm and V. Oliker, Optical design of single reflector systems and the Monge-Kantorovich mass transfer problem, J. Math. Sci. (N. Y. ), 2003, 117(3), 4096–4108. doi: 10.1023/A:1024856201493 [18] C. E. Gutiérrez, The Monge-Ampère equation, Progress in Nonlinear Differential Equations and their Applications, 2001, 44, 31–43. [19] S. Haker, et al., Mass preserving mappings and image registration, in MICCAI '01: Proceedings of the 4th International Conference on Medical Image Computing and Computer-Assisted Intervention, 2001, 120–127. [20] S. Haker, et al., Optimal mass transport for registration and warping, Int. J. Comput. Vision, 2004, 60(3), 225–240. doi: 10.1023/B:VISI.0000036836.66311.97 [21] Q. Li and Z. Liu, Cascadic Newton's method for the elliptic Monge-Ampère equation, International Journal of Wavelets, Multiresolution and Information Processing, 2020, 18(3), 990–996. [22] H. Liu, S. Leung and J. Qian, An efficient operator-splitting method for the eigenvalue problem of the Monge-Ampère equation, Commun. Optim. Theory, 2022, 1–22. [23] R. H. Nochetto, D. Ntogkas and W. Zhang, Two-scale method for the Monge-Ampère equation: Convergence to the viscosity solution, Mathematics of computation, 2019, 88(316), 1085–1109. [24] A. M. Oberman, Convergent difference schemes for degenerate elliptic and parabolic equations: Hamilton-Jacobi equations and free boundary problems, SIAM J. Numer. Anal., 2006, 44(2), 879–895. doi: 10.1137/S0036142903435235 [25] A. M. Oberman, Computing the convex envelope using a nonlinear partial differential equation, Math. Models Methods Appl. Sci., 2008, 18(5). [26] A. M. Oberman, Wide stencil finite difference schemes for the elliptic Monge-Ampère equation and functions of the eigenvalues of the Hessian, Discrete Contin. Dyn. Syst. Ser. B, 2008, 10(1), 221–238. [27] A. M. Oberman and L. Silvestre, The Dirichlet problem for the convex envelope, Trans. Amer. Math. Soc., 2010, 363(11), 5871–5886. [28] V. I. Oliker and L. D. Prussner, On the numerical solution of the equation $\frac{\partial^2 z}{\partial x^2} \frac{\partial^2 z}{\partial y^2} - \left(\frac{\partial^2 z}{\partial x \partial y}\right)^2 = f$ and its discretizations, I, Numer. Math., 1988, 54(3), 271–293. [29] G. D. Philippis and A. Figalli, The Monge-Ampère equation and its link to optimal transportation, Bull. Amer. Math. Soc. (N. S. ), 2014, 51(4), 33–46. [30] A. V. Pogorelov, On the improper convex affine hyperspheres, Geometriae Dedicata, 1972, 1(1). [31] T. U. Rehman, et al., 3D nonrigid registration via optimal mass transport on the GPU, Med Image Anal, 2009, 13(6), 931–940. doi: 10.1016/j.media.2008.10.008 [32] J. Siltakoski, Equivalence of viscosity and weak solutions for the normalized $p(x)$-Laplacian, Calc. Var., 2018, 57. [33] N. S. Trudinger and X. -J. Wang, The Bernstein problem for affine maximal hypersurfaces, Invent. Math., 2000, 140(2), 399–422. doi: 10.1007/s002220000059 [34] N. S. Trudinger and X. -J. Wang, Affine complete locally convex hypersurfaces, Invent. Math., 2002, 150(1), 45–60. doi: 10.1007/s00222-002-0229-8 [35] N. S. Trudinger and X. -J. Wang, The affine Plateau problem, J. Amer. Math. Soc., 2005, 18(2), 253–289. doi: 10.1090/S0894-0347-05-00475-3 [36] V. Zheligovsky, et al., The Monge-Ampère equation: Various forms and numerical solution, J. Comput. Phys., 2010, 229(13), 5043–5061. doi: 10.1016/j.jcp.2010.03.025 -
-
-
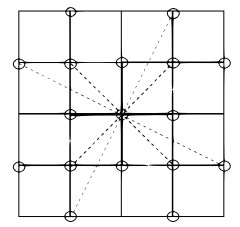
Figure 1.
Grid for wide stencil 17 points, in two dimension.
-
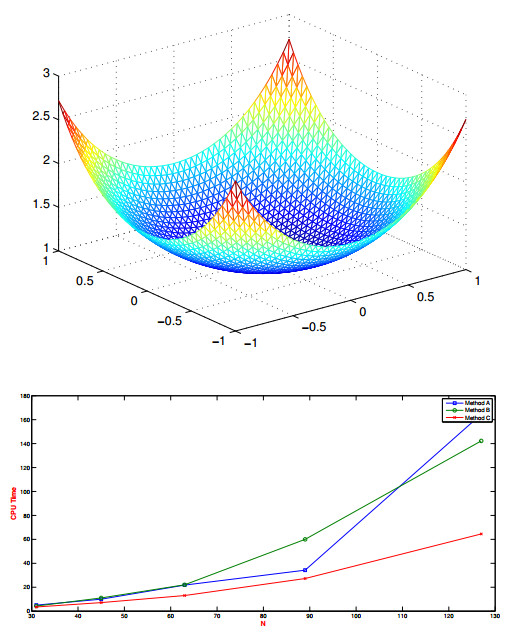
Figure 2.
Results for the first example on an
$ N\times N $ $ N $ -
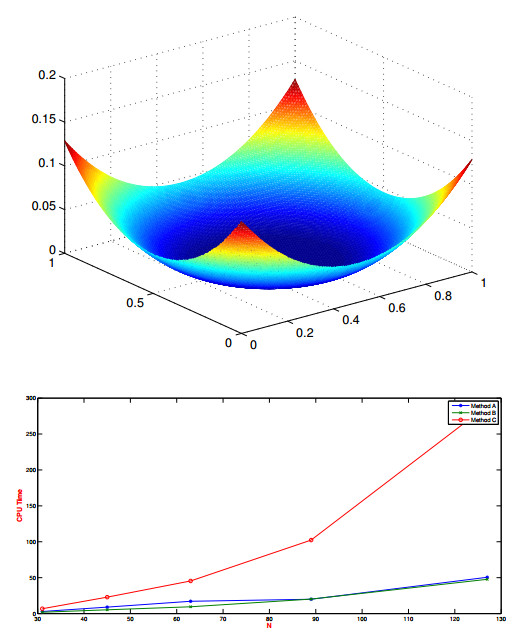
Figure 3.
Results for the second example on an
$ N\times N $ $ N $ -
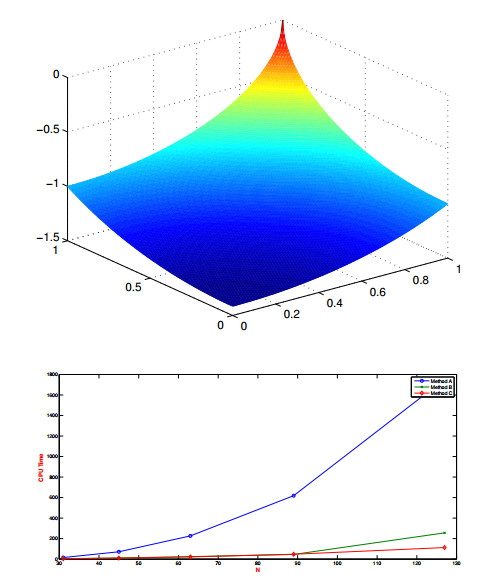
Figure 4.
Results for the third example on an
$ N\times N $ $ N $




 DownLoad:
DownLoad: