| Citation: |
Wenbin Bao, Shuxin Miao. A MODIFIED BLOCK PRECONDITIONER FOR COMPLEX SYMMETRIC INDEFINITE LINEAR SYSTEMS[J]. Journal of Applied Analysis & Computation, 2024, 14(1): 182-196. doi: 10.11948/20230131
|
A MODIFIED BLOCK PRECONDITIONER FOR COMPLEX SYMMETRIC INDEFINITE LINEAR SYSTEMS
-
Abstract
To solve the real equivalent $ 2\times 2 $ block linear system of complex symmetric indefinite linear systems, by introducing a preconditioning matrix in the NB preconditioner (which was proposed in [Numerical Algorithm, 74 (2017) 889-903]), a modified block preconditioner is proposed. Compared with the NB one, when choose a suitable preconditioning matrix for the new preconditioner to get faster convergence than the NB preconditioner. The unconditional convergence of the new iteration method is discussed. The eigenvalue distribution and an upper bound of the degree of the minimal polynomial of the preconditioned matrix are given. Finally, a numerical example is carried out to demonstrate the effectiveness and robustness of the proposed preconditioner.
-
-
References
[1] S. R. Arridge, Optical tomography in medical imaging, Inverse Probl., 1999, 15, 41–93. doi: 10.1088/0266-5611/15/1/008 [2] O. Axelsson and A. Kucherov, Real valued iterative methods for solving complex symmetric linear systems, Numer. Linear Algebra Appl., 2000, 7, 197–218. doi: 10.1002/1099-1506(200005)7:4<197::AID-NLA194>3.0.CO;2-S [3] O. Axelsson, M. Neytcheva and B. Ahmad, A comparison of iterative methods to solve complex valued linear algebraic systems, Numer. Algor., 2014, 66, 811–841. doi: 10.1007/s11075-013-9764-1 [4] O. Axelsson, M. Pourbagher and D. K. Salkuyeh, Efficient iteration methods for complex systems with an indefinite matrix term, Calcolo, 2022, 59, 15. doi: 10.1007/s10092-022-00461-w [5] Z. Bai, Sharp error bounds of some Krylov subspace methods for non-Hermitian linear systems, Appl. Math. Comput., 2000, 109, 273–285. [6] Z. Bai, Motivations and realizations of Krylov subspace methods for large sparse linear systems, J. Comput. Appl. Math., 2015, 283, 71–78. doi: 10.1016/j.cam.2015.01.025 [7] Z. Bai, G. H. Golub and M. K. Ng, Hermitian and skew-Hermitian splitting methods for non-Hermitian positive definite linear systems, SIAM J. Matrix Anal. Appl., 2003, 24, 603–626. doi: 10.1137/S0895479801395458 [8] Z. Bai and A. Hadjidimos, Optimization of extrapolated Cayley transform with non-Hermitian positive definite matrix, Linear Algebra Appl., 2014, 463, 322–339. doi: 10.1016/j.laa.2014.08.021 [9] F. B. Balani and M. Hajarian, On the generalized AOR and CG iteration methods for a class of block two-by-two linear systems, Numer. Algor., 2022, 90, 669–685. doi: 10.1007/s11075-021-01203-9 [10] W. Bao, An improved preconditioner for $2 \times 2$ block linear system arising from complex linear system, Japan J. Indust. Appl. Math., 2021, 38, 859–875. doi: 10.1007/s13160-021-00463-1 CrossRef $2 \times 2$ block linear system arising from complex linear system" target="_blank">Google Scholar
[11] M. Benzi and D. Bertaccini, Block preconditioning of real-valued iterative algorithms for complex linear systems, IMA J. Numer. Anal., 2008, 28, 598–618. [12] D. Bertaccini, Efficient solvers for sequences of complex symmetric linear systems, Electron. Trans. Numer. Anal., 2004, 18, 49–64. [13] Y. Cao, J. Du and Q. Niu, Shift-splitting preconditioners for saddle point problems, J. Comput. Appl. Math., 2014, 272, 239–250. doi: 10.1016/j.cam.2014.05.017 [14] Y. Cao and Z. Ren, Two variants of the PMHSS iteration method for a class of complex symmetric indefinite linear systems, Appl. Math. Comput., 2015, 264, 61–71. [15] F. Chen, On convergence of EVHSS iteration method for solving generalized saddle-point linear systems, Appl. Math. Lett., 2018, 86, 30–35. doi: 10.1016/j.aml.2018.06.001 [16] K. Chen, Matrix Preconditioning Techniques and Applications, Cambridge University Press, Cambridge, 2005. [17] D. Day and M. A. Heroux, Solving complex-valued linear systems via equivalent real formulations, SIAM J. Sci. Comput., 2001, 23(2), 480–498. doi: 10.1137/S1064827500372262 [18] B. B. Fariba and H. Masoud, Modified block product preconditioner for a class of complex symmetric linear systems, Linear Multilinear Algebra., 2023, 71, 1521–1535. doi: 10.1080/03081087.2022.2065231 [19] A. Feriani, F. Perotti and V. Simoncini, Iterative system solvers for the frequency analysis of linear mechanical systems, Comput. Methods Appl. Mech. Engrg., 2000, 190, 1719–1739. doi: 10.1016/S0045-7825(00)00187-0 [20] D. Hezari, V. Edalatpour and D. K Salkuyeh, Preconditioned GSOR iterative method for a class of complex symmetric system of linear equations, Numer. Linear Algebra Appl., 2015, 22, 338–356. doi: 10.1002/nla.1952 [21] V. E. Howle and S. A. Vavasis, An iterative method for solving complex-symmetric systems arising in electrical power modeling, SIAM J. Matrix Anal. Appl., 2005, 26, 1150–1178. doi: 10.1137/S0895479800370871 [22] Y. Huang, A practical formula for computing optimal parameters in the HSS iteration methods, J. Comput. Appl. Math., 2014, 225, 142–149. [23] Z. Liang, O. Axelsson and G. Zhang, Efficient iterative solvers for a complex valued two-by-two block linear system with application to parabolic optimal control problems, Appl. Numer. Math., 2020, 152, 422–445. doi: 10.1016/j.apnum.2019.11.011 [24] Z. Liang and G. Zhang, On SSOR iteration method for a class of block two-by-two linear systems, Numer. Algor., 2016, 71, 655–671. doi: 10.1007/s11075-015-0015-5 [25] S. Miao, A new preconditioner for a class of $2 \times 2$ block linear systems, Japan J. Indust. Appl. Math., 2020, 37, 913–928. doi: 10.1007/s13160-020-00425-z CrossRef $2 \times 2$ block linear systems" target="_blank">Google Scholar
[26] M. Pourbagher and D. K. Salkuyeh, A new two-parameter iteration method for indefinite complex symmetric linear systems, Japan J. Indust. Appl. Math., 2022, 39, 145–163. doi: 10.1007/s13160-021-00479-7 [27] Y. Saad, Iterative Methods for Sparse Linear Systems, SIAM, Philadephia, 2003. [28] Y. Saad and M. H. Schultz, GMRES: A generalised minimal residual algorithm for solving nonsymmetric linear systems, SIAM J. Sci. Stat. Comput., 1986, 7(3), 856–869. doi: 10.1137/0907058 [29] Q. Shen and Q. Shi, A variant of the HSS preconditioner for complex symmetric indefinite linear systems, Comput. Math. Appl., 2018, 75, 850–863. doi: 10.1016/j.camwa.2017.10.006 [30] T. Wang and L. Lu, Alternating-directional PMHSS iteration method for a class of two-by-two block linear systems, Appl. Math. Lett., 2016, 58, 159–164. doi: 10.1016/j.aml.2016.02.014 [31] J. Zhang and H. Dai, A new block preconditioner for complex symmetric indefinite linear systems, Numer. Algor., 2017, 74, 889–903. doi: 10.1007/s11075-016-0175-y [32] Q. Zheng and L. Lu, A shift-splitting preconditioner for a class of block two-by-two linear systems, Appl. Math. Lett., 2017, 66, 54–60. doi: 10.1016/j.aml.2016.11.009 -
-
Figures(2) / Tables(2)
Export File
Citation
Wenbin Bao, Shuxin Miao. A MODIFIED BLOCK PRECONDITIONER FOR COMPLEX SYMMETRIC INDEFINITE LINEAR SYSTEMS[J]. Journal of Applied Analysis & Computation, 2024, 14(1): 182-196. doi: 10.11948/20230131
Format
Content
DownLoad:
-
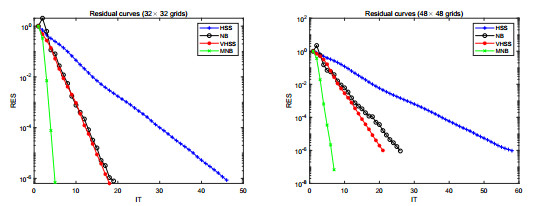
Figure 1.
Residual curves of different preconditioned iteration methods for Example 4.1:
$ 32\times 32 $ $ 48\times 48 $ -
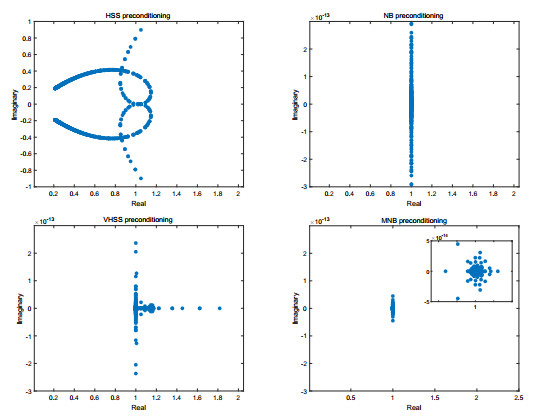
Figure 2.
The eigenvalue distributions of preconditioned matrices for Example 4.1