| Citation: |
Nauman Raza, Syeda Sarwat Kazmi, Ghada Ali Basendwah. DYNAMICAL ANALYSIS OF SOLITONIC, QUASI-PERIODIC, BIFURCATION AND CHAOTIC PATTERNS OF LANDAU-GINZBURG-HIGGS MODEL[J]. Journal of Applied Analysis & Computation, 2024, 14(1): 197-213. doi: 10.11948/20230137
|
DYNAMICAL ANALYSIS OF SOLITONIC, QUASI-PERIODIC, BIFURCATION AND CHAOTIC PATTERNS OF LANDAU-GINZBURG-HIGGS MODEL
-
Abstract
In this manuscript, the Landau-Ginzburg-Higgs (LGH) equation is considered as an investigating model. To extract novel results from the governing equation, the $ G'/(b G'+G+a) $-expansion approach has been employed. Utilizing this approach, the outcomes are attained as hyperbolic and trigonometric functions. Kink, periodic and singular soliton solutions have been recovered by selecting the appropriate values for the parameters. The obtained findings for the LGH equation are displayed in 3-D, contour and 2-D profiles. Using Galilean transformation, the model is converted into a planar dynamical system, and qualitative analysis is investigated. Moreover, chaotic and quasi-periodic patterns have been addressed after including the perturbed term. Simulated results reveal that by modifying amplitude and frequency parameters, the dynamic behavior of the system can also be changed. The recorded results are novel and show the effectiveness and feasibility of the suggested technique for assessing soliton solutions and phase visualizations for different nonlinear models.
-
-
References
[1] M. A. Abdou, An analytical method for space-time fractional nonlinear differential equations arising in plasma physics, Journal of Ocean Engineering and Science, 2017, 2(4), 288–292. doi: 10.1016/j.joes.2017.09.002 [2] T. Abdulkadir Sulaiman and A. Yusuf, Dynamics of lump-periodic and breather waves solutions with variable coefficients in liquid with gas bubbles, Waves in Random and Complex Media, 2021, 1–14. [3] G. Adomian, Solving frontier problems of physics: The decomposition method, Springer Science and Business Media, 2013, 60. [4] I. Ahmad, A. Jalil, A. Ullah, S. Ahmad and M. De la Sen, Some new exact solutions of (4+1)-dimensional Davey–-Stewartson-Kadomtsev–-Petviashvili equation, Results in Physics, 2023, 45, 106240. doi: 10.1016/j.rinp.2023.106240 [5] K. Ahmad, K. Bibi, M. S. Arif and K. Abodayeh, New Exact Solutions of Landau-Ginzburg-Higgs Equation Using Power Index Method, Journal of Function Spaces, 2023. [6] Ö. Z. E. R. Ahmet and A. K. I. N. Erhan, Tools for detecting chaos, Sakarya University Journal of Science, 2005, 9(1), 60–66. [7] L. Akinyemi, q-Homotopy analysis method for solving the seventh-order time-fractional LaxÂ's Korteweg–de Vries and Sawada–Kotera equations, Computational and Applied Mathematics, 2019, 38(4), 191. doi: 10.1007/s40314-019-0977-3 [8] L. Akinyemi, H. Rezazadeh, S. W. Yao, M. A. Akbar, M. M. Khater, A. Jhangeer, M. Inc and H. Ahmad, Nonlinear dispersion in parabolic law medium and its optical solitons, Results in Physics, 2021, 26, 104411. doi: 10.1016/j.rinp.2021.104411 [9] M. R. Ali, M. A. Khattab and S. M. Mabrouk, Travelling wave solution for the Landau-Ginburg-Higgs model via the inverse scattering transformation method, Nonlinear Dynamics, 2023, 1–11. [10] H. Almusawa, A. Jhangeer and Z. Hussain, Observation on different dynamics of breaking soliton equation by bifurcation analysis and multistability theory, Results in Physics, 2022, 36, 105364. doi: 10.1016/j.rinp.2022.105364 [11] M. F. Alotaibi, N. Raza, M. H. Rafiq and A. Soltani, New solitary waves, bifurcation and chaotic patterns of Fokas system arising in monomode fiber communication system, Alexandria Engineering Journal, 2023, 67,583–595. doi: 10.1016/j.aej.2022.12.069 [12] M. I. Asjad, S. Z. Majid, W. A. Faridi and S. M. Eldin, Sensitive analysis of soliton solutions of nonlinear Landau-Ginzburg-Higgs equation with generalized projective Riccati method, AIMS Mathematics, 2023, 8(5), 10210–10227. doi: 10.3934/math.2023517 [13] D. Baleanu, M. S. Osman, A. Zubair, N. Raza, O. A. Arqub and W. X. Ma, Soliton solutions of a nonlinear fractional Sasa-Satsuma equation in monomode optical fibers, Applied Mathematics and Information Sciences, 2020, 14(3), 365–374. doi: 10.18576/amis/140302 [14] O. A. Bruzzone, D. V. Perri and M. H. Easdale, Vegetation responses to variations in climate: A combined ordinary differential equation and sequential Monte Carlo estimation approach, Ecological Informatics, 2023, 73. [15] C. Gu, Soliton Theory and its Applications, Springer Science and Business Media, 2013. [16] A. Hasegawa, Y. Kodama and A. Maruta, Recent progress in dispersion-managed soliton transmission technologies, Optical Fiber Technology, 1997, 3(3), 197–213. doi: 10.1006/ofte.1997.0227 [17] J. H. He, Homotopy perturbation technique, Computer methods in applied mechanics and engineering, 1999,178(3–4), 257–262. doi: 10.1016/S0045-7825(99)00018-3 [18] B. Hong, Assorted exact explicit solutions for the generalized Atangana's fractional BBM-Burgers equation with the dissipative term, Frontiers in Physics, 2022, 10, 1152. [19] W. P. Hu, Z. C. Deng, S. M. Han and W. Fa, Multi-symplectic Runge-Kutta methods for Landau-Ginzburg-Higgs equation, Applied Mathematics and Mechanics, 2009, 30(8), 1027–1034. doi: 10.1007/s10483-009-0809-x [20] A. Iftikhar, A. Ghafoor, T. Zubair, S. Firdous and S. T. Mohyud-Din, Solutions of (2+1) dimensional generalized KdV, Sin Gordon and Landau-Ginzburg-Higgs Equations, Scientific Research and Essays, 2013, 8(28), 1349–1359. [21] M. E. Islam and M. A. Akbar, Stable wave solutions to the Landau-Ginzburg-Higgs equation and the modified equal width wave equation using the IBSEF method, Arab Journal of Basic and Applied Sciences, 2020, 27(1), 270–278. doi: 10.1080/25765299.2020.1791466 [22] A. Jhangeer, A. Hussain, M. Junaid-U-Rehman, D. Baleanu and M. B. Riaz, Quasi-periodic, chaotic and travelling wave structures of modified Gardner equation, Chaos, Solitons and Fractals, 2021,143, 110578. doi: 10.1016/j.chaos.2020.110578 [23] S. S. Kazmi, A. Jhangeer, N. Raza, H. I. Alrebdi, A. H. Abdel-Aty and H. Eleuch, The analysis of bifurcation, quasi-periodic and solitons patterns to the new form of the generalized q-deformed Sinh-Gordon equation, Symmetry, 2023, 15(7), 1324. doi: 10.3390/sym15071324 [24] Y. S. Kivshar and G. Agrawal, Optical Solitons: From Fibers to Photonic Crystals, Academic Press., 2003. [25] J. Li and F. Chen, Bifurcations and exact traveling wave solutions of degenerate coupled multi-KdV equations, International Journal of Bifurcation and Chaos, 2016, 26(03), 1650045. doi: 10.1142/S0218127416500450 [26] C. R. Qin and J. G. Liu, Study on double-periodic soliton and non-traveling wave solutions of integrable systems with variable coefficients, Results in Physics, 2022, 34, 105254. doi: 10.1016/j.rinp.2022.105254 [27] N. Raza, M. R. Aslam and H. Rezazadeh, Analytical study of resonant optical solitons with variable coefficients in Kerr and non-Kerr law media, Optical and Quantum Electronics, 2019, 51, 1–12. doi: 10.1007/s11082-018-1712-9 [28] N. Raza and S. S. Kazmi, Qualitative analysis and stationary optical patterns of nonlinear Schrödinger equation including nonlinear chromatic dispersion, Optical and Quantum Electronics, 2023, 55(8), 718. doi: 10.1007/s11082-023-04978-4 [29] H. Rezazadeh, M. Inc and D. Baleanu, New solitary wave solutions for variants of (3+1)-dimensional Wazwaz-Benjamin-Bona-Mahony equations, Frontiers in Physics, 2020, 8,332. doi: 10.3389/fphy.2020.00332 [30] A. Saha, Bifurcation, periodic and chaotic motions of the modified equal width-Burgers (MEW-Burgers) equation with external periodic perturbation, Nonlinear Dynamics, 2017, 87(4), 2193–2201. doi: 10.1007/s11071-016-3183-5 [31] F. Salman, N. Raza, G. A. Basendwah and M. M. Jaradat, Optical solitons and qualitative analysis of nonlinear Schrodinger equation in the presence of self steepening and self frequency shift, Results in Physics, 2022, 39, 105753. doi: 10.1016/j.rinp.2022.105753 [32] M. Senol, O. S. Iyiola, H. Daei Kasmaei and L. Akinyemi, Efficient analytical techniques for solving time-fractional nonlinear coupled Jaulent–Miodek system with energy-dependent Schrödinger potential, Advances in Difference Equations, 2019, 1–21. [33] L. Tang, Bifurcation analysis and multiple solitons in birefringent fibers with coupled Schrödinger-Hirota equation, Chaos, Solitons and Fractals, 2022,161, 112383. doi: 10.1016/j.chaos.2022.112383 [34] S. F. Tian, M. J. Xu and T. T. Zhang, A symmetry-preserving difference scheme and analytical solutions of a generalized higher-order beam equation, Proceedings of the Royal Society A, 2021,477(2255), 20210455. [35] A. M. Wazwaz, Multiple-soliton solutions for a (3+1)-dimensional generalized KP equation, Communications in Nonlinear Science and Numerical Simulation, 2012, 17(2), 491–495. [36] A. Zafar, M. Shakeel, A. Ali, L. Akinyemi and H. Rezazadeh, Optical solitons of nonlinear complex Ginzburg–Landau equation via two modified expansion schemes, Optical and Quantum Electronics, 2022, 54, 1–15. [37] E. M. Zayed, K. A. Gepreel, R. M. Shohib, M. E. Alngar and Y. Yildirim, Optical solitons for the perturbed Biswas-Milovic equation with Kudryashov's law of refractive index by the unified auxiliary equation method, Optik., 2021,230, 166286. [38] T. Y. Zhou, B. Tian, C. R. Zhang and S. H. Liu, Auto-Bäcklund transformations, bilinear forms, multiple-soliton, quasi-soliton and hybrid solutions of a (3+1)-dimensional modified Korteweg-de Vries-Zakharov-Kuznetsov equation in an electron-positron plasma, The European Physical Journal Plus, 2022,137(8), 912. [39] A. Zubair, N. Raza, M. Mirzazadeh, W. Liu and Q. Zhou, Analytic study on optical solitons in parity-time-symmetric mixed linear and nonlinear modulation lattices with non-Kerr nonlinearities, Optik., 2018,173,249–262. -
-
Figures(10)
Export File
Citation
Nauman Raza, Syeda Sarwat Kazmi, Ghada Ali Basendwah. DYNAMICAL ANALYSIS OF SOLITONIC, QUASI-PERIODIC, BIFURCATION AND CHAOTIC PATTERNS OF LANDAU-GINZBURG-HIGGS MODEL[J]. Journal of Applied Analysis & Computation, 2024, 14(1): 197-213. doi: 10.11948/20230137
Format
Content
DownLoad:
-
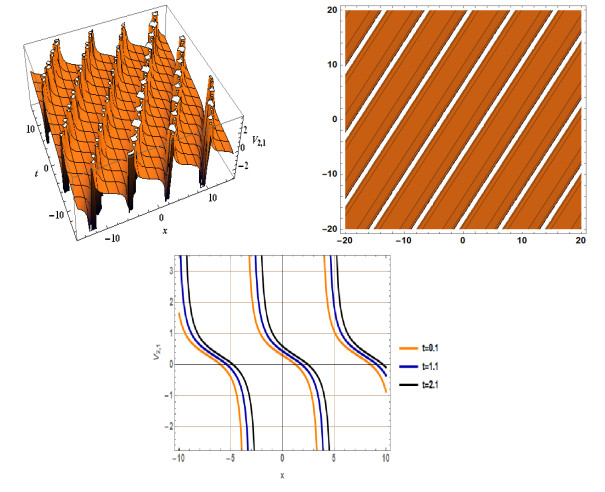
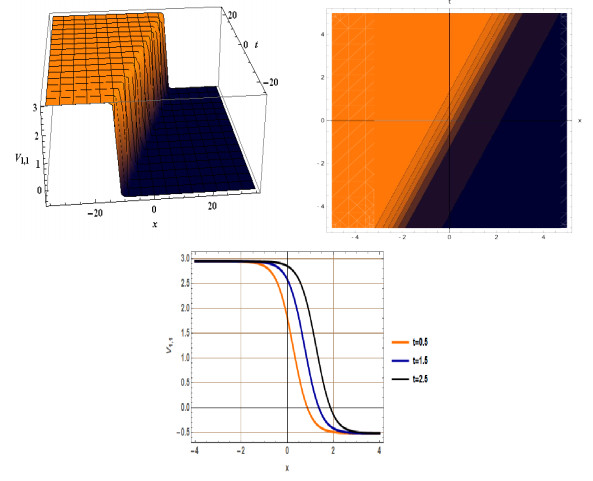
Figure 1.
3D, Contour and 2D plot for
$ V_{1,1}(x,t) $ $ \varrho= 2 $ $ \lambda =2 $ $ \vartheta = 0.5 $ $ b = 1 $ $ d=2.1 $ $ e=1 $ $ \mu=1 $ -
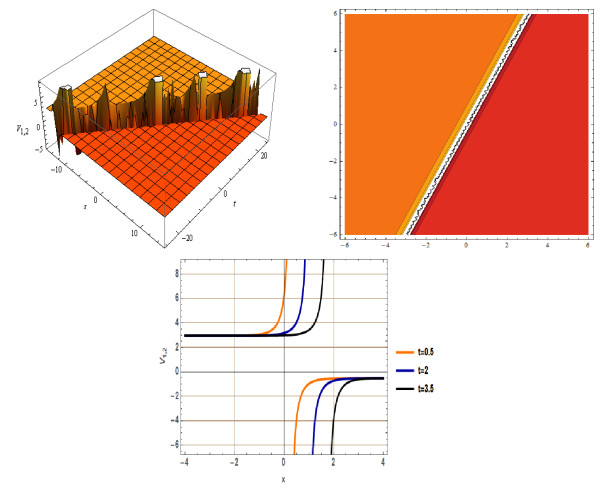
Figure 2.
3D, Contour and 2D plot for
$ V_{1,2}(x,t) $ $ \varrho= 2 $ $ \lambda =2 $ $ \vartheta = 0.5 $ $ b = 1 $ $ d=2.1 $ $ e=1 $ $ \mu=1 $ -
Figure 3.
3D, Contour and 2D plot for
$ V_{2,1}(x,t) $ $ \varrho= 1 $ $ \lambda =1 $ $ \vartheta = 1 $ $ b = 2 $ $ d=1 $ $ e=1 $ $ \mu=0.6 $ -
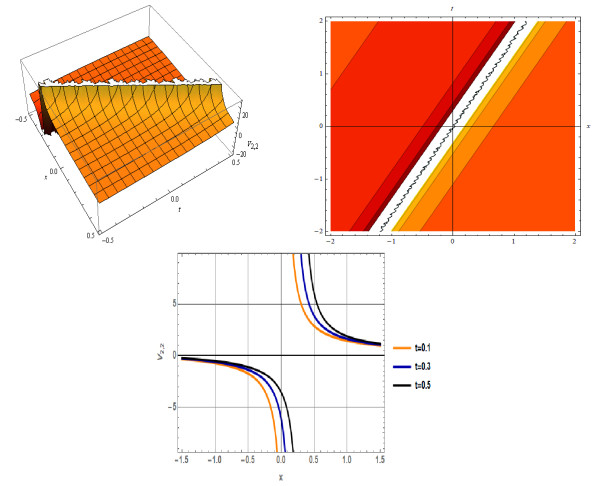
Figure 4.
3D, Contour and 2D plot for
$ V_{2,2}(x,t) $ $ \varrho= 1 $ $ \lambda =1 $ $ \vartheta = 1 $ $ b = 2 $ $ d=1 $ $ e=1 $ $ \mu=0.6 $ -
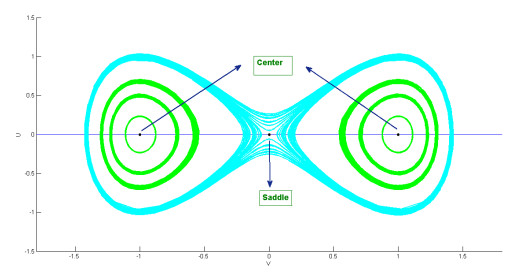
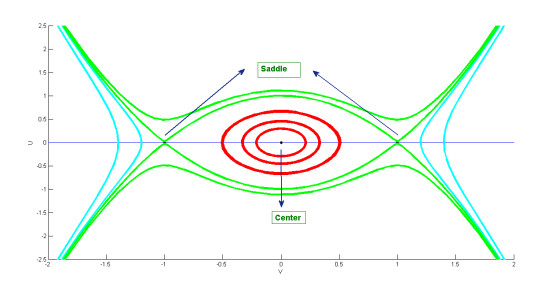
Figure 5.
Phase portrait for system (6.1), when
$ \zeta_1>0 $ $ \zeta_2>0 $ -
Figure 6.
Phase portrait for system (6.1), when
$ \zeta_1<0 $ $ \zeta_2<0 $ -
Figure 7.
For
$ \zeta_1=-3.2 $ $ \zeta_2 = 1.1 $ $ \delta_0 = 0.5 $ $ \omega =\pi $ -
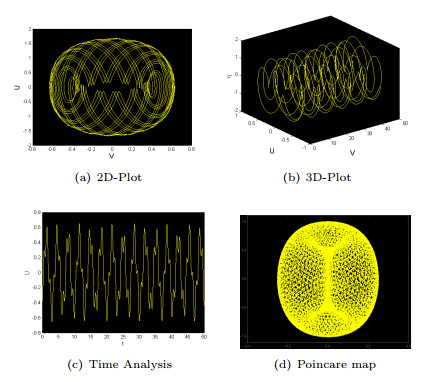
Figure 8.
For
$ \zeta_1=-3.2 $ $ \zeta_2 = 1.1 $ $ \delta_0 = 1.5 $ $ \omega =\pi $ -
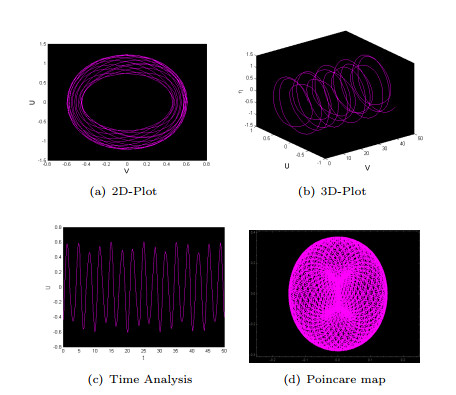
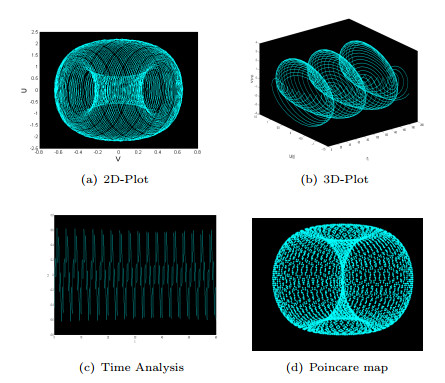
Figure 9.
For
$ \zeta_1=-3.2 $ $ \zeta_2 = 1.1 $ $ \delta_0 = 4.5 $ $ \omega =2\pi $ -
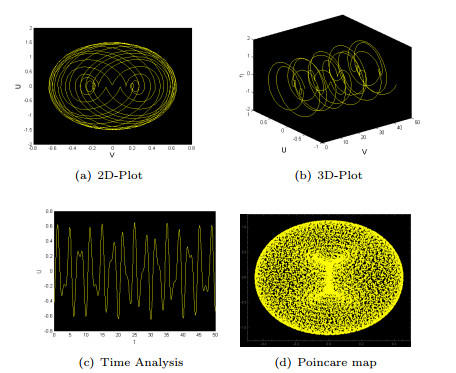
Figure 10.
For
$ \zeta_1=-3.2 $ $ \zeta_2 = 1.1 $ $ \delta_0 = 5.5 $ $ \omega =3\pi $