| Citation: | F. Afiatdoust, M. H. Heydari, M. M. Hosseini. BLOCK-BY-BLOCK TECHNIQUE FOR A CLASS OF NONLINEAR SYSTEMS OF FRACTIONAL INTEGRO-DIFFERENTIAL EQUATIONS[J]. Journal of Applied Analysis & Computation, 2024, 14(1): 214-234. doi: 10.11948/20230157 |
BLOCK-BY-BLOCK TECHNIQUE FOR A CLASS OF NONLINEAR SYSTEMS OF FRACTIONAL INTEGRO-DIFFERENTIAL EQUATIONS
-
Abstract
This work expresses an approximate approach for a class of nonlinear systems of fractional integro-differential equations. The proposed scheme uses the five-point Gauss-Lobatto quadrature method and the block-by-block technique. This procedure obtains automatically several approximate values of the problem at the same time. The analysis of convergence of the adopted approach is investigated. Moreover, it is proved that the convergence order of the method is $ O(h^8) $. Some numerical examples are considered to reveal the effectiveness of the method.
-

-
References
[1] A. A. Al-Marashi, Approximate solution of the system of linear fractional integro-differential equations of Volterra using b-spline method, J. Am. Res. Math. Stat, 2015, 3(2), 39–47. [2] A. Arikoglu and I. Ozkol, Solution of fractional integro-differential equations by using fractional differential transform method, Chaos, Solitons and Fractals, 2009, 40(2), 521–529. doi: 10.1016/j.chaos.2007.08.001 [3] M. Aslefallah and E. Shivanian, Nonlinear fractional integro-differential reaction-diffusion equation via radial basis functions, The European Physical Journal Plus, 2015,130(3), 1–9. [4] C. Canuto, M. Y. Hussaini, A. Quarteroni and T. A. Zang, Spectral Methods: Fundamentals in Single Domains, Springer Science and Business Media, 2007. [5] B. Cǎruntu, Approximate analytical solutions for systems of fractional nonlinear integro-differential equations using the polynomial least squares method, Fractal and Fractional, 2021, 5(4), 198. doi: 10.3390/fractalfract5040198 [6] S. A. Deif and S. R. Grace, Iterative refinement for a system of linear integro-differential equations of fractional type, Journal of Computational and Applied Mathematics, 2016,294,138–150. doi: 10.1016/j.cam.2015.08.008 [7] A. Ebadian and A. A. Khajehnasiri, Block-pulse functions and their applications to solving systems of higher-order nonlinear Volterra integro-differential equations, Electron. J. Differ. Equ, 2014, 54, 1–9. [8] A. A. Hamoud, K. Ghadle and S. Atshan, The approximate solutions of fractional integro-differential equations by using modified Adomian decomposition method, Khayyam Journal of Mathematics, 2019, 5(1), 21–39. [9] L. Huang, X. F. Li, Y. Zhao and X. Y. Duan, Approximate solution of fractional integro-differential equations by Taylor expansion method, Computers and Mathematics with Applications, 2011, 62(3), 1127–1134. doi: 10.1016/j.camwa.2011.03.037 [10] R. Katani and S. Shahmorad, Block by block method for the systems of nonlinear Volterra integral equations, Appl. Math. Model, 2010, 34,400–406. doi: 10.1016/j.apm.2009.04.013 [11] R. Katani and S. Shahmorad, The block-by-block method with Romberg quadrature for the solution of nonlinear Volterra integral equations on large intervals, Ukrainian Mathematical Journal, 2012, 64(7), 1050–1063. doi: 10.1007/s11253-012-0698-x [12] R. Katani and S. Shahmorad, A block by block method with Romberg quadrature for the system of Urysohn type Volterra integral equations, Computational and Applied Mathematics, 2012, 31(1), 191–203. doi: 10.1590/S1807-03022012000100010 [13] H. Khan, M. Arif, S. T. Mohyud-Din and S. Bushnaq, Numerical solutions to systems of fractional Voltera integro differential equations, using Chebyshev wavelet method, Journal of Taibah University for Science, 2018, 12(5), 584–591. doi: 10.1080/16583655.2018.1510149 [14] H. Li, J. Li, G. Hong, J. Dong and Y. Ning, Fractional-order model and experimental verification of granules-beam coupled vibration, Mechanical Systems and Signal Processing, 2023,200, 110536. doi: 10.1016/j.ymssp.2023.110536 [15] M. Li, Three classes of fractional oscillators, Symmetry, 2018, 10(2), 40. doi: 10.3390/sym10020040 [16] M. Li, Theory of Fractional Engineering Vibrations, volume 9, Walter de Gruyter GmbH and Co KG, 2021. [17] P. Linz, A method for solving nonlinear Volterra integral equations of the second kind, Mathematics of Computation, 1969, 23(107), 595–599. doi: 10.1090/S0025-5718-1969-0247794-7 [18] X. H. Ma and C. Huang, Numerical solution of fractional integro-differential equations by a hybrid collocation method, Applied Mathematics and Computation, 2013,219(12), 6750–6760. doi: 10.1016/j.amc.2012.12.072 [19] R. Metzler and J. Klafter, The restaurant at the end of the random walk: Recent developments in the description of anomalous transport by fractional dynamics, Journal of Physics A: Mathematical and General, 2004, 37(31), R161. doi: 10.1088/0305-4470/37/31/R01 [20] R. C. Mittal and R. Nigam, Solution of fractional integro-differential equations by Adomian decomposition method, International Journal of Applied Mathematics and Mechanics, 2008, 4(2), 87–94. [21] D. S. Mohammed, Numerical solution of fractional integro-differential equations by least squares method and shifted Chebyshev polynomial, Mathematical Problems in Engineering, 2014, 2014. [22] P. Mokhtary, Discrete Galerkin method for fractional integro-differential equations, Acta Mathematica Scientia, 2016, 36(2), 560–578. doi: 10.1016/S0252-9602(16)30021-2 [23] P. Mokhtary and F. Ghoreishi, The L2-convergence of the Legendre spectral tau matrix formulation for nonlinear fractional integro differential equations, Numerical Algorithms, 2011, 58(4), 475–496. doi: 10.1007/s11075-011-9465-6 [24] Y. Nawaz, Variational iteration method and homotopy perturbation method for fourth-order fractional integro-differential equations, Computers and Mathematics with Applications, 2011, 61(8), 2330–2341. doi: 10.1016/j.camwa.2010.10.004 [25] D. Nazari and S. Shahmorad, Application of the fractional differential transform method to fractional-order integro-differential equations with nonlocal boundary conditions, Journal of Computational and Applied Mathematics, 2010,234(3), 883–891. doi: 10.1016/j.cam.2010.01.053 [26] Y. Ordokhani and N. Rahimi, Numerical solution of fractional Volterra integro-differential equations via the rationalized Haar functions, J. Sci. Kharazmi Univ, 2014, 14(3), 211–224. [27] I. Podlubny, Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of their Solution and some of their Applications, Elsevier, 1998. [28] M. Richard, Fractional calculus in bioengineering, Critical ReviewsTM in Biomedical Engineering, 2004, 32(1), 1–377. doi: 10.1615/CritRevBiomedEng.v32.10 [29] J. Rouzegar, M. Vazirzadeh and M. H. Heydari, A fractional viscoelastic model for vibrational analysis of thin plate excited by supports movement, Mechanics Research Communications, 2020,110, 103618. doi: 10.1016/j.mechrescom.2020.103618 [30] H. Saeedi and M. M. Moghadam, Numerical solution of nonlinear Volterra integro-differential equations of arbitrary order by cas wavelets, Communications in Nonlinear Science and Numerical Simulation, 2011, 16(3), 1216–1226. doi: 10.1016/j.cnsns.2010.07.017 [31] P. K. Sahu and S. S. Ray, A new approach based on semi-orthogonal B-spline wavelets for the numerical solutions of the system of nonlinear Fredholm integral equations of second kind, Computational and Applied Mathematics, 2014, 33(3), 859–872. doi: 10.1007/s40314-013-0100-0 [32] P. K. Sahu and S. S. Ray, Legendre wavelets operational method for the numerical solutions of nonlinear Volterra integro-differential equations system, Applied Mathematics and Computation, 2015, (256), 715–723. [33] S. A. A. Saify, Numerical Methods for a System of Linear Volterra Integral Equations, 2005. [34] K. Sayevand, M. Fardi, E. Moradi and F. H. Boroujeni, Convergence analysis of homotopy perturbation method for Volterra integro-differential equations of fractional order, Alexandria Engineering Journal, 2013, 52(4), 807–812. doi: 10.1016/j.aej.2013.08.008 [35] L. Shen, S. Zhu, B. Liu, Z. Zhang and Y. Cui, Numerical implementation of nonlinear system of fractional Volterra integral-differential equations by Legendre wavelet method and error estimation, Numerical Methods for Partial Differential Equations, 2021, 37(2), 1344–1360. doi: 10.1002/num.22582 [36] C. C. Tisdell, On Picard's iteration method to solve differential equations and a pedagogical space for otherness, International Journal of Mathematical Education in Science andTechnology, 2019, 50(5), 788–799. [37] Y. Wang and L. Zhu, Solving nonlinear Volterra integro-differential equations of fractional order by using Euler wavelet method, Advances in difference equations, 2017, 2017(1), 1–16. doi: 10.1186/s13662-016-1057-2 [38] Y. Wang and L. Zhu, SCW method for solving the fractional integro-differential equations with a weakly singular kernel, Applied Mathematics and Computation, 2016,275, 72–80. doi: 10.1016/j.amc.2015.11.057 [39] J. Xie, Q. Huang and F. Zhao, Numerical solution of nonlinear Volterra-Fredholm-Hammerstein integral equations in two-dimensional spaces based on block pulse functions, Journal of Computational and Applied Mathematics, 2017,317,565–572. doi: 10.1016/j.cam.2016.12.028 [40] J. Xie and M. Yi, Numerical research of nonlinear system of fractional Volterra-Fredholm integral-differential equations via block-pulse functions and error analysis, Journal of Computational and Applied Mathematics, 2019,345,159–167. doi: 10.1016/j.cam.2018.06.008 [41] M. X. Yi, L. F. Wang and J. Huang, Legendre wavelets method for the numerical solution of fractional integro-differential equations with weakly singular kernel, Applied Mathematical Modelling, 2016, 40(4), 3422–3437. doi: 10.1016/j.apm.2015.10.009 [42] Y. Yin, Y. P. Chen and Y. Q. Huang, Convergence analysis of the Jacobi spectral-collocation method for fractional integro-differential equations, Acta Mathematica Scientia, 2014, 34(3), 673–690. doi: 10.1016/S0252-9602(14)60039-4 [43] A. Young, The application of approximate product-integration to the numerical solution of integral equations, Proceedings of the Royal Society of London. Series A, 1954, (224), 561–873. [44] H. A. Zedan, A. S. S. Tantawy and Y. M. Sayed, Convergence of the variational iteration method for initial-boundary value problem of fractional integro-differential equations, Journal of Fractional Calculus and Applications, 2014, 5(supplement 3), 1–14. [45] X. Zhang, B. Tang and Y. N. He, Homotopy analysis method for higher-order fractional integro-differential equations, Computers and Mathematics with Applications, 2011, 62(8), 3194–3203. doi: 10.1016/j.camwa.2011.08.032 [46] J. Zhao, J. Xiao and N. J. Ford, Collocation methods for fractional integro-differential equations with weakly singular kernels, Numerical Algorithms, 2014, 65(4), 723–743. doi: 10.1007/s11075-013-9710-2 -
-
-
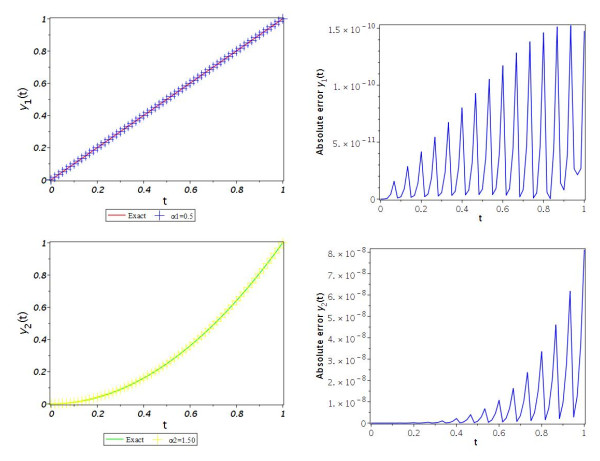
Figure 1.
Graphs of the true and approximate solutions (left), and associated absolute error functions (right) with
$ m=14 $ -
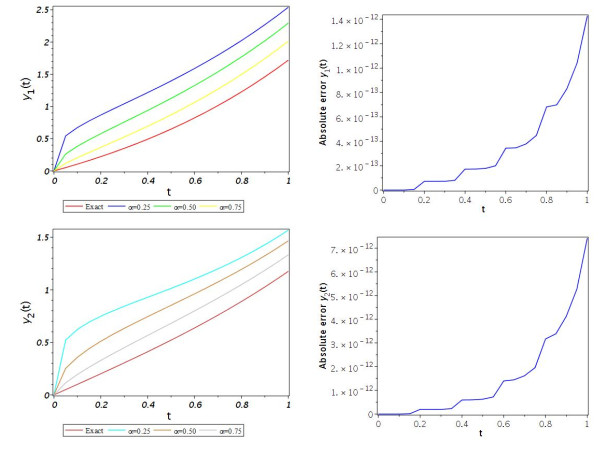
Figure 2.
Graphs of the true solution and approximate solutions with some values of
$ \alpha $ $ \alpha = 1 $ $ m=4 $ -
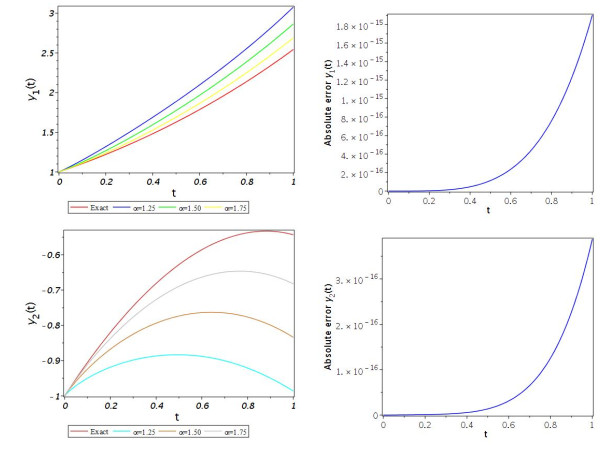
Figure 3.
Graphs of the true solution and approximate solutions with some values of
$ \alpha $ $ \alpha = 2 $ $ m=24 $ -
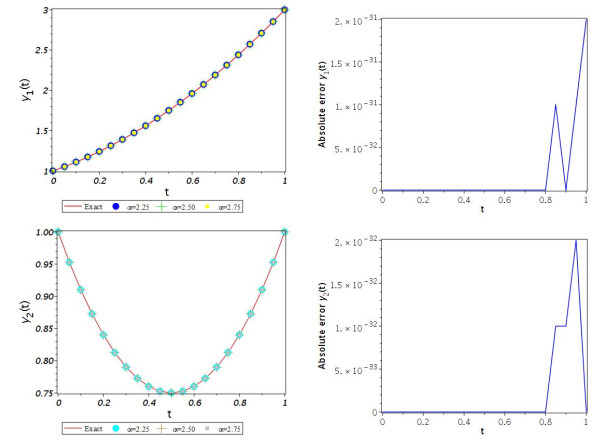
Figure 4.
Graphs of the true solution and approximate solutions with some values of
$ \alpha $ $ \alpha = 3 $ $ m=4 $ -
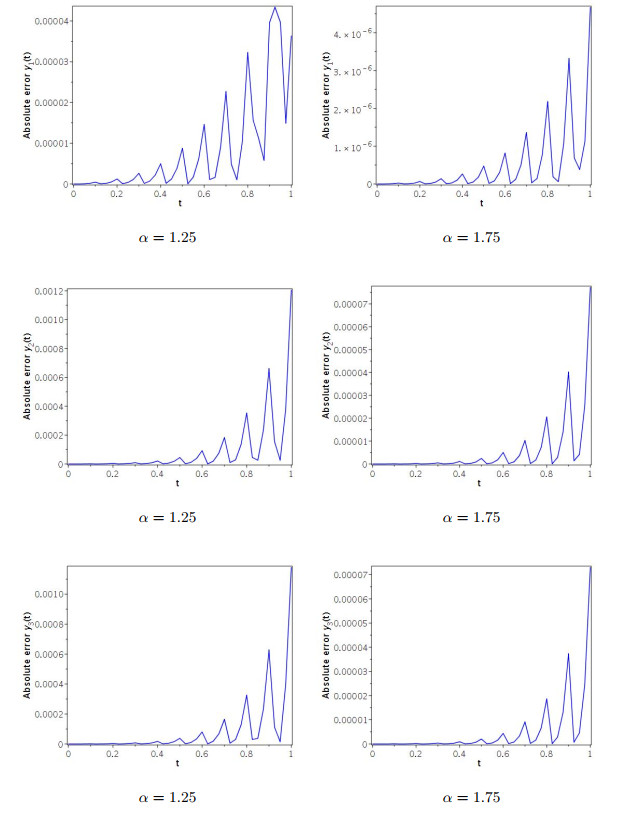
Figure 5.
Graphs of the absolute error functions for some values of
$ \alpha $ $ m=9 $




 DownLoad:
DownLoad: