| Citation: |
H. Dehestani, Y. Ordokhani, M. Razzaghi. EXECUTION OF A NOVEL DISCRETIZATION APPROACH FOR SOLVING VARIABLE-ORDER CAPUTO-RIESZ TIME-SPACE FRACTIONAL SCHRÖDINGER EQUATIONS[J]. Journal of Applied Analysis & Computation, 2024, 14(1): 235-262. doi: 10.11948/20230194
|
EXECUTION OF A NOVEL DISCRETIZATION APPROACH FOR SOLVING VARIABLE-ORDER CAPUTO-RIESZ TIME-SPACE FRACTIONAL SCHRÖDINGER EQUATIONS
-
Abstract
This work deals with the variable-order Caputo-Riesz (VO-CR) time-space fractional Schrödinger equations with the help of the Pell discretization method. For the first step, we separate the proposed problem into real and imaginary parts. Then, expanding the functions with respect to Pell polynomials and utilizing the required operational matrices. The operational matrices, together with the Pell discretization method, reduce the problem into a system of algebraic equations. It should be noted that the technique of obtaining the operational matrices strongly affects the precision of the numerical method process. Finally, we implement the proposed approach in several numerical experiments to confirm the theoretical scheme. And also, the comparison of obtained results with some existing methods is displayed in tables.
-
-
References
[1] J. B. Anderson, A random-walk simulation of the Schrodinger equation: $H^{+}_{3}$, J. Chem. Phys., 1975, 63(4), 1499–1503. doi: 10.1063/1.431514 [2] A. Babaei, B. P. Moghaddam, S. Banihashemi and J. A. T. Machado, Numerical solution of variable-order fractional integro-partial differential equations via Sinc collocation method based on single and double exponential transformations, Commun. Nonlinear Sci. Numer. Simul., 2020, 82, 104985. doi: 10.1016/j.cnsns.2019.104985 [3] A. H. Bhrawy, J. F. Alzaidy, M. A. Abdelkawy and A. Biswas, Jacobi spectral collocation approximation for multi-dimensional time-fractional Schrodinger equations, Nonlinear Dyn., 84(3), 2016, 1553–1567. doi: 10.1007/s11071-015-2588-x [4] A. H. Bhrawy and M. A. Zaky, Highly accurate numerical schemes for multi-dimensional space variable-order fractional Schrödinger equations, Comput. Math. Appl., 2017, 73(6), 1100–1117. doi: 10.1016/j.camwa.2016.11.019 [5] S. Cifani and E. R. Jakobsen, Entropy solution theory for fractional degenerate convection-diffusion equations, Ann. Inst. Henri Poincare, Anal. Non Lineaire, 2011, 28(3), 413–441. doi: 10.1016/j.anihpc.2011.02.006 [6] C. F. M. Coimbra, Mechanics with variable-order differential operators, Annals of Physics, 2003, 12,692–703. doi: 10.1002/andp.200351511-1203 [7] H. Dehestani and Y. Ordokhani, An efficient approach based on Legendre–Gauss–Lobatto quadrature and discrete shifted Hahn polynomials for solving Caputo–Fabrizio fractional Volterra partial integro-differential equations, J. Comput. Appl. Math., 2022,403, 113851. doi: 10.1016/j.cam.2021.113851 [8] H. Dehestani, and Y. Ordokhani, A spectral framework for the solution of fractional optimal control and variational problems involving Mittag–Leffler nonsingular kernel, J. Vib. Control, 2020, 1077546320974815. [9] H. Dehestani, Y. Ordokhani and M. Razzaghi, An improved numerical technique for distributed‐order time‐fractional diffusion equations, Numer. Methods Partial Differ. Equ., 2021, 37(3), 2490–2510. doi: 10.1002/num.22731 [10] H. Dehestani, Y. Ordokhani and M. Razzaghi, Fractional-order Legendre–Laguerre functions and their applications in fractional partial differential equations, Appl. Math. Comput., 2018,336,433–453, [11] R. P. Feynman and A. R. Hibbs, Quantum Mechanics and Path Integrals, McGraw-Hill, New York, 1965. [12] B. K. Ghimire, X. Li, C. S. Chen and A. R. Lamichhane, Hybrid Chebyshev polynomial scheme for solving elliptic partial differential equations, J. Comput. Appl. Math., 2020,364, 112324. doi: 10.1016/j.cam.2019.06.040 [13] M. H. Heydari and A. Atangana, A cardinal approach for nonlinear variable-order time fractional Schrödinger equation defined by Atangana–Baleanu–Caputo derivative, Chaos, Solitons & Fractals, 2019,128,339–348. [14] M. H. Heydari and M. Razzaghi, Jacobi spectral method for variable-order fractional Benney–Lin equation arising in falling film problems, J. Comput. Appl. Math., 2022,402, 113813. doi: 10.1016/j.cam.2021.113813 [15] B. Hicdurmaz, Finite difference schemes for time-fractional Schrödinger equations via fractional linear multistep method, Int. J. Comput. Math., 2021, 98(8), 1561–1573. doi: 10.1080/00207160.2020.1834088 [16] A. F. Horadam and J. M. Mahon, Pell and Pell-Lucas Polynomials, The Fibonacci Quarterly, 1985, 23(1), 7–20. [17] L. Hormander, The Analysis of Linear Partial Differential Operators, Springer, Berlin, 1990. [18] M. M. Khader and K. Saad, A numerical approach for solving the fractional Fisher equation using Chebyshev spectral collocation method, Chaos, Solitons & Fractals, 2018,110,169–177. [19] T. Koshy, Pell and Pell-Lucas Numbers with Applications, (Vol. 431). New York, Springer, 2014. [20] N. Laskin, Fractional quantum mechanics and Levy path integrals, Physics Letters A, 2000,268,298. doi: 10.1016/S0375-9601(00)00201-2 [21] N. Laskin, Fractional Schrödinger equation, Physical Review E, 2002, 66, 056108. doi: 10.1103/PhysRevE.66.056108 [22] N. Laskin, Fractals and quantum mechanics, Chaos, 2000, 10,780. doi: 10.1063/1.1050284 [23] J. G. Liu, M. S. Osman and A.M. Wazwaz, A variety of nonautonomous complex wave solutions for the (2+1)-dimensional non-linear Schrödinger equation with variable coefficients in non-linear optical fibers, Optik, 2019,180,917–923. doi: 10.1016/j.ijleo.2018.12.002 [24] J. G. Liu, M. S. Osman, W. H. Zhu, L. Zhou and G. P. Ai, Different complex wave structures described by the Hirota equation with variable coefficients in inhomogeneous optical fibers, Appl. Phys. B, 2019,125,175. [25] Q. Liu, F. Zeng and C. Li, Finite difference method for time-space-fractional Schrödinger equation, Int. J. Comput. Math., 2015, 92(7), 1439–1451. doi: 10.1080/00207160.2014.945440 [26] Z. Liu, S. Lu and F. Liu, Fully discrete spectral methods for solving time fractional nonlinear Sine–Gordon equation with smooth and non-smooth solutions, Appl. Math. Comput., 2018,333,213–224. [27] R. L. Magin, C. Ingo, L. Colon-Perez, W. Triplett and T. H. Mareci, Characterization of anomalous diffusion in porous biological tissues using fractional order derivatives and entropy, Microporous Mesoporous Mater, 2013,178, 39–43. doi: 10.1016/j.micromeso.2013.02.054 [28] B. Mathieu, P. Melchior, A. Oustaloup and C. Ceyral, Fractional differentiation for edge detection, Signal Process., 2003, 83(11), 2421–2432. doi: 10.1016/S0165-1684(03)00194-4 [29] I. Podlubny, Fractional Differential Equations, Academic Press, New York, 1999. [30] S. G. Samko, A. A. Kilbas and O. I. Marichev, Fractional Integrals and Derivatives: Theory and Applications, Gordon and Breach, Amsterdam, Translation from the Russian, 1993. [31] M. A. Sarhan, S. Shihab, B. E. Kashem and M. Rasheed, New Exact Operational Shifted Pell Matrices and Their Application in Astrophysics, in Journal of Physics: Conference Series (Vol. 1879, No. 2, p. 022122). IOP Publishing, 2021. [32] M. A. Sarhan, S. Shihab and M. Rasheed, A novel spectral modified Pell polynomials for solving singular differential equations, Al-Mustansiriyah Journal of Science, 2021, 32(1), 18–24. doi: 10.23851/mjs.v32i1.930 [33] M. A. Sarhan, S. Shihab and M. Rasheed, Some Results on a Two Variables Pell Polynomials, Al-Qadisiyah Journal of Pure Science, 2021, 26(1), 55–70. doi: 10.29350/qjps.2021.26.1.1246 [34] H. Singh, F. Akhavan Ghassabzadeh, E. Tohidi and C. Cattani, Legendre spectral method for the fractional Bratu problem, Math. Methods Appl. Sci., 2020, 43(9), 5941–5952. doi: 10.1002/mma.6334 [35] Y. Tasyurdu, D. Cifci and O. Deveci, Applications of Pell polynomials in rings, J. Math. Res., 2018, 10(3). [36] J. Wang, X. Liu and Y. Zhou, A high-order accurate wavelet method for solving Schrödinger equations with general nonlinearity, Appl. Math. Mech., 2018, 39(2), 275–290. doi: 10.1007/s10483-018-2299-6 [37] Y. Wang and L. Mei, A conservative spectral Galerkin method for the coupled nonlinear space-fractional Schrödinger equations, Int. J. Comput. Math., 2019, 96(12), 2387–2410. doi: 10.1080/00207160.2018.1563687 [38] S. Zhang and H. Q. Zhang, Fractional sub-equation method and its applications to nonlinear fractional PDEs, Phys. Lett. A, 2011,375(7), 1069–1073. doi: 10.1016/j.physleta.2011.01.029 [39] Y. Zhang, A. Kumar, S. Kumar, D. Baleanu and X. J. Yang, Residual power series method for time-fractional Schrödinger equations, J. Nonlinear Sci. Appl., 2016, 9(11), 5821–5829. doi: 10.22436/jnsa.009.11.10 [40] M. Zheng, F. Liu and Z. Jin, The global analysis on the spectral collocation method for time fractional Schrodinger equation, Appl. Math. Comput., 2020,365, 124689. -
-
Figures(7) / Tables(8)
Export File
Citation
H. Dehestani, Y. Ordokhani, M. Razzaghi. EXECUTION OF A NOVEL DISCRETIZATION APPROACH FOR SOLVING VARIABLE-ORDER CAPUTO-RIESZ TIME-SPACE FRACTIONAL SCHRÖDINGER EQUATIONS[J]. Journal of Applied Analysis & Computation, 2024, 14(1): 235-262. doi: 10.11948/20230194
Format
Content
DownLoad:
-
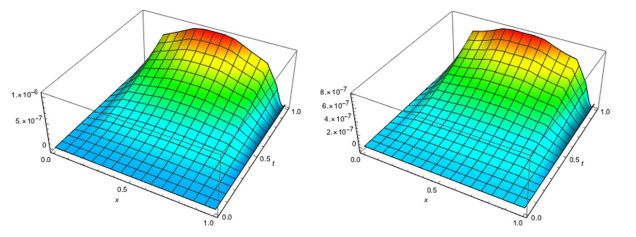
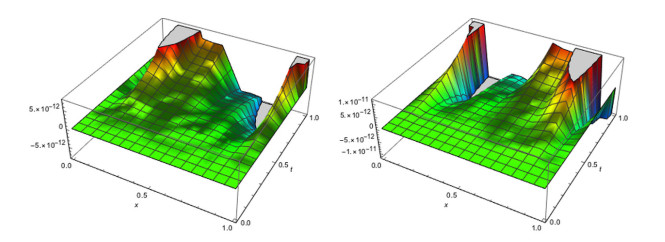
Figure 1.
The absolute error of the real part (left) and imaginary part of the approximate solution (right) obtained with
$ \alpha(x,t)=0.2,\beta=1.8 $ $ M=N=3 $ -
Figure 2.
The absolute error of the real part (left) and imaginary part of the approximate solution (right) obtained with
$ \alpha(x,t)=0.2,\beta=1.8 $ $ M=3,N=7 $ -
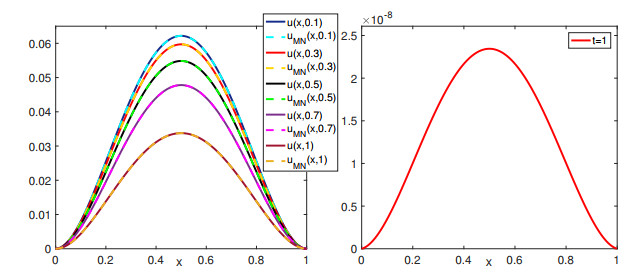
Figure 3.
The approximation of the real part at different time (left) and absolute error of real part at
$ t=1 $ $ \alpha(x,t)=0.5 $ $ M=4,N=5 $ -
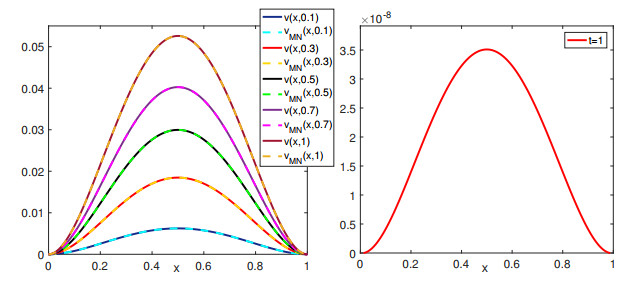
Figure 4.
The approximation of the imaginary part at different time (left) and absolute error of imaginary part at
$ t=1 $ $ \alpha(x,t)=0.5 $ $ M=4,N=5 $ -
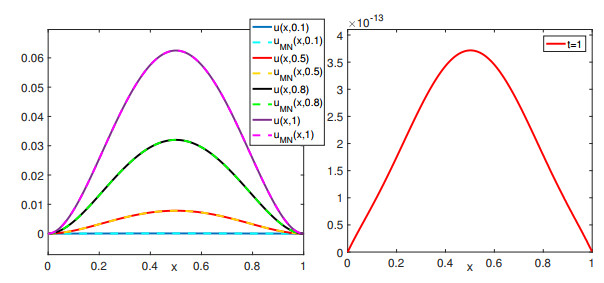
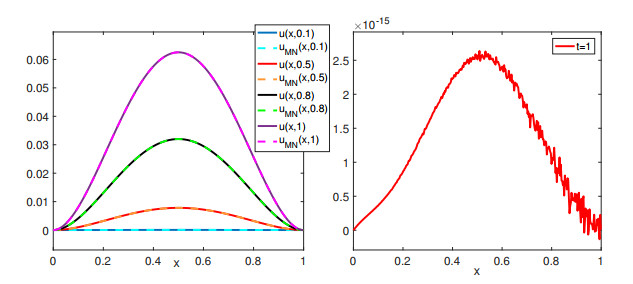
Figure 5.
The approximation at different time (left) and absolute error at
$ t=1 $ $ \alpha(x,t)=0.5, $ $ \beta=1.5 $ $ M=4,N=5 $ -
Figure 6.
The approximation at different time (left) and absolute error at
$ t=1 $ $ \alpha(x,t)=\frac{2+\sin(xt)}{400}, $ $ \beta=1.5 $ $ M=4,N=5 $ -
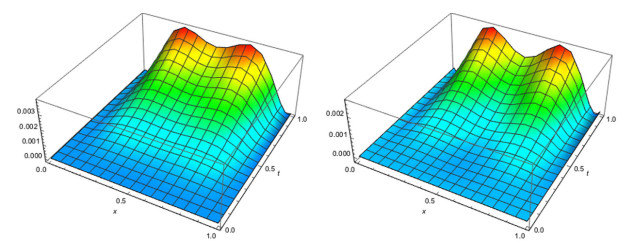
Figure 7.
The absolute error of the real part (left) and imaginary part (right) of approximate solution obtained with
$ \alpha(x,t)=0.75+0.2\exp(-xt) $ $ M=6,N=3 $