| Citation: | Mohamed M. Khader, Ali H. Tedjani. NUMERICAL SIMULATION FOR THE FRACTIONAL-ORDER SMOKING MODEL USING A SPECTRAL COLLOCATION METHOD BASED ON THE GEGENBAUER WAVELET POLYNOMIALS[J]. Journal of Applied Analysis & Computation, 2024, 14(2): 847-863. doi: 10.11948/20230178 |
NUMERICAL SIMULATION FOR THE FRACTIONAL-ORDER SMOKING MODEL USING A SPECTRAL COLLOCATION METHOD BASED ON THE GEGENBAUER WAVELET POLYNOMIALS
-
Abstract
Smoking is a social trend that is prevalent around the world, particularly in places of learning and at some significant events. The World Health Organization (WHO) defines smoking as the most important preventable cause of disease and the third major cause of death in humans. So, in this paper, we present an effective simulation to study the solution behavior of the Liouville-Caputo fractional-order smoking model by using a presumably new approximation technique that is based on the Gegenbauer wavelet polynomials (GWPs). We use the spectral collocation method based on the properties of GWPs. This procedure converts the given model into a system of algebraic equations. We satisfy the efficiency and accuracy of the given procedure by evaluating the residual error function. The results obtained are then compared with the results obtained by using the fourth-order Runge-Kutta method. Our results show that the implemented technique provides an easy and efficient tool to simulate the solution of such smoking models.
-

-
References
[1] M. Adel, H. M. Srivastava and M. M. Khader, Implementation of an accurate method for the analysis and simulation of electrical R-L circuits, Mathematical Methods in the Applied Sciences, 2022, 12, 1–10. [2] Z. Alkhudhari, S. Al-Sheikh and S. Al-Tuwairqi, Global dynamics of a mathematical model on smoking, Applied Mathematics, 2014, 847075, 1–16. [3] Y. N. Anjam, R. Shafqat, I. E. Sarris, M. Rahma, S. Touseef and M. Arshad, A fractional order investigation of smoking model using Caputo-Fabrizio differential operator, Fractal and Fractional, 2022, 6, 1–18. [4] I. Celik, Gegenbauer wavelet collocation method for the extended Fisher-Kolmogorov equation in two dimensions, Mathematical Methods in the Applied Sciences, 2020, 43, 5615–5628. doi: 10.1002/mma.6300 [5] I. Celik, Generalization of Gegenbauer wavelet collocation method to the generalized Kuramoto-Sivashinsky equation, International Journal of Applied and Computational Mathematics, 2018, 13, 4–11. [6] H. M. El-Hawary, M. S. Salim and H. S. Hussien, Ultraspherical integral method for optimal control problems governed by ordinary differential equations, Journal of Global Optimization, 2003, 25(3), 283–303. doi: 10.1023/A:1022463810376 [7] V. S. Ertürk, G. Zaman and S. Momani, A numeric analytic method for approximating a giving up smoking model containing fractional derivatives, Computational & Applied Mathematics, 2012, 64, 3068–3074. [8] C. C. Garsow, G. J. Salivia and A. R. Herrera, Mathematical Models for Dynamics of Tobacco Use, Recovery and Relapse, Technical Report Series BU-1505-M; Cornell University: London, UK, 2000. [9] I. Goldenberg, M. Jonas, A. Tenenbaum, V. Boyko, S. Matetzky, A. Shotan, S. Behar and H. R. Reiss, Current smoking, smoking cessation, and the risk of sudden cardiac death in patients with coronary artery disease, Archives of Internal Medicine, 2003, 163, 2301–2305. doi: 10.1001/archinte.163.19.2301 [10] A. R. Hadhoud, H. M. Srivastava and A. A. M. Rageh, Non-polynomial B-spline and shifted Jacobi spectral collocation techniques to solve time-fractional nonlinear coupled Burgers' equations numerically, Advances in Difference Equations, 2021, 439, 1–28. [11] O. K. Ham, Stages and processes of smoking cessation among adolescents, Western Journal of Nursing Research, 2007, 29, 301–315. doi: 10.1177/0193945906295528 [12] Y. F. Ibrahim, M. M. Khader, A. Megahed, F. Abd Elsalam and M. Adel, An efficient numerical simulation for the fractional COVID-19 model by using the GRK4M together and the fractional FDM, Fractal and Fractional, 2022, 6, 1–14. [13] M. A. Iqbal, M. Shakeel, S. T. Mohyud-Din and M. Rafiq, Modified wavelets-based algorithm for nonlinear delay differential equations of fractional order, Advances in Mechanical Engineering, 2017, 9(4), 1–8. [14] M. M. Khader and K. M. Abualnaja, Galerkin-FEM for obtaining the numerical solution of the linear fractional Klein-Gordon equation, Journal of Applied Analysis and Computation, 2019, 9, 261–270. [15] M. M. Khader and M. Adel, Numerical approach for solving the Riccati and Logistic equations via QLM-rational Legendre collocation method, Computational and Applied Mathematics, 2020, 39, 1–9. doi: 10.1007/s40314-019-0964-8 [16] M. M. Khader and M. Adel, Modeling and numerical simulation for covering the fractional COVID-19 model using spectral collocation-optimization algorithms, Fractal and Fractional, 2022, 6, 1–19. [17] S. Kumar, R. K. Pandey, H. M. Srivastava and G. N. Singh, A convergent collocation approach for generalized fractional integro-differential equations using Jacobi poly-fractonomials, Mathematics, 2021, 9, 1–17. [18] M. M. Khader and K. M. Saad, A numerical study using Chebyshev collocation method for a problem of biological invasion: Fractional Fisher equation, International Journal of Biomathematics, 2018, 11, 1–15. [19] M. M. Khader and R. P. Sharma, Evaluating the unsteady MHD micropolar fluid flow past stretching/shirking sheet with heat source and thermal radiation: Implementing fourth order predictor-corrector FDM, Mathematics and Computers in Simulation, 2021, 181, 333–350. doi: 10.1016/j.matcom.2020.09.014 [20] T. Liu, T. J. Deiss, M. W. Lippi, A. Jauregui, K. Vessel, S. Ke, A. Belzer, H. Zhuo, K. N. Kangelaris, A. D. Gomez, M. A. Matthay, K. D. Liu and C. S. Calfee, Alternative tobacco product use in critically ill patients, International Journal of Environmental Research and Public Health, 2020, 17, 1–15. [21] N. Ozdemir, A. Secer and M. Bayram, The Gegenbauer wavelets-based computational methods for the coupled system of Burgers' equations with time-fractional derivative, Mathematics, 2019, 7, 1–15. [22] M. U. Rehman and U. Saeed, Gegenbauer wavelets operational matrix method for fractional differential equations, Journal of the Korean Mathematical Society, 2015, 52, 1069–1096. [23] K. M. Saad, M. M. Khader, J. F. Gomez-Aguilar and D. Baleanu, Numerical solutions of the fractional Fisher's type equations with Atangana-Baleanu fractional derivative by using spectral collocation methods, Chaos, 2019, 29, 1–5. [24] A. Saadatmandi and M. Dehghan, A new operational matrix for solving fractional-order differential equations, Computers & Mathematics with Applications, 2010, 59, 1326–1336. [25] A. Secer and N. Ozdemir, An effective computational approach based on Gegenbauer wavelets for solving the time-fractional Kdv-Burgers-Kuramoto equation, Advances in Difference Equations, 2019, 389–393. [26] K. Shah, M. Sinan, T. Abdeljawad, M. A. El-Shorbagy, B. Abdalla and M. S. Abualrub, A Detailed study of a fractal-fractional transmission dynamical model of viral infectious disease with vaccination, Complexity, 2022, 7236824, 1–21. [27] A. M. Shloof, A. Ahmadian, N. Senu, S. Salahshour, S. N. I. Ibrahim and M. Pakdaman, A highly accurate artificial neural networks scheme for solving higher multi-order fractal-fractional differential equations based on generalized Caputo derivative, 2023, 124, 4371–4404. [28] A. M. Shloof, N. Senu, A. Ahmadian, N. M. A. B. N. Long and S. Salahshour, Solving fractal-fractional differential equations using an operational matrix of derivatives via Hilfer fractal-fractional derivative sense, Applied Numerical Mathematics, 2022, 178(2), 386–403. [29] A. M. Shloof, N. Senu, A. Ahmadian and S. Salahshour, An efficient operation matrix method for solving fractal-fractional differential equations with generalized Caputo-type fractional-fractal derivative, Mathematics and Computers in Simulation, 2021, 188, 415–435. [30] H. M. Srivastava, Some parametric and argument variations of the operators of fractional calculus and related special functions and integral transformations, Journal of Nonlinear and Convex Analysis, 2021, 22, 1501–1520. [31] H. M. Srivastava, F. A. Shah and R. Abass, An application of the Gegenbauer wavelet method for the numerical solution of the fractional Bagley-Torvik equation, Russian Journal of Mathematical Physics, 2019, 26, 77–93. [32] M. Usman, M. Hamid, R. U. Haq and W. Wang, An efficient algorithm based on Gegenbauer wavelets for the solutions of variable-order fractional differential equations, The European Physical Journal Plus, 2018, 13, 133–150. [33] World Health Organization, Monitoring Tobacco Use and Prevention Policies, Executive Summary, World Health Organization: Geneva, Switzerland, 2017. [34] A. Yildirum and Y. Cherruault, Analytical approximate solution of a SIR epidemic model with constant vaccination strategy by homotopy perturbation method, Emerald, 2009, 38, 1566–1581. [35] A. Zeb, I. Chohan and G. Zaman, The homotopy analysis method for approximating of giving up smoking model in fractional order, Applied Mathematics, 2012, 3, 914–919. -
-
-
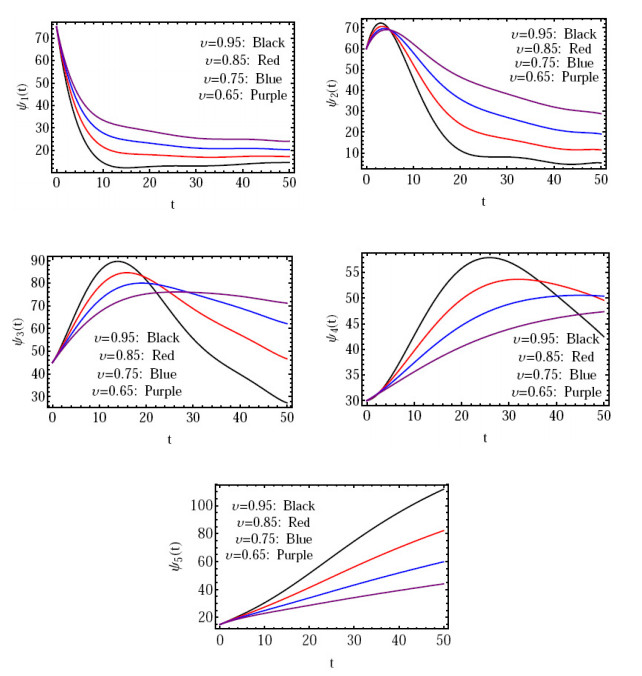
Figure 1.
The approximate solution
$ \psi_{i}(t), \, i=1(1)5 $ $ \nu $ -
Figure 2.
The approximate solution
$ \psi_{i}(t), \, i=1(1)5 $ $ \nu $ -
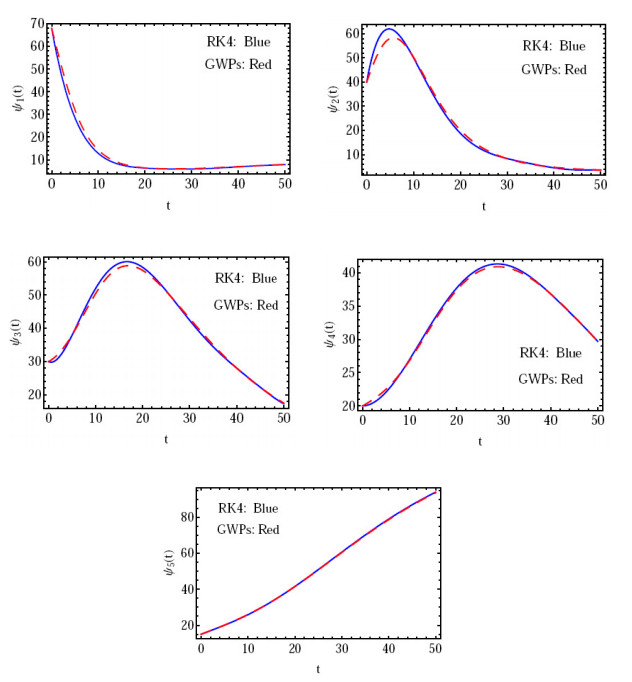
Figure 3.
The solution
$ \psi_{i}(t), \, i=1(1)5 $ $ \nu=1 $ -
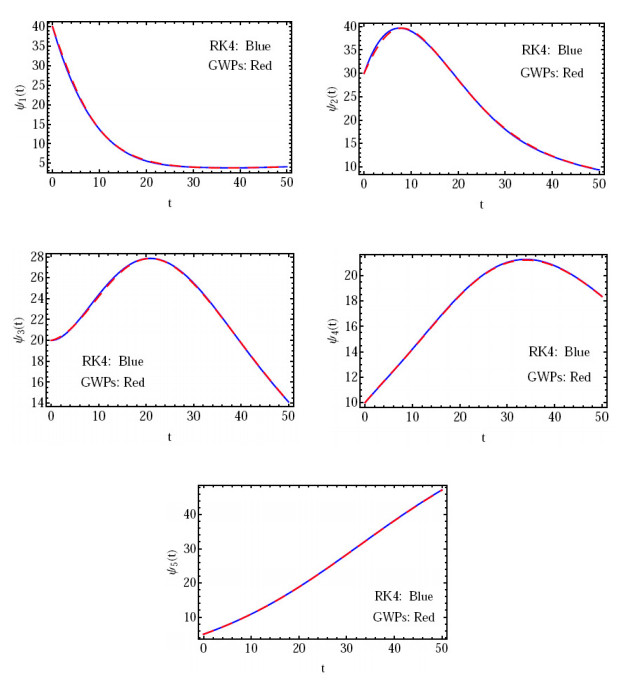
Figure 4.
The solution
$ \psi_{i}(t), \, i=1(1)5 $ $ \nu=1 $ -
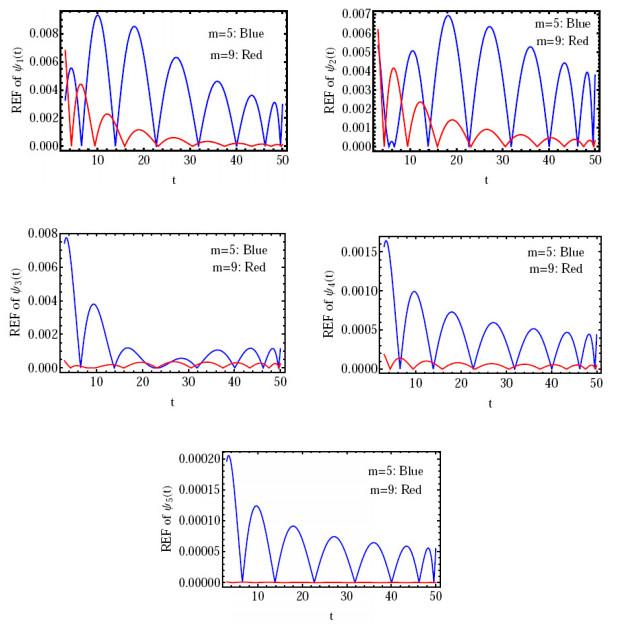
Figure 5.
The REF of
$ \psi_{i}(t), \, i=1(1)5 $ $ m $ -
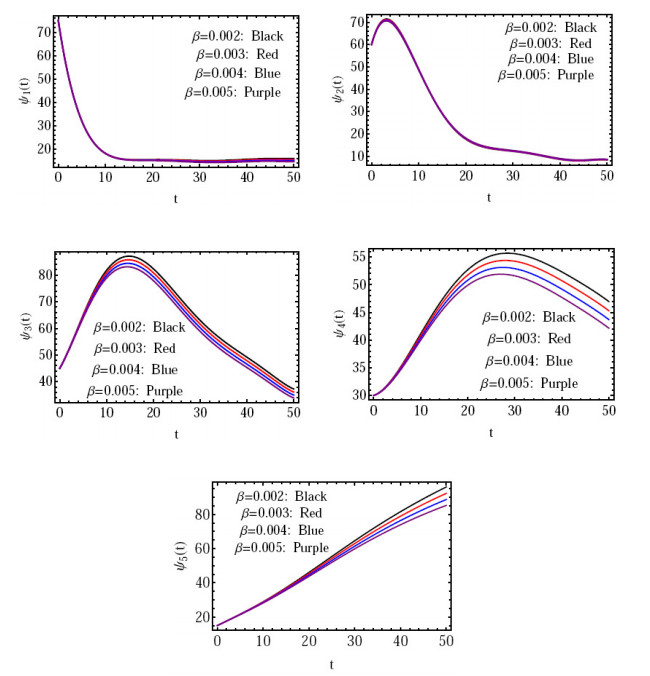
Figure 6.
The effect of
$ \beta $ $ \psi_{i}(t), \, i=1(1)5 $





 DownLoad:
DownLoad: