| Citation: | Zohreh Eskandari, Parvaiz Ahmad Naik, Mehmet Yavuz. DYNAMICAL BEHAVIORS OF A DISCRETE-TIME PREY-PREDATOR MODEL WITH HARVESTING EFFECT ON THE PREDATOR[J]. Journal of Applied Analysis & Computation, 2024, 14(1): 283-297. doi: 10.11948/20230212 |
DYNAMICAL BEHAVIORS OF A DISCRETE-TIME PREY-PREDATOR MODEL WITH HARVESTING EFFECT ON THE PREDATOR
-
Abstract
This study investigates the dynamics of a discrete-time prey-predator model with a harvesting effect on the predator. During the analysis of the bifurcations at the interior fixed point, we find that there are some generic bifurcations, including fold, flip, Neimark-Sacker, and strong resonance bifurcations. Using the normal form theory and the center manifold theorem, we can characterize these bifurcations. Furthermore, we determine the non-degeneracy conditions for the computed bifurcations and compute the critical normal form coefficients. Our analysis of the obtained analytical results as well as the revealing of more complex dynamical behaviors that cannot be achieved analytically is carried out using the numerical continuation method by computing several bifurcation curves emanating from the detected bifurcation points.
-

-
References
[1] S. Chakraborty, S. Pal and N. Bairagi, Predator-prey interaction with harvesting: Mathematical study with biological ramifications, Applied Mathematical Modelling, 2012, 36(9), 4044–4059. doi: 10.1016/j.apm.2011.11.029 [2] Z. Eskandari, J. Alidousti, Z. Avazzadeh and J. T. Machado, Dynamics and bifurcations of a discrete-time prey-predator model with Allee effect on the prey population, Ecological Complexity, 2021, 48, 100962. doi: 10.1016/j.ecocom.2021.100962 [3] Z. Eskandari, Z. Avazzadeh and R. K. Ghaziani, Theoretical and numerical bifurcation analysis of a predator-prey system with ratio-dependence, Mathematical Sciences, 2023, 18, 1–12. [4] Z. Eskandari, Z. Avazzadeh, R. K. Ghaziani and B. Li, Dynamics and bifurcations of a discrete-time Lotka-Volterra model using nonstandard finite difference discretization method, Mathematical Methods in the Applied Sciences, 2022, 46(7), 7045–7059. [5] Z. Eskandari, R. K. Ghaziani and Z. Avazzadeh, Bifurcations of a discrete-time SIR epidemic model with logistic growth of the susceptible individuals, International Journal of Biomathematics, 2023, 16(6), 2250120. doi: 10.1142/S1793524522501200 [6] M. Farman, M. F. Tabassum, P. A. Naik and S. Akram, Numerical treatment of a nonlinear dynamical hepatitis B model: An evolutionary approach, The European Physical Journal Plus, 2020, 135 (12), 941. doi: 10.1140/epjp/s13360-020-00902-x [7] H. I. Freedman, Deterministic Mathematical Models in Population Ecology, Marcel Dekker Incorporated, 57, 1980. [8] X. Gao, S. Ishag, S. Fu, W. Li and W. Wang, Bifurcation and turing pattern formation in a diffusive ratio-dependent predator-prey model with predator harvesting, Nonlinear Analysis: Real World Applications, 2020, 51, 102962. doi: 10.1016/j.nonrwa.2019.102962 [9] M. Gholami, R. K. Ghaziani and Z. Eskandari, Three-dimensional fractional system with the stability condition and chaos control, Mathematical Modeling and Numerical Simulation with Applications, 2022, 2(1), 41–47. doi: 10.53391/mmnsa.2022.01.004 [10] M. B. Ghori, Y. Kang Y. Chen, Emergence of stochastic resonance in a two-compartment hippocampal pyramidal neuron model, Journal of Computational Neuroscience, 2022, 50(2), 217–240. doi: 10.1007/s10827-021-00808-2 [11] M. B. Ghori, P. A. Naik, J. Zu, Z. Eskandari and M. Naik, Global dynamics and bifurcation analysis of a fractional-order SEIR epidemic model with saturation incidence rate, Mathematical Methods in the Applied Sciences, 2022, 45(7), 3665–3688. doi: 10.1002/mma.8010 [12] W. Govaerts, R. K. Ghaziani, Y. A. Kuznetsov and H. G. Meijer, Numerical methods for two-parameter local bifurcation analysis of maps, SIAM Journal on Scientific Computing, 2007, 29(6), 2644–2667. doi: 10.1137/060653858 [13] J. Guckenheimer and P. Holmes, Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields, Springer Science & Business Media, 42, 2013. [14] Z. He and X. Lai, Bifurcation and chaotic behavior of a discrete-time predator-prey system, Nonlinear Analysis: Real World Applications, 2011, 12(1), 403–417. doi: 10.1016/j.nonrwa.2010.06.026 [15] C. M. Heggerud and K. Lan, Local stability analysis of ratio-dependent predator-prey models with predator harvesting rates, Applied Mathematics and Computation, 2015, 270, 349–357. doi: 10.1016/j.amc.2015.08.062 [16] C. S. Holling, The functional response of predators to prey density and its role in mimicry and population regulation, The Memoirs of the Entomological Society of Canada, 1965, 97(S45), 5–60. doi: 10.4039/entm9745fv [17] S. R. J. Jang, Allee effects in a discrete-time host-parasitoid model, Journal of Difference Equations and Applications, 2006, 12(2), 165–181. doi: 10.1080/10236190500539238 [18] S. R. J. Jang, Discrete-time host-parasitoid models with Allee effects: Density dependence versus parasitism, Journal of Difference Equations and Applications, 2011, 17(04), 525–539. doi: 10.1080/10236190903146920 [19] H. Joshi, M. Yavuz and I. Stamova, Analysis of the disturbance effect in intracellular calcium dynamic on fibroblast cells with an exponential kernel law, Bulletin of Biomathematics, 2023, 1(1), 24–39. [20] L. E. Keshet, Mathematical models in biology, SIAM, 2005, 1–586. [21] Y. A. Kuznetsov, Elements of Applied Bifurcation Theory, Springer Science & Business Media, 112, 2013. [22] Y. A. Kuznetsov and H. G. Meijer, Numerical normal forms for codim 2 bifurcations of fixed points with at most two critical eigenvalues, SIAM Journal on Scientific Computing, 2005, 26(6), 1932–1954. doi: 10.1137/030601508 [23] Y. A. Kuznetsov and H. G. Meijer, Numerical Bifurcation Analysis of Maps: From Theory to Software, Cambridge University Press, 2019. [24] X. Liu and D. Xiao, Bifurcations in a discrete time Lotka-Volterra predator-prey system, Discrete and Continuous Dynamical Systems-B, 2006, 6(3), 559–572. doi: 10.3934/dcdsb.2006.6.559 [25] G. Livadiotis, L. Assas, B. Dennis, S. Elaydi and E. Kwessi, A discrete-time host-parasitoid model with an Allee effect, Journal of Biological Dynamics, 2015, 9(1), 34–51. doi: 10.1080/17513758.2014.982219 [26] A. J. Lotka, Elements of physical biology, Nature, 1925, 116, 461. [27] V. Madhusudanan, K. Anitha, S. Vijaya and M. Gunasekaran, Complex effects in discrete time prey-predator model with harvesting on prey, The International Journal of Engineering and Science, 2014, 3(4), 1–5. [28] P. A. Naik and Z. Eskandari, Nonlinear dynamics of a three-dimensional discrete-time delay neural network, International Journal of Biomathematics, 2024, 17(4), 2350057. [29] P. A. Naik, Z. Eskandari, Z. Avazzadeh and J. Zu, Multiple bifurcations of a discrete-time prey-predator model with mixed functional response, International Journal of Bifurcation and Chaos, 2022, 32(04), 2250050. doi: 10.1142/S021812742250050X [30] P. A. Naik, Z. Eskandari, A. Madzvamuse, Z. Avazzadeh and J. Zu, Complex dynamics of a discrete-time seasonally forced SIR epidemic model, Mathematical Methods in the Applied Sciences, 2023, 46(6), 7045–7059. doi: 10.1002/mma.8955 [31] P. A. Naik, Z. Eskandari and H. E. Shahraki, Flip and generalized flip bifurcations of a two-dimensional discrete-time chemical model, Mathematical Modelling and Numerical Simulation with Applications, 2021, 1(2), 95–101. doi: 10.53391/mmnsa.2021.01.009 [32] P. A. Naik, Z. Eskandari, H. E. Shahraki and K. M. Owolabi, Bifurcation analysis of a discrete-time prey-predator model, Bulletin of Biomathematics, 2023, 1(2), 111–123. [33] P. A. Naik, Z. Eskandari, M. Yavuz and J. Zu, Complex dynamics of a discrete-time Bazykin-Berezovskaya prey-predator model with a strong Allee effect, Journal of Computational and Applied Mathematics, 2022, 413, 114401. doi: 10.1016/j.cam.2022.114401 [34] P. A. Naik and K. R. Pardasani, Three dimensional finite element model to study calcium distribution in oocytes, Network Modeling Analysis in Health Informatics and Bioinformatics, 2017, 6, 16. doi: 10.1007/s13721-017-0158-5 [35] S. Noeiaghdam, M. Suleman and H. Budak, Solving a modified nonlinear epidemiological model of computer viruses by homotopy analysis method, Mathematical Sciences, 2018, 12, 211–222. doi: 10.1007/s40096-018-0261-5 [36] K. M. Owolabi, B. Karaagac and D. Baleanu, Pattern formation in superdiffusion predator-prey-like problems with integer- and noninteger-order derivatives, Mathematical Methods in the Applied Sciences, 2021, 44(5), 4018–4036. doi: 10.1002/mma.7007 [37] K. M. Owolabi, E. Pindza and A. Atangana, Analysis and pattern formation scenarios in the superdiffusive system of predation described with Caputo operator, Chaos Solitons & Fractals, 2021, 152(399), 111468. [38] A. K. G. Ozlem and M. Feckan, Stability, neimark-sacker bifurcation and chaos control for a prey-predator system with harvesting effect on predator, Miskolc Mathematical Notes, 2021, 22(2), 663–679. doi: 10.18514/MMN.2021.3450 [39] N. Sene, Analysis of a fractional-order chaotic system in the context of the Caputo fractional derivative via bifurcation and Lyapunov exponents, Journal of King Saud University-Science, 2021, 33(1), 101275. doi: 10.1016/j.jksus.2020.101275 [40] N. Sene, On the modeling and numerical discretizations of a chaotic system via fractional operators with and without singular kernels, Mathematical Sciences, 2023, 17, 517–537. doi: 10.1007/s40096-022-00478-w [41] N. Sene, Second-grade fluid with Newtonian heating under Caputo fractional derivative: analytical investigations via Laplace transforms, Mathematical Modeling and Numerical Simulation with Applications, 2022, 2(1), 13–25. doi: 10.53391/mmnsa.2022.01.002 [42] V. Volterra, Fluctuations in the abundance of a species considered mathematically, Nature, 1926, 118, 558–560. doi: 10.1038/118558a0 [43] W. X. Wang, Y. B. Zhang and C. Z. Liu, Analysis of a discrete-time predator-prey system with Allee effect, Ecological Complexity, 2011, 8(1), 81–85. doi: 10.1016/j.ecocom.2010.04.005 [44] M. Yavuz and N. Sene, Stability analysis and numerical computation of the fractional predator-prey model with the harvesting rate, Fractal and Fractional, 2020, 4, 35. doi: 10.3390/fractalfract4030035 [45] L. G. Yuan and Q. G. Yang, Bifurcation, invariant curve and hybrid control in a discrete-time predator-prey system, Applied Mathematical Modelling, 2015, 39(8), 2345–2362. doi: 10.1016/j.apm.2014.10.040 [46] M. Zhao, C. Li and J. Wang, Complex dynamic behaviors of a discrete-time predator-prey system, Journal of Applied Analysis and Computation, 2017, 7(2), 478–500. doi: 10.11948/2017030 -
-
-
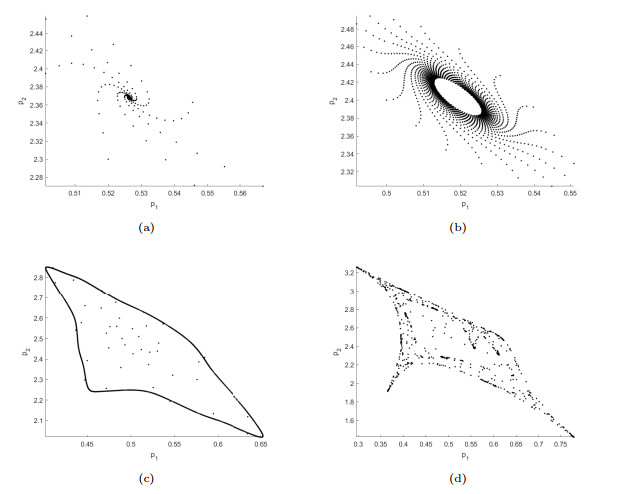
Figure 1.
Phase portraits of model (1.2). (a) A stable fixed point for
$ b=2.28 $ $ b=2.3111111 $ $ b=2.4 $ $ b=2.5 $ -
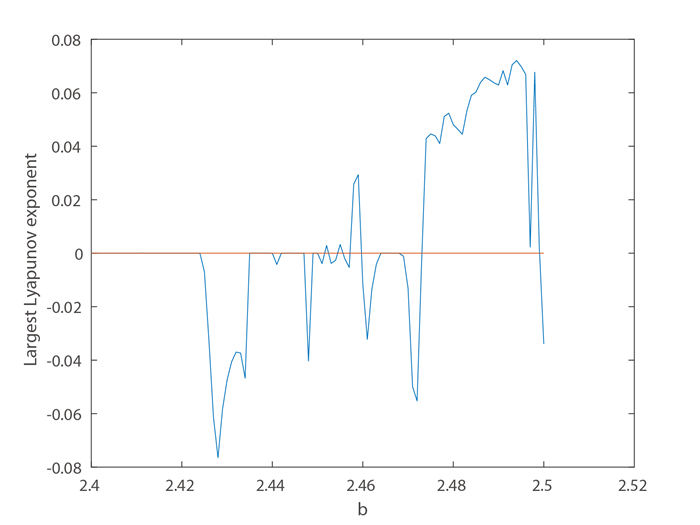
Figure 2.
The maximum Lyapunov exponent corresponding to Fig. 1.
-
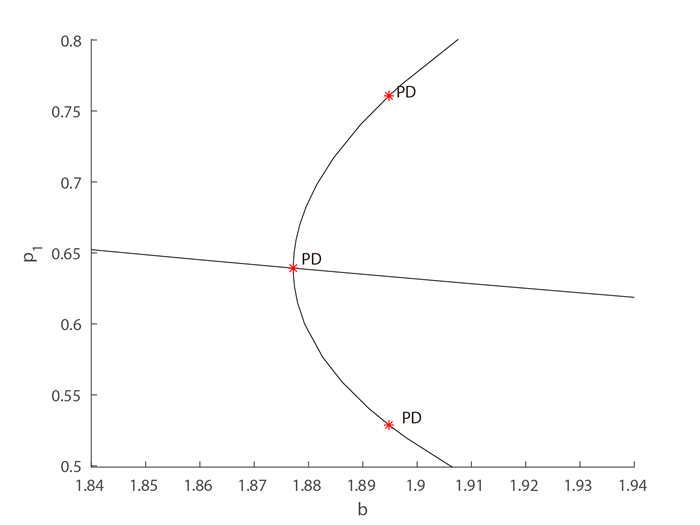
Figure 3.
The period-doubling cascad.
-
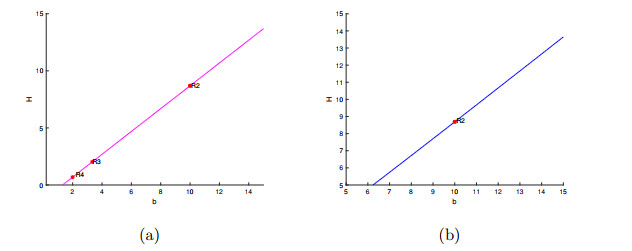
Figure 4.
(a), (b) The NS and PD curves, respectively
-
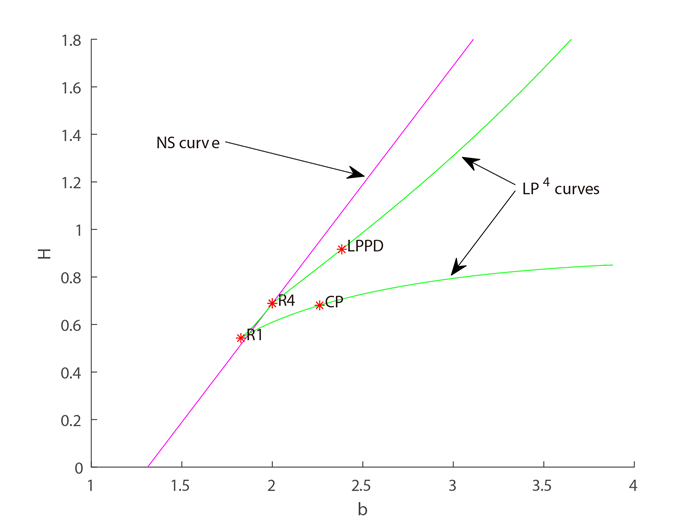
Figure 5.
Two-fold curves of the fourth iterate emanate from the R4 point of model (1.2).




 DownLoad:
DownLoad: