| Citation: |
Jianan Zhou, Lijuan Sheng. NUMBER OF LIMIT CYCLES OF A CASE OF POLYNOMIAL SYSTEM VIA THE STABILITY-CHANGING METHOD[J]. Journal of Applied Analysis & Computation, 2024, 14(1): 392-407. doi: 10.11948/20230249
|
NUMBER OF LIMIT CYCLES OF A CASE OF POLYNOMIAL SYSTEM VIA THE STABILITY-CHANGING METHOD
-
Abstract
In this paper, we study bifurcation of limit cycles bifurcating from a planar polynomial system with degree nine. More limit cycles can be obtained by using the stability-changing method compared to the Melnikov function method. We obtain 24 limit cycles bifurcating from a symmetrical compound loop with five saddles.
-
Keywords:
- Limit cycle /
- alien limit cycle /
- homoclinic loop /
- heteroclinic loop
-
-
References
[1] V. I. Arnol'd, Loss of stability of self-oscillations close to resonance and versal deformations of equivariant vector fields, Funktsional'nyi Analiz i ego Prilozheniya, 1977, 11(2), 1–10 [2] M. Caubergh, F. Dumortier and R. Roussarie, Alien limit cycles near a Hamiltonian 2-saddle cycle, C. R. Acad. Sci. Paris, Ser. I, 2005, 340(8), 587–592 doi: 10.1016/j.crma.2005.03.009 [3] X. Chen and M. Han, A linear estimate of the number of limit cycles for a piecewise smooth near-Hamiltonian system, Qualitative theory of dynamical systems, 2020, 19(2), 61 doi: 10.1007/s12346-020-00398-x [4] B. Coll, F. Dumortier and R. Prohens, Alien limit cycles in Lienard equations, Journal of Differential Equations, 2013, 254(3), 1582–1600 doi: 10.1016/j.jde.2012.11.005 [5] F. Dumortier and R. Roussarie, Abelian integrals and limit cycles, Journal of Differential Equations, 2006, 227(1), 116–165 doi: 10.1016/j.jde.2005.08.015 [6] W. Geng and Y. Tian, Bifurcation of limit cycles near heteroclinic loops in near-Hamiltonian systems, Communications in Nonlinear Science and Numerical Simulation, 2021, 95, 105666 doi: 10.1016/j.cnsns.2020.105666 [7] S. Gong and M. Han, Limit cycle bifurcations in a planar piecewise quadratic system with multiple parameters, Advances in Difference Equations, 2020, 2020(1), 1–16 doi: 10.1186/s13662-019-2438-0 [8] M. Han, Cyclicity of planar homoclinic loops and quadratic integrable systems, Science in China Series A: Mathematics, 1997, 40(12), 1247–1258 doi: 10.1007/BF02876370 [9] M. Han, Asymptotic expansions of melnikov functions and limit cycle bifurcations, International Journal of Bifurcation and Chaos, 2012, 22(12), 1250296 doi: 10.1142/S0218127412502963 [10] M. Han and J. Chen, The number of limit cycles bifurcating from a pair of homoclinic loops, Science in China Series A Mathematics, 2000, 30, 401–414 [11] M. Han, S. Hu and X. Liu, On the stability of double homoclinic and heteroclinic cycles, Nonlinear Analysis: Theory, Methods & Applications, 2003, 53(5), 701–713 [12] M. Han and W. Lu, Hopf bifurcation of limit cycles by perturbing piecewise integrable systems, Bulletin des Sciences Mathématiques, 2020, 161, 102866 doi: 10.1016/j.bulsci.2020.102866 [13] M. Han, V. G. Romanovski and X. Zhang, Equivalence of the Melnikov function method and the averaging method, Qualitative Theory of Dynamical Systems, 2016, 15(2), 471–479 doi: 10.1007/s12346-015-0179-3 [14] M. Han and J. Yang, The maximum number of zeros of functions with parameters and application to differential equations, J. Nonlinear Model. Anal, 2021, 3, 13–34 [15] M. Han and Z. Zhang, Cyclicity 1 and 2 conditions for a 2-polycycle of integrable systems on the plane, Journal of Differential Equations, 1999, 155(2), 245–261 doi: 10.1006/jdeq.1998.3585 [16] M. Han and H. Zhu, The loop quantities and bifurcations of homoclinic loops, Journal of Differential Equations, 2007, 234(2), 339–359 doi: 10.1016/j.jde.2006.11.009 [17] W. Hou and S. Liu, Melnikov functions for a class of piecewise Hamiltonian systems, Journal of Nonlinear Modeling & Analysis, 2023, 5(1), 123–145 [18] P. Joyal and C. Rousseau, Saddle quantities and applications, Journal of Differential Equations, 1989, 78(2), 374–399 doi: 10.1016/0022-0396(89)90069-7 [19] F. Liang and M. Han, Limit cycles near generalized homoclinic and double homoclinic loops in piecewise smooth systems, Chaos, Solitons & Fractals, 2012, 45(4), 454–464 [20] F. Liang, M. Han and V. G. Romanovski, Bifurcation of limit cycles by perturbing a piecewise linear hamiltonian system with a homoclinic loop, Nonlinear Analysis: Theory, Methods & Applications, 2012, 75(11), 4355–4374 [21] F. Liang, M. Han and X. Zhang, Bifurcation of limit cycles from generalized homoclinic loops in planar piecewise smooth systems, Journal of Differential Equations, 2013, 255(12), 4403–4436 doi: 10.1016/j.jde.2013.08.013 [22] L. Sheng and M. Han, Bifurcation of limit cycles from a compound loop with five saddles, J. Appl. Anal. Comput, 2019, 9(6), 2482–2495 [23] L. Sheng, M. Han and Y. Tian, On the number of limit cycles bifurcating from a compound polycycle, International Journal of Bifurcation and Chaos, 2020, 30(07), 2050099 doi: 10.1142/S0218127420500996 [24] Y. Tian and M. Han, Hopf and homoclinic bifurcations for near-Hamiltonian systems, Journal of Differential Equations, 2017, 262(4), 3214–3234 doi: 10.1016/j.jde.2016.11.026 [25] S. Wang, P. Yu and J. Li, Bifurcation of limit cycles in $Z_10$-equivariant vector fields of degree 9, International Journal of Bifurcation and Chaos, 2006, 16(08), 2309–2324 doi: 10.1142/S0218127406016070 [26] Y. Xiong and M. Han, Limit cycle bifurcations near homoclinic and heteroclinic loops via stability-changing of a homoclinic loop, Chaos Solitons & Fractals, 2015, 78, 107–117 [27] Y. Xiong and M. Han, Limit cycle bifurcations in discontinuous planar systems with multiple lines, J. Appl. Anal. Comput, 2020, 10(1), 361–377 [28] Y. Xiong and M. Han, Limit cycles appearing from a generalized heteroclinic loop with a cusp and a nilpotent saddle, Journal of Differential Equations, 2021, 303, 575–607 doi: 10.1016/j.jde.2021.09.031 [29] J. Yang, Y. Xiong and M. Han, Limit cycle bifurcations near a 2-polycycle or double 2-polycycle of planar systems, Nonlinear Analysis: Theory, Methods & Applications, 2014, 95, 756–773 [30] J. Yang, P. Yu and M. Han, Limit cycle bifurcations near a double homoclinic loop with a nilpotent saddle of order m, Journal of Differential Equations, 2019, 266(1), 455–492 doi: 10.1016/j.jde.2018.07.042 [31] J. Yang and L. Zhao, Bounding the number of limit cycles of discontinuous differential systems by using Picard-Fuchs equations, Journal of Differential Equations, 2018, 264(9), 5734–5757 doi: 10.1016/j.jde.2018.01.017 [32] P. Yu, M. Han and J. Li, An improvement on the number of limit cycles bifurcating from a nondegenerate center of homogeneous polynomial systems, International Journal of Bifurcation and Chaos, 2018, 28(06), 1850078 doi: 10.1142/S0218127418500785 [33] P. Yu, M. Han and X. Zhang, Eighteen limit cycles around two symmetric foci in a cubic planar switching polynomial system, Journal of Differential Equations, 2021, 275, 939–959 doi: 10.1016/j.jde.2020.11.001 [34] P. Yu and Y. Tian, Twelve limit cycles around a singular point in a planar cubic-degree polynomial system, Communications in Nonlinear Science and Numerical Simulation, 2014, 19(8), 2690–2705 doi: 10.1016/j.cnsns.2013.12.014 -
-
Figures(6) / Tables(1)
Export File
Citation
Jianan Zhou, Lijuan Sheng. NUMBER OF LIMIT CYCLES OF A CASE OF POLYNOMIAL SYSTEM VIA THE STABILITY-CHANGING METHOD[J]. Journal of Applied Analysis & Computation, 2024, 14(1): 392-407. doi: 10.11948/20230249
Format
Content
DownLoad:
-
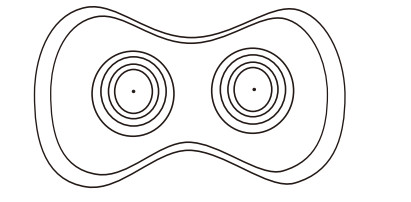
Figure 1.
The image of
$ L_{0} $ -
Figure 2.
The distribution of 10 limit cycles
-
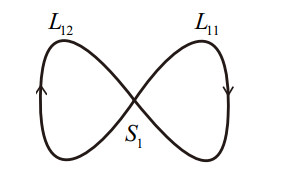
Figure 3.
The image of
$ L_{1} $ -
Figure 4.
The distribution of 7 limit cycles
-
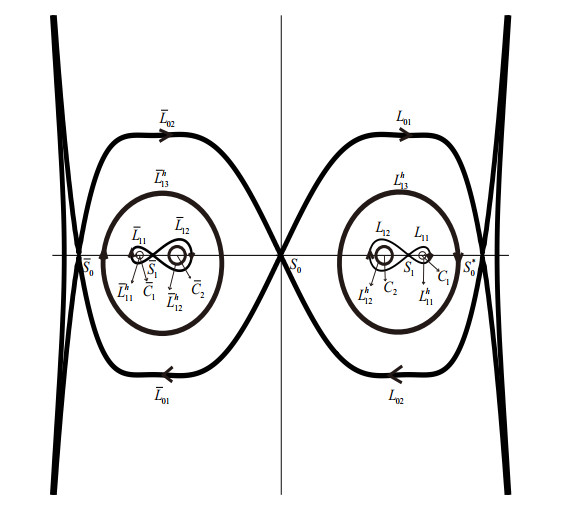
Figure 5.
The image of
$ L_0 $ $ L_1 $ $ \bar L_1 $ -
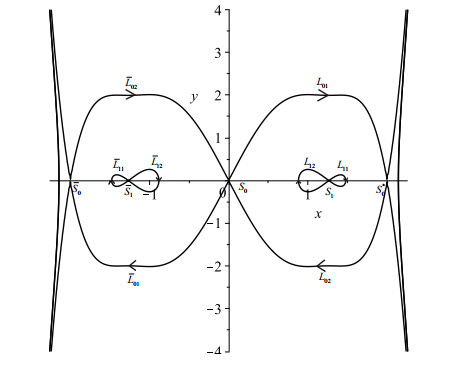
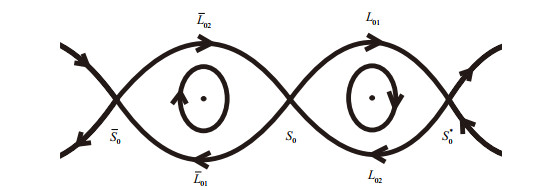
Figure 6.
The phase portrait of system (1.3)