| Citation: |
Yanchao He, Yuzhen Bai. EXPONENTIAL STABILITY AND APPLICATIONS OF SWITCHED POSITIVE LINEAR IMPULSIVE SYSTEMS WITH TIME-VARYING DELAYS AND ALL UNSTABLE SUBSYSTEMS[J]. Journal of Applied Analysis & Computation, 2024, 14(4): 2369-2391. doi: 10.11948/20230392
|
EXPONENTIAL STABILITY AND APPLICATIONS OF SWITCHED POSITIVE LINEAR IMPULSIVE SYSTEMS WITH TIME-VARYING DELAYS AND ALL UNSTABLE SUBSYSTEMS
-
Abstract
The global uniform exponential stability of switched positive linear impulsive systems with time-varying delays and all unstable subsystems is studied in this paper, which includes two types of distributed time-varying delays and discrete time-varying delays. Switching behaviors dominating the switched systems can be either stabilizing or destabilizing in the new designed switching sequence. We design new linear programming algorithm process to find the feasible ratio of stabilizing switching behaviors, which can be compensated by unstable subsystems, destabilizing switching behaviors, and impulses. Specifically, we add a kind of nonnegative impulses which is consistent with the switching behaviors for the systems. Employing a multiple co-positive Lyapunov–Krasovskii functional, we present several new sufficient stability criteria and design new switching sequence. Then, we apply the obtained stability criteria to the exponential consensus of linear delayed multi-agent systems, and obtain the new exponential consensus criteria. Three simulations are provided to demonstrate the proposed stability criteria.
-
Keywords:
- Exponential stability /
- switched systems /
- impulses /
- distributed time-varying delays
-
-
References
[1] A. Y. Aleksandrov and O. Mason, On diagonal stability of positive systems with switches and delays, Autom. Remote Control, 2018, 79(12), 2114–2127. doi: 10.1134/S0005117918120020 [2] G. Chen and Y. Yang, Finite-time stability of switched positive linear systems, Int. J. Robust Nonlinear Control, 2014, 24(1), 179–190. doi: 10.1002/rnc.2870 [3] Q. Chen, Z. Liu, Y. Tan and J. Yang, Analysis of a stochastic nonautonomous hybrid population model with impulsive perturbations, J. Appl. Anal. Comput., 2023, 13(5), 2365–2386. [4] M. Hu, Y. Wang, J. Xiao and W. Yang, $L_{1}$-gain analysis and control of impulsive positive systems with interval uncertainty and time delay, J. Frankl. Inst., 2019, 356(16), 9180–9205. doi: 10.1016/j.jfranklin.2019.08.010 CrossRef $L_{1}$-gain analysis and control of impulsive positive systems with interval uncertainty and time delay" target="_blank">Google Scholar
[5] Y. Ju, F. Meng and Y. Sun, Exponential stability of switched linear impulsive time-varying system and its application, J. Frankl. Inst., 2022, 359(11), 5619–5633. doi: 10.1016/j.jfranklin.2022.05.024 [6] S. Khoa and V. Le, Exponential stability analysis for a class of switched nonlinear time-varying functional differential systems, Nonlinear Anal. Hybrid Syst., 2022, 44, 101177. doi: 10.1016/j.nahs.2022.101177 [7] S. Kim, S. A. Campbell and X. Liu, Delay independent stability of linear switching systems with time delay, J. Math. Anal. Appl., 2008, 339(2), 785–801. doi: 10.1016/j.jmaa.2007.06.075 [8] S. Li and Z. Xiang, Stability and $L_{1}$-gain analysis for positive switched systems with time-varying delay under state-dependent switching, Circuits Syst. Signal Process., 2016, 35(3), 1045–1062. doi: 10.1007/s00034-015-0099-0 CrossRef $L_{1}$-gain analysis for positive switched systems with time-varying delay under state-dependent switching" target="_blank">Google Scholar
[9] S. Li and Z. Xiang, Stability and $L_{1}$-gain control for positive impulsive switched systems with mixed time-varying delays, IMA J. Math. Control I., 2016, 34(4), 1339–1358. [10] S. Li, Z. Xiang and H. R. Karimi, Stability and $L_{1}$-gain controller design for positive switched systems with mixed time-varying delays, Appl. Math. Comput., 2013, 222, 507–518. [11] J. Lian, C. Li and B. Xia, Sampled-data control of switched linear systems with application to an F-18 aircraft, IEEE Trans. Ind. Electron., 2016, 64(2), 1332–1340. [12] D. Liberzon, Switching in Systems and Control, Birkhäuser, Boston, Mass, USA, 2003. [13] L. Liu, X. Zhao and D. Wu, Stability of switched positive linear time-delay systems, IET Control Theory & Appl., 2019, 13(7), 912–919. [14] T. Liu, B. Wu, L. Liu and Y. Wang, Asynchronously finite-time control of discrete impulsive switched positive time-delay systems, J. Frankl. Inst., 2015, 352(10), 4503–4514. doi: 10.1016/j.jfranklin.2015.06.015 [15] Z. Liu, Y. Wang and G. Zhao, Exponential stability for positive switched linear systems with delays and impulses, in: Proceedings of the 33rd Chinese Control Conference, IEEE, 2014, 2469–2474. [16] Z. Liu, X. Zhang, X. Lu and T. Hou, Exponential stability of impulsive positive switched systems with discrete and distributed time-varying delays, Int. J. Robust Nonlin. Control, 2019, 29(10), 3125–3138. doi: 10.1002/rnc.4543 [17] Z. Liu, X. Zhang, X. Lu and Q. Liu, Stabilization of positive switched delay systems with all modes unstable, Nonlinear Anal. Hybrid Syst., 2018, 29, 110–120. doi: 10.1016/j.nahs.2018.01.004 [18] Z. She and B. Xue, Discovering multiple Lyapunov functions for switched hybrid systems, SIAM J. Control Optim., 2014, 52(5), 3312–3340. doi: 10.1137/130934313 [19] L. Shu, X. Shu, Q. Zhu and F. Xu, Existence and exponential stability of mild solutions for second-order neutral stochastic functional differential equation with random impulses, J. Appl. Anal. Comput., 2021, 11(1), 59–80. [20] S. Solmaz, R. Shorten, K. Wulff and F. Cairbre, A design methodology for switched discrete time linear systems with applications to automotive roll dynamics control, Automatica, 2008, 44(9), 2358–2363. doi: 10.1016/j.automatica.2008.01.014 [21] S. Sun, X. Li and R. Zhong, An open-closed-loop iterative learning control approach for nonlinear switched systems with application to freeway traffic control, In. J. Syst. Sci., 2017, 48(13), 2752–2763. doi: 10.1080/00207721.2017.1346153 [22] Y. Sun, Y. Tian and X. Xie, Stabilization of positive switched linear systems and its application in consensus of multiagent systems, IEEE Trans. Autom. Control, 2017, 62(12), 6608–6613. doi: 10.1109/TAC.2017.2713951 [23] Z. Sun and S. S. Ge, Stability Theory of Switched Dynamical Systems, Springer, London, 2011. [24] M. Xiang and Z. Xiang, Finite-time $L_{1}$ control for positive switched linear systems with time-varying delay, Commun. Nonl. Sci. Numer. Simul., 2013, 18(11), 3158–3166. doi: 10.1016/j.cnsns.2013.04.014 CrossRef $L_{1}$ control for positive switched linear systems with time-varying delay" target="_blank">Google Scholar
[25] N. Xu, Y. Chen, A. Xue and G. Zong, Finite-time stabilization of continuous-time switched positive delayed systems, J. Frankl. Inst., 2022, 359(1), 255–271. doi: 10.1016/j.jfranklin.2021.04.022 [26] J. You and S. Sun, Mixed boundary value problems for a class of fractional differential equations with impulses, J. Nonl. Mod. Anal., 2021, 3(2), 263–273. [27] Y. Zhang, W. Huang and X. Yang, A switching law to stabilize an unstable switched linear system, J. Nonl. Mod. Anal., 2021, 3(3), 349–364. [28] X. Zhao, Y. Yin, L. Liu and X. Sun, Stability analysis and delay control for switched positive linear systems, IEEE Trans. Autom. Control, 2017, 63(7), 2184–2190. [29] Z. Zhou, Y. Wang, W. Yang and M. Hu, Exponential stability of switched positive systems with all modes being unstable, Int. J. Robust Nonlin. Control, 2020, 30(12), 4600–4610. doi: 10.1002/rnc.5005 [30] Z. Zhou, Y. Wang, W. Yang and M. Hu, Exponential stability of switched positive systems with unstable modes and distributed delays, J. Frankl. Inst., 2022, 359(1), 66–83. doi: 10.1016/j.jfranklin.2021.01.033 -
-
Figures(8)
Export File
Citation
Yanchao He, Yuzhen Bai. EXPONENTIAL STABILITY AND APPLICATIONS OF SWITCHED POSITIVE LINEAR IMPULSIVE SYSTEMS WITH TIME-VARYING DELAYS AND ALL UNSTABLE SUBSYSTEMS[J]. Journal of Applied Analysis & Computation, 2024, 14(4): 2369-2391. doi: 10.11948/20230392
Format
Content
DownLoad:
-
Figure 1.
The sketch map process of adjusting the original switching sequence with
$ m=4 $ $ [t_{l1}, t_{l2}] $ $ [t_{l1}, t_{{l1}+1}] $ $ [t_{{l1}+1}, t_{l2}] $ $ |M_{k}^{\uparrow}|= m_{1} $ $ |M_{k}^{\downarrow}|= m_{2} $ $ m_{1}+m_{2}=4 $ $ m_{1}=1 $ $ m_{2}=3 $ -
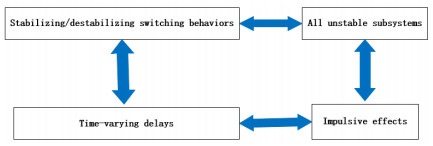
Figure 2.
The influence factors of GUES for SPLISs (1.1) and (1.2).
-
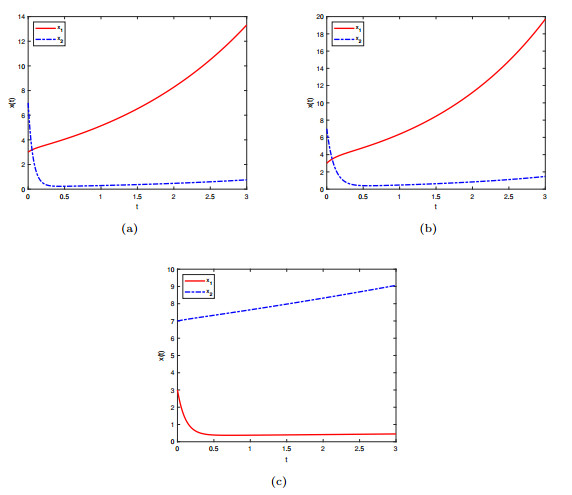
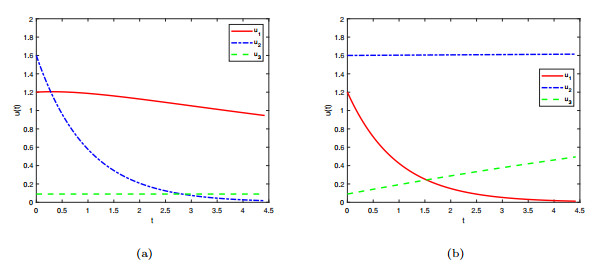
Figure 3.
The state trajectories of three subsystems of SPLISs (1.1).
-
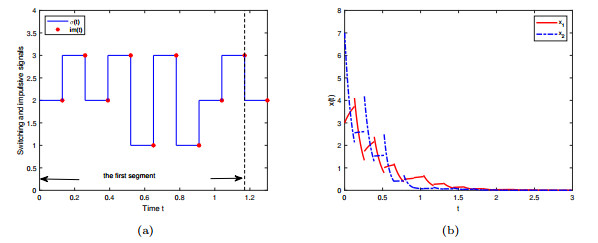
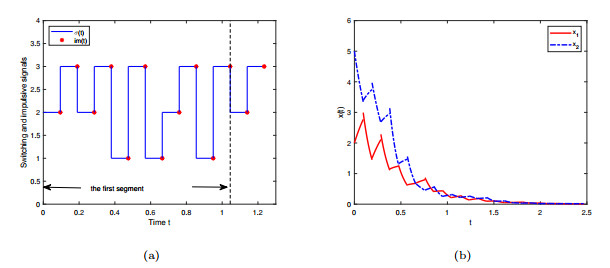
Figure 4.
The signals and state trajectories of SPLISs (1.1).
-
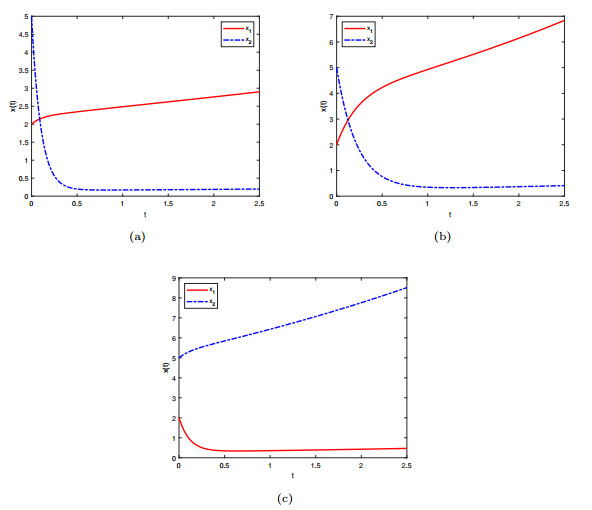
Figure 5.
The state trajectories of three subsystems of SPLISs (1.2).
-
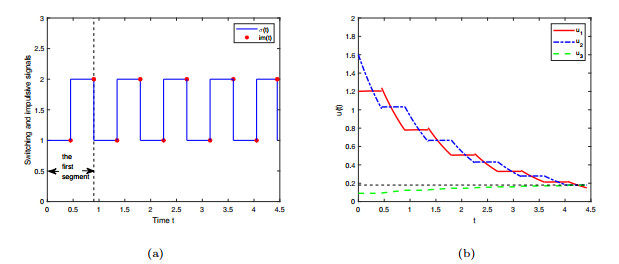
Figure 6.
The signals and state trajectories of SPLISs (1.2).
-
Figure 7.
The state trajectories of two subsystems of systems (4.1).
-
Figure 8.
The signals and state trajectories of systems (4.1).