| Citation: | Lili Jia, Juan Huang, Changyou Wang. GLOBAL STABILITY OF PERIODIC SOLUTION FOR A 3-SPECIES NONAUTONOMOUS RATIO-DEPENDENT DIFFUSIVE PREDATOR-PREY SYSTEM[J]. Journal of Applied Analysis & Computation, 2024, 14(4): 2392-2410. doi: 10.11948/20230397 |
GLOBAL STABILITY OF PERIODIC SOLUTION FOR A 3-SPECIES NONAUTONOMOUS RATIO-DEPENDENT DIFFUSIVE PREDATOR-PREY SYSTEM
-
Abstract
A 3-species nonautonomous ratio-dependent diffusive predator-prey system is considered in this article. Firstly, by utilizing a comparison principle and fixed point theorem, the existence of solution which is space homogenous strictly positive and periodic for the above system is obtained. And the obtained conditions ensuring the existence of solution can be very easily verified. At the same time, we develop some new analysis techniques as a byproduct. Furthermore, with the help of the upper and lower solutions (UALS) approach for the parabolic partial differential equations and Lyapunov theory, we aim at the globally asymptotically stability problems of the solutions, and some judgment criteria are achieved. Finally, we give some numerical simulations results which validate the theoretical findings of this article.
-
Keywords:
- Nonautonomous /
- reaction-diffusion /
- predator-prey /
- global stability /
- ratio-dependent
-

-
References
[1] T. Agrawal and M. Saleem, Complex dynamics in a ratio-dependent two-predator one-prey model, Computational & Applied Mathematics, 2015, 34(1), 265–274. [2] R. Arditi and L. R. Ginzburg, Coupling in predator-prey dynamics: Ratio-dependence, Journal of Theoretical Biology, 1989, 139(3), 311–326. doi: 10.1016/S0022-5193(89)80211-5 [3] W. Basener, Topology and its Applications, Hoboken, NJ: John Wiley & Sons, 2006. [4] M. Belabbas, A. Ouahab and F. Souna, Rich dynamics in a stochastic predator-prey model with protection zone for the prey and multiplicative noise applied on both species, Nonlinear Dynamics, 2021, 106(3), 2761–2780. doi: 10.1007/s11071-021-06903-4 [5] C. Conser, D. L. Angelis, J. S. Ault and D. B. Olson, Effects of spatial grouping on the functional response of predators, Theoretical Population Biology, 1999, 56(1), 65–75. doi: 10.1006/tpbi.1999.1414 [6] E. Cruz, M. Negreanu and J. I. Tello, Asymptotic behavior and global existence of solutions to a two-species chemotaxis system with two chemicals, Zeitschrift für angewandte Mathematik und Physik, 2018, 64(4), ID: 107. [7] S. M. Fu and S. B. Cui, Persistence in a periodic competitor-competitor-mutualist diffusion system, Journal of Mathematical Analysis and Applications, 2001, 263, 234–245. doi: 10.1006/jmaa.2001.7612 [8] Y. J. Gao and B. T. Li, Dynamics of a ratio-dependent predator-prey system with a strong Allee effect, Discrete and Continuous Dynamical Systems-Series B, 2013, 18(9), 2283–2313. doi: 10.3934/dcdsb.2013.18.2283 [9] K. Guo and W. B. Ma, Existence of positive periodic solutions for a periodic predator-prey model with fear effect and general functional responses, Advances in Continuous and Discrete Models, 2023, 2023, Article ID: 22. [10] M. Haque, Ratio-dependent predator-prey models of interacting populations, Bulletin of Mathematical Biology, 2009, 71(2), 430–452. doi: 10.1007/s11538-008-9368-4 [11] X. Jiang, G. Meng and Z. K. She, Existence of periodic solutions in a nonautonomous food web with Beddington-DeAngelis functional response, Applied Mathematics Letters, 2017, 71, 59–66. doi: 10.1016/j.aml.2017.03.018 [12] X. Jiang, R. Zhang and Z. K. She, Dynamics of a diffusive predator-prey system with ratio- dependent functional response and time delay, International Journal of Biomathematics, 2020, 13(6), Article ID: 2050036. [13] C. Jost, O. Arino and R. Arditi, About deterministic extinction in ratio-dependent predator-prey models, Bulletin of Mathematical Biology, 1999, 61(1), 19–32. doi: 10.1006/bulm.1998.0072 [14] D. Kesh, A. K. Sarkar and A. B. Roy, Persistence of two prey-one predator system with ratio- dependent predator influence, Mathematical Methods in the Applied Sciences, 2000, 23(4), 347–356. doi: 10.1002/(SICI)1099-1476(20000310)23:4<347::AID-MMA117>3.0.CO;2-F [15] H. H. Khalil, Nonlinear Systems, 3rd ed, Englewood Cliffs, NJ: Prentice Hall, 2002. [16] K. I. Kim and Z. Lin, Blowup in a three-species cooperating model, Applied Mathematics Letters, 2004, 17, 89–94. doi: 10.1016/S0893-9659(04)90017-1 [17] W. Ko and I. Ahn, A diffusive one-prey and two-competing-predator system with a ratio- dependent functional response: I, long time behavior and stability of equilibria, Journal of Mathematical Analysis and Applications, 2013, 397(1), 9–28. doi: 10.1016/j.jmaa.2012.07.026 [18] W. Ko and I. Ahn, A diffusive one-prey and two-competing-predator system with a ratio- dependent functional response: Ⅱ stationary pattern formation, Journal of Mathematical Analysis and Applications, 2013, 397(1), 29–45. doi: 10.1016/j.jmaa.2012.07.025 [19] A. Leung, A study of 3-species prey-predator reaction-diffusions by monotone schemes, Journal of Mathematical Analysis and Applications, 1984, 100, 583–604. doi: 10.1016/0022-247X(84)90103-3 [20] H. Y. Li, Z. K. She, Uniqueness of periodic solutions of a nonautonomous density-dependent predator-prey system, Journal of Mathematical Analysis and Applications, 2015, 422, 886–905. doi: 10.1016/j.jmaa.2014.09.008 [21] L. Li, Z. Jin and J. Li, Periodic solutions in a herbivore-plant system with time delay and spatial diffusion, Applied Mathematical Modelling, 2016, 40(7–8), 4765–4777. doi: 10.1016/j.apm.2015.12.003 [22] A. J. Lotka, Elements of Physical Biology, New York: Williams and Wilkins, 1925. [23] P. S. Mandal, Noise-induced extinction for a ratio-dependent predator-prey model with strong Allee effect in prey, Physica A: Statistical Mechanics and its Applications, 2018, 496, 40–52. doi: 10.1016/j.physa.2017.12.057 [24] P. Y. H. Pang and M. Wang, Strategy and stationary pattern in a three-species predator-prey model, Journal of Differential Equations, 2004, 200(2), 245–273. doi: 10.1016/j.jde.2004.01.004 [25] C. V. Pao, Global asymptotic stability of Lotka-Volterra 3-species reaction-diffusion systems with time delays, Journal of Mathematical Analysis and Applications, 2003, 281, 86–204. doi: 10.1016/S0022-247X(02)00525-5 [26] C. V. Pao and Y. M. Wang, Numerical solutions of a three-competition Lotka-Volterra system, Applied Mathematics and Computation, 2008, 204, 423–440. doi: 10.1016/j.amc.2008.06.057 [27] N. Sk, P. K. Tiwari and S. Pal, A delay nonautonomous model for the impacts of fear and refuge in a three species food chain model with hunting cooperation, Mathematics and Computers in Simulation, 2022, 192, 136–166. doi: 10.1016/j.matcom.2021.08.018 [28] X. Tian and S. J. Guo, Spatio-temporal patterns of predator-prey model with Allee effect and constant stocking rate for predator, International Journal of Bifurcation and Chaos, 2021, 31(16), Article ID: 2150249. [29] J. P. Tripathi, S. Bugalia, V. Tiwari and Y. Kang, A predator-prey model with Crowley-Martin functional response: A nonautonomous study, Natural Resource Modelling, 2020, 33, e12287. doi: 10.1111/nrm.12287 [30] C. Vargas-De-Leon, Global stability of nonhomogeneous coexisting equilibrium state for the multispecies Lotka-Volterra mutualism models with diffusion, Mathematical Methods in the Applied Sciences, 2022, 45(4), 2123–2130. doi: 10.1002/mma.7912 [31] V. Volterra, Variazionie fluttuazioni del numero d'individui in specie animali conviventi, Memorie deU'Accademia del Lincei, 1926, 2, 31–113. [32] C. Y. Wang, Existence and stability of periodic solutions for parabolic systems with time delays, Journal of Mathematical Analysis and Application, 2008, 339(2), 1354–1361. doi: 10.1016/j.jmaa.2007.07.082 [33] C. Y. Wang, L. R. Li, Y. Q. Zhou and R. Li, On a delay ratio-dependent predator-prey system with feedback controls and shelter for the prey, International Journal of Biomathematics, 2018, 11(7), Article ID: 1850095. [34] C. Y. Wang, N. Li, Y. Q. Zhou, X. C. Pu and R. Li, On a multi-delay Lotka-Volterra predator-prey model with feedback controls and prey diffusion, Acta Mathematica Scientia, Series B, 2019, 39(2), 429–448. doi: 10.1007/s10473-019-0209-3 [35] C. Y. Wang, S. Wang and L. R. Li, Periodic solution and almost periodic solution of a nonmonotone reaction-diffusion system with time delay, Acta Mathematica Scientia, 2010, 30A, 517–524. (in Chinese). [36] C. Y. Wang, S. Wang, F. P. Yang and L. R. Li, Global asymptotic stability of positive equilibrium of three-species Lotka-Volterra mutualism models with diffusion and delay effects, Applied Mathematical Modelling, 2010, 34(12), 4278–4288. doi: 10.1016/j.apm.2010.05.003 [37] C. Y. Wang, Y. Q. Zhou, Y. H. Li and R. Li, Well-posedness of a ratio-dependent Lotka-Volterra system with feedback control, Boundary Value Problems, 2018, 2018, Article ID: 117. [38] J. F. Wang, Spatiotemporal patterns of a homogeneous diffusive predator-prey system with Holling type Ⅲ functional response, Journal of Dynamics and Differential Equations, 2017, 29, 1383–1409. doi: 10.1007/s10884-016-9517-7 [39] M. X. Wang and Q. Y. Zhang, Dynamics for the diffusive Leslie-Gower model with double free boundaries, Discrete and Continuous Dynamical Systems -A, 2018, 38(5), 2591–2591. doi: 10.3934/dcds.2018109 [40] F. R. Wei, C. H. Wang and S. L. Yuan, Spatial dynamics of a diffusive predator-prey model with Leslie-Gower functional response and strong Allee effect, Journal of Nonlinear Modeling and Analysis, 2020, 2(2), 267–285. [41] D. Y. Wu and H. Y. Zhao, Spatiotemporal dynamics of a diffusive predator-prey system with Allee effect and threshold hunting, Journal of Nonlinear Science, 2020, 30, 1015–1054. doi: 10.1007/s00332-019-09600-0 [42] Y. M. Wu, F. D. Chen and C. F. Du, Dynamic behaviors of a nonautonomous predator-prey system with Holling type Ⅱ schemes and a prey refuge, Advances in Difference Equations, 2021, 2021, Article ID: 62. [43] X. P. Yan and C. H. Zhang, Spatiotemporal dynamics in a diffusive predator-prey system with Beddington-DeAngelis functional response, Qualitative Theory of Dynamical Systems, 2022, 21(4), Article ID: 166. [44] W. B. Yang, Y. L. Li, J. H. Wu and H. X. Li, Dynamics of a food chain model with ratio-dependent and modified Leslie-Gower functional responses, Discrete and Continuous Dynamical Systems-B, 2015, 20(7), 2269–2290. doi: 10.3934/dcdsb.2015.20.2269 [45] T. Yu, Q. L. Wang and S. Q. Zhai, Exploration on dynamics in a ratio-dependent predator-prey bioeconomic model with time delay and additional food supply, Mathematical Biosciences and Engineering, 2023, 20(8), 15094–15119. doi: 10.3934/mbe.2023676 [46] G. Zhang, W. Wang and X. Wang, Coexistence states for a diffusive one-prey and two-predators model with B-D functional response, Journal of Mathematical Analysis and Applications, 2012, 387(2), 931–948. doi: 10.1016/j.jmaa.2011.09.049 [47] L. Zhang and X. X. Bao, Propagation dynamics of a three-species nonlocal competitive- cooperative system, Nonlinear Analysis: Real World Applications, 2021, 58, ID: 103230. [48] X. Zhao and R. Z. Yang, Dynamical property analysis of a delayed diffusive predator-prey model with fear effect, Journal of Nonlinear Modeling and Analysis, 2023, 5(1), 1–23. [49] S. Zheng, A reaction-diffusion system of a competitor-competitor-mutualist model, Journal of Mathematical Analysis and Applications, 1993, 124, 254–280. [50] J. Zhou and C. G. Kim, Positive solutions for a Lotka-Volterra prey-predator model with cross- diffusion and Holling type-Ⅱ functional response, Science China-Mathematics, 2014, 57(5), 991–1010. doi: 10.1007/s11425-013-4711-0 -
-
-
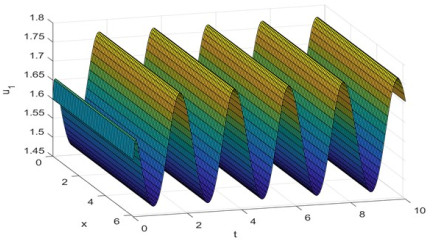
Figure 5.1.
Evolution process of the density for the species
$ {u_1}(x,t) $ -
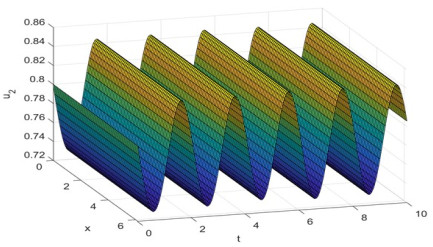
Figure 5.2.
Evolution process of the density for the species
$ {u_2}(x,t) $ -
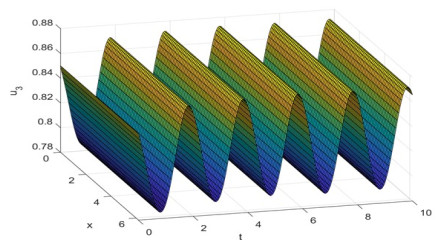
Figure 5.3.
Evolution process of the density for the species
$ {u_3}(x,t) $




 DownLoad:
DownLoad: