| Citation: | Zhouhong Li, Xiaofang Meng, Kaipeng Hu, Yu Fei. QUASI-PROJECTIVE SYNCHRONIZATION ANALYSIS FOR DELAYED STOCHASTIC QUATERNION-VALUED NEURAL NETWORKS VIA STATE-FEEDBACK CONTROL STRATEGY[J]. Journal of Applied Analysis & Computation, 2024, 14(4): 2411-2430. doi: 10.11948/20230399 |
QUASI-PROJECTIVE SYNCHRONIZATION ANALYSIS FOR DELAYED STOCHASTIC QUATERNION-VALUED NEURAL NETWORKS VIA STATE-FEEDBACK CONTROL STRATEGY
-
Abstract
In this paper, we explore the complete synchronization and quasi-projective synchronization in a class of stochastic delayed quaternion-valued neural networks, utilizing a state-feedback control scheme. The studied neural networks into real-valued networks are short of known decomposing, by designing a very general nonlinear controller, according to the quaternion form It? formula with a number of inequality techniques in the configuration of quaternion domain, we obtained a quasi-projective synchronization criterion for drive-response networks. Moreover, we estimate the error margin for quasi-projective synchronization. At last, the theoretical results are confirmed by a numerical simulation.
-

-
References
[1] S. Blythe, X. Mao and X. Liao, Stability of stochastic delay neural networks, J. Franklin. I., 2001, 338(4), 481–495. doi: 10.1016/S0016-0032(01)00016-3 [2] S. Chen and J. Cao, Projective synchronization of neural networks with mixed time-varying delays and parameter mismatch, Nonlinear Dynam., 2012, 67(2), 1397–1406. doi: 10.1007/s11071-011-0076-5 [3] X. Chen, Z. Li, Q. Song, J. Hua and Y. Tan, Robust stability analysis of quaternion-valued neural networks with time delays and parameter uncertainties, Neural Networks, 2017, 91, 55–65. doi: 10.1016/j.neunet.2017.04.006 [4] L. Dai and Y. Hou, Mean-square exponential input-to-state stability of stochastic quaternion-valued neural networks with time-varying delays, Adv. Differ. Equ., 2021, 362, 1–15. [5] H. Deng and H. Bao, Fixed-time synchronization of quaternion-valued neural networks, Physica A, 2019, 527, 121351. doi: 10.1016/j.physa.2019.121351 [6] Q. Gan, R. Xu and X. Kang, Synchronization of chaotic neural networks with mixed time delays, Commun. Nonlinear. Sci., 2011, 16(2), 966–974. doi: 10.1016/j.cnsns.2010.04.036 [7] D. Ghosh and S. Banerjee, Projective synchronization of time-varying delayed neural network with adaptive scaling factors, Chaos Solition Fract., 2013, 53, 1–9. doi: 10.1016/j.chaos.2013.04.007 [8] R. Guo, W. Lv and Z. Zhang, Quasi-projective synchronization of stochastic complex-valued neural networks with time-varying delay and mismatched parameters, Neurocomputing, 2020, 415, 184–192. doi: 10.1016/j.neucom.2020.07.033 [9] J. Hu, S. Zhong and L. Liang, Exponential stability analysis of stochastic delayed cellular neural network, Chaos Solition Fract., 2006, 27(4), 1006–1010. doi: 10.1016/j.chaos.2005.04.067 [10] C. Huang and J. Cao, Almost sure exponential stability of stochastic cellular neural networks with unbounded distributed delays, Neurocomputing, 2009, 72(13–15), 3352–3356. doi: 10.1016/j.neucom.2008.12.030 [11] T. Huang, C. Li and X. Liao, Synchronization of a class of coupled chaotic delayed systems with parameter mismatch, Chaos, 2007, 17(3), 033121. doi: 10.1063/1.2776668 [12] T. Isokawa, T. Kusakabe, N. Matsui and F. Peper, Quaternion Neural Network and its Application, Springer, Berlin, Heidelberg, 2003. [13] I. Hussain, S. Jafari, D. Ghosh and M. Perc, Synchronization and chimeras in a network of photosensitive FitzHugh-Nagumo neurons, Nonlinear Dynam., 2021, 104, 2711–2721. doi: 10.1007/s11071-021-06427-x [14] A. Kumar, S. Das and Y. Joo, Quasi-projective synchronization of memristor-based complex valued recurrent neural network with time-varying delay and mismatched parameters, Neurocomputing, 2023, 559, 126774. doi: 10.1016/j.neucom.2023.126774 [15] H. Li, J. Cao, C. Hu, H. Jiang and F. Alsaadi, Synchronization analysis of discrete-time fractional-order quaternion-valued uncertain neural networks, IEEE Trans. Neural Netw. Learn. Syst., 2023. DOI: 10.1109/TNNLS.2023.3274959. [16] H. Li, B. Chen, Q. Zhou and S. Fang, Robust exponential stability for uncertain stochastic neural networks with discrete and distributed time-varying delays, Phys. Lett. A, 2008, 372(19), 3385–3394. doi: 10.1016/j.physleta.2008.01.060 [17] H. Li, C. Hu, J. Cao, H. Jiang and A. Alsaedi, Quasi-projective and complete synchronization of fractional-order complex-valued neural networks with time delays, Neural Networks, 2019, 118, 102–109. doi: 10.1016/j.neunet.2019.06.008 [18] R. Li, J. Cao, C. Xue and R. Manivannan, Quasi-stability and quasi-synchronization control of quaternion-valued fractional-order discrete-time memristive neural networks, Appl. Math. Comput., 2021, 395, 125851. [19] R. Li, X. Gao and J. Cao, Exponential synchronization of stochastic memristive neural networks with time-varying delays, Neural Process. Lett., 2019, 50(1), 459–475. doi: 10.1007/s11063-019-09989-5 [20] X. Li, D. Ding and D. Sang, Exponential stability of stochastic cellular neural networks with mixed delays, Commun. Stat. Theror. M., 2018, 47(19), 4881–4894. doi: 10.1080/03610926.2018.1459710 [21] X. Li, Q. Ma and X. Ding, Stochastic partitioned averaged vector field methods for stochastic differential equations with a conserved quantity, J. Appl. Anal. Comput., 2019, 9(5), 1663–1685. [22] Y. Li and C. Li, Matrix measure strategies for stabilization and synchronization of delayed bam neural networks, Nonlinear Dynam., 2016, 84(3), 1759–1770. doi: 10.1007/s11071-016-2603-x [23] X. Liao and X. Mao, Exponential stability and instability of stochastic neural networks, Stoch. Anal. Appl., 1996, 14(2), 165–185. doi: 10.1080/07362999608809432 [24] X. Liao and X. Mao, Stability of stochastic neural networks, Neural Parallel Sci. Comput., 1996, 4(2), 205–224. [25] G. Ling, M. Ge, X. Liu, G. Xiao and Q. Fan, Stochastic quasi-synchronization of heterogeneous delayed impulsive dynamical networks via single impulsive control, Neural Networks, 2021, 139, 223–236. doi: 10.1016/j.neunet.2021.03.011 [26] X. Liu, J. Cao and W. Yu, Filippov systems and quasi-synchronization control for switched networks, Chaos: An Interdisciplinary, J. Nonlinear Sci., 2012, 22(3), 033110. [27] Y. Liu, L. Sun, J. Lu and J. Liang, Feedback controller design for the synchronization of Boolean control networks, IEEE Trans. Neural Netw. Learn. Syst., 2016, 27(9), 1991–1996. doi: 10.1109/TNNLS.2015.2461012 [28] R. Mainieri and J. Rehacek, Projective synchronization in three-dimensional chaotic systems, Phys. Rev. Lett., 1999, 82(15), 3042. doi: 10.1103/PhysRevLett.82.3042 [29] N. Matsui, T. Isokawa, H. Kusamichi, F. Peper and H. Nishimura, Quaternion neural network with geometrical operators, J. Intell. Fuzzy Syst., 2004, 15(3–4), 149–164. [30] F. Parastesh, M. Mehrabbeik, R. Mahtab, K. Rajagopal, S. Jafari and M. Perc, Synchronization in Hindmarsh-Rose neurons subject to higher-order interactions, Chaos, 2022, 32(1), 013125. doi: 10.1063/5.0079834 [31] L. Pecora and T. Carrol, Synchronization in chaotic systems, Phys. Rev. Lett., 1990, 64(4), 821–824. [32] T. Peng, Y. Wu, Z. Tu, A. Alofi and J. Lu, Fixed-time and prescribed-time synchronization of quaternion-valued neural networks: A control strategy involving Lyapunov functions, Neural Networks, 2023, 160, 108–121. doi: 10.1016/j.neunet.2022.12.014 [33] F. Ren and J. Cao, Anti-synchronization of stochastic perturbed delayed chaotic neural networks, Neural Comput. App., 2009, 18(5), 515–521. doi: 10.1007/s00521-009-0251-5 [34] H. Shu, Q. Song, Y. Liu, Z. Zhao and F. Alsaadi, Global μ-stability of quaternion-valued neural networks with non-differentiable time-varying delays, Neurocomputing, 2017, 247, 202–212. doi: 10.1016/j.neucom.2017.03.052 [35] Q. Song, R. Zeng, Z. Zhao, Y. Liu and F. Alsaadi, Mean-square stability of stochastic quaternion-valued neural networks with variable coefficients and neutral delays, Neurocomputing, 2022, 471, 130–138. doi: 10.1016/j.neucom.2021.11.033 [36] Q. Song, Z. Zhao, Y. Liu and F. Alsaadi, Mean-square input-to-state stability for stochastic complex-valued neural networks with neutral delay, Neurocomputing, 2022, 470, 269–277. doi: 10.1016/j.neucom.2021.10.117 [37] X. Sun, M. Perc and J. Kurths, Effects of partial time delays on phase synchronization in Watts-Strogatz small-world neuronal networks, Chaos, 2017, 27(5), 053113. doi: 10.1063/1.4983838 [38] Z. Tu, J. Cao, A. Alsaedi and T. Hayat, Global dissipativity analysis for delayed quaternion-valued neural networks, Neural Networks, 2017, 89, 97–104. doi: 10.1016/j.neunet.2017.01.006 [39] L. Wan and Q. Zhou, Attractor and ultimate boundedness for stochastic cellular neural networks with delays, Nonlinear Anal-Real., 2011, 12(5), 2561–2566. doi: 10.1016/j.nonrwa.2011.03.005 [40] R. Wang, Z. Zhang, J. Qu and J. Cao, Phase synchronization motion and neural coding in dynamic transmission of neural information, IEEE T. Neural Networ., 2011, 22(7), 1097–1106. doi: 10.1109/TNN.2011.2119377 [41] Y. Wang, J. Lu, J. Liang, J. Cao and M. Perc, Pinning synchronization of nonlinear coupled Lur'e networks dnder hybrid impulses, IEEE T. Circuits-Ⅱ, 2019, 66(3), 432–436. [42] Z. Wang, S. Lauria and X. Liu, Exponential stability of uncertain stochastic neural networks with mixed time-delays, Chaos Solition Fract., 2007, 32(1), 62–72. doi: 10.1016/j.chaos.2005.10.061 [43] H. Wei, B. Wu and R. Li, Synchronization control of quaternion-valued neural networks with parameter uncertainties, Neural Process. Lett., 2019, 1–20. [44] R. Wei and J. Cao, Fixed-time synchronization of quaternion-valued memristive neural networks with time delays, Neural Networks, 2019, 113, 1–10. doi: 10.1016/j.neunet.2019.01.014 [45] R. Wei and J. Cao, Synchronization control of quaternion-valued memristive neural networks with and without event-triggered scheme, Cogn. Neurodynamics, 2019, 13(5), 489–502. doi: 10.1007/s11571-019-09545-w [46] Z. Wu and X. Gong, Impulsive synchronization of time-varying dynamical network, J. Appl. Anal. Comput., 2016, 6(1), 94–102. [47] X. Yang, J. Cao, Y. Long and W. Rui, Adaptive lag synchronization for competitive neural networks with mixed delays and uncertain hybrid perturbations, IEEE T. Neural Networ., 2010, 21(10), 1656–1667. doi: 10.1109/TNN.2010.2068560 [48] T. Zhang and Z. Li, Switching clusters' synchronization for discrete space-time complex dynamical networks via boundary feedback controls, Pattern Recogn., 2023, 143C, 109763. -
-
-
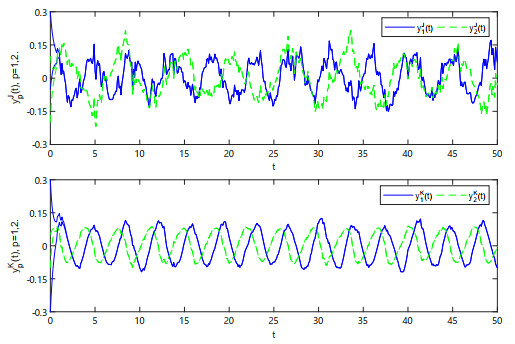
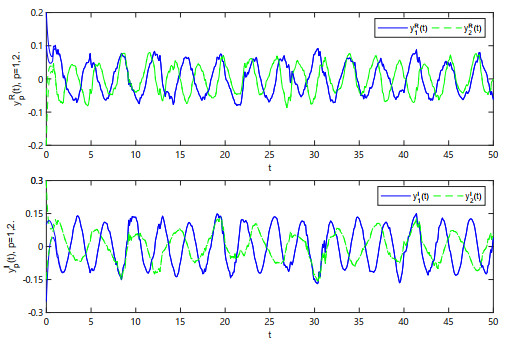
Figure 1.
The trajectories of drive system states
$ y_{p}^{R} $ $ y_{p}^{I} $ $ p=1,2 $ -
Figure 2.
The trajectories of drive system states
$ y_{p}^{J} $ $ y_{p}^{K} $ $ p=1,2 $ -
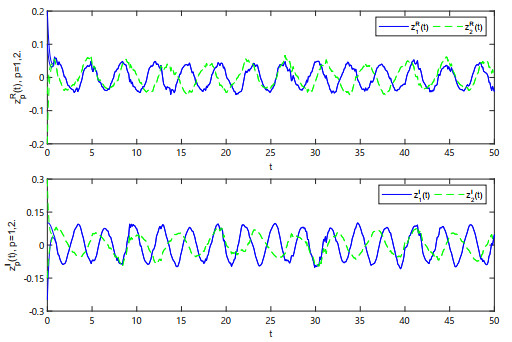
Figure 3.
The trajectories of response system states
$ z_{p}^{R} $ $ z_{p}^{I} $ $ p=1,2 $ -
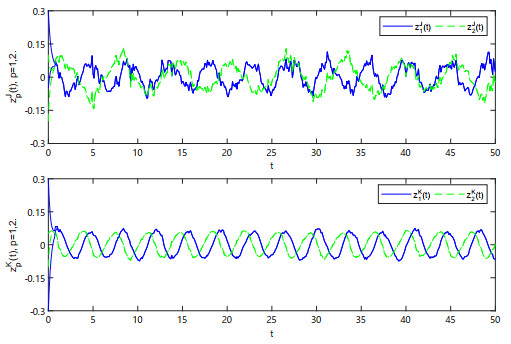
Figure 4.
The trajectories of response system states
$ z_{p}^{J} $ $ z_{p}^{K} $ $ p=1,2 $ -
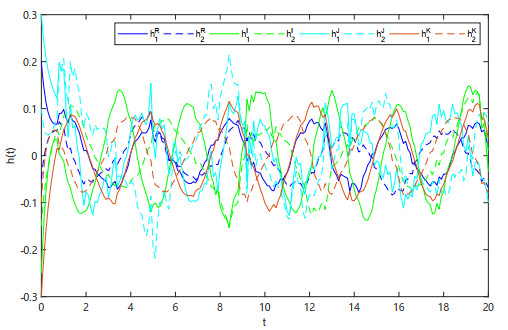
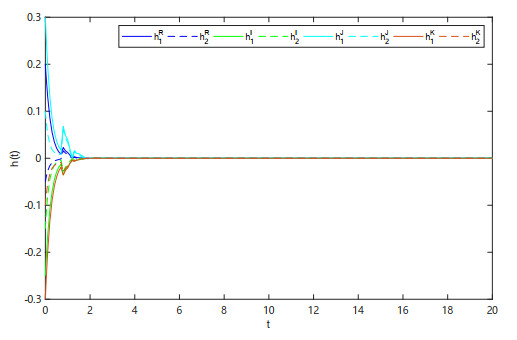
Figure 5.
The evolution curves of quasi-projective synchronization error
$ h(t) $ $ E_p(t) $ -
Figure 6.
The evolution curves of quasi-projective synchronization error
$ h(t) $ $ E_p(t) $




 DownLoad:
DownLoad: