| Citation: | Binbin Du, Changjian Wu, Guang Zhang, Xiao-Liang Zhou. DYNAMICAL BEHAVIORS OF A DISCRETE TWO-DIMENSIONAL COMPETITIVE SYSTEM EXACTLY DRIVEN BY THE LARGE CENTRE[J]. Journal of Applied Analysis & Computation, 2024, 14(5): 2822-2844. doi: 10.11948/20230437 |
DYNAMICAL BEHAVIORS OF A DISCRETE TWO-DIMENSIONAL COMPETITIVE SYSTEM EXACTLY DRIVEN BY THE LARGE CENTRE
-
Abstract
In this paper, a new discrete large-sub-center system is obtained by using the Euler and nonstandard discretization methods for the corresponding continuous system. It is surprised that all dynamic behaviors of the discrete system are exactly driven by the large-center equation, for example, the stabilities, the bifurcations, the period-doubling orbits, and the chaotic dynamics, etc. Additionally, the global asymptotical stability, the existence of exact 2-periodic solutions, the flip bifurcation theorem, and the invariant set of the sub-center equation is also given. These results reveal far richer dynamics of the discrete model compared with the continuous model. Through numerical simulation, we can observe some complex dynamic behaviors, such as period-doubling cascade, periodic windows, chaotic dynamics, etc. Especially, our theoretical results are also showed by those numerical simulations.
-
Keywords:
- Large-sub-center /
- discrete system /
- flip bifurcation /
- center manifold method /
- chaos
-

-
References
[1] S. Akhtar, R. Ahmed, M. Batool, N. A. Shah and J. D. Chung, Stability, bifurcation and chaos control of a discretized Leslie prey-predator model, Chaos, Solitons and Fractals, 2021, 152, 111345. doi: 10.1016/j.chaos.2021.111345 [2] S. S. Askar, A competition of duopoly game whose players are public: Dynamic investigations, Communications in Nonlinear Science and Numerical Simulation, 2022, 111, 106486. doi: 10.1016/j.cnsns.2022.106486 [3] G. L. Baker and J. P. Gollub, Chaotic Dynamics: An Introduction, Cambridge University Press, Cambridge, 1990. [4] W. J. Baumol and J. Benhabib, Chaos: Significance, mechanism and economic applications, Journal of Economic Perspectives, 1989, 3(1), 77–105. doi: 10.1257/jep.3.1.77 [5] M. Biswas and N. Bairagi, On the dynamic consistency of a two-species competitive discrete system with toxicity: Local and global analysis, Journal of Computational and Applied Mathematics, 2020, 363, 145–155. doi: 10.1016/j.cam.2019.06.005 [6] V. Cafagna and P. Coccorese, Dynamical systems and the arising of cooperation in a Cournot duopoly, Chaos, Solitons and Fractals, 2005, 25(3), 655–664. doi: 10.1016/j.chaos.2004.11.051 [7] D. M. Chan and J. E. Franke, Probabilities of extinction, weak extinction, permanence, and mutual exclusion in discrete, competitive, Lotka-Volterra systems that involve lnvading species, Mathematical and Computer Modelling, 40, 2004, 809–821. doi: 10.1016/j.mcm.2004.10.013 [8] J. Chen, Y. Chen, Z. Zhu and F. Chen, Stability and bifurcation of a discrete predator-prey system with Allee effect and other food resource for the predators, Journal of Applied Mathematics and Computing, 2023, 69(1), 529–548. doi: 10.1007/s12190-022-01764-5 [9] C. Damgaard, Dynamics in a discrete two-species competition model: Coexistence and over-compensation, Journal of Theoretical Biology, 2004, 227, 197–203. doi: 10.1016/j.jtbi.2003.11.001 [10] H. Dawid, M. Y. Keoula, M. Kopel and P. M. Kort, Dynamic investment strategies and leadership in product innovation, European Journal of Operational Research, 2023, 306(1), 431–447. doi: 10.1016/j.ejor.2022.06.046 [11] Z. W. Ding and G. P. Shi, Cooperation in a dynamical adjustment of duopoly game with incomplete information, Chaos, Solitons and Fractals, 2009, 40(2), 989–993. [12] M. Frank and T. Stengos, Chaotic dynamics in economic time-series, Journal of Economic Surveys, 1988, 2(2), 103–133. doi: 10.1111/j.1467-6419.1988.tb00039.x [13] K. Gopalsamy, Stability and Oscillations in Delay Differential Equations of Population Dynamics, Kluwer Academic Publishers, Dordrecht, 1992. [14] J. Guckenheimer and P. Holmes, Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields, Springer, New York, 1983. [15] J. Guckenheomer, G. Oster and A. Ipaktchi, The dynamics of density dependent population models, J. Math. Biology, 1977, 4, 101–147. doi: 10.1007/BF00275980 [16] X. L. Han and C. Y. Lei, Bifurcation and turing instability analysis for a space- and time-discrete predator–prey system with Smith growth function, Chaos, Solitons and Fractals, 2023, 166, 112910. doi: 10.1016/j.chaos.2022.112910 [17] Y. Huang, The Marotto theorem on planar monotone or competitive maps, Chaos, Solitons and Fractals, 2004, 19, 1105–1112. doi: 10.1016/S0960-0779(03)00283-2 [18] H. Jiang and T. D. Rogers, The discrete dynamics of symmetric competition in the plane, Journal of Mathematical Biology, 1987, 25, 573–596. doi: 10.1007/BF00275495 [19] X. Jin and X. Y. Li, Dynamics of a discrete two-species competitive model with Michaelies-Menten type harvesting in the first species, Journal of Nonlinear Modeling and Analysis, 2023, 5(3), 494–523. [20] Y. Kang, Pre-images of invariant sets of a discrete-time two-species competition model, Journal of Difference Equations and Applications, 2012, 18(10), 1709–1733. doi: 10.1080/10236198.2011.591390 [21] Y. Kang and H. Smith, Global dynamics of a discrete two-species Lottery-Ricker competition model, Journal of Biological Dynamics, 2012, 6(2), 358–376. doi: 10.1080/17513758.2011.586064 [22] D. Kelsey, The economics of chaos or the chaos of economics?, Oxford Economic Papers, 1988, 40, 1–3. doi: 10.1093/oxfordjournals.oep.a041839 [23] A. Q. Khan, Bifurcation analysis of a discrete-time two-species model, Discrete Dynamics in Nature and Society, 2020, 2020, Article ID 2954059, 12 pp. [24] A. Q. Khan, J. Y. Ma and D. M. Xiao, Bifurcations of a two-dimensional discrete time plant-herbivore system, Communications in Nonlinear Science and Numerical Simulation, 2016, 39, 185–198. doi: 10.1016/j.cnsns.2016.02.037 [25] M. S. Khan, M. Samreen, J. F. Gómez-Aguilar and E. Pérez-Careta, On the qualitative study of a discrete-time phytoplankton-zooplankton model under the effects of external toxicity in phytoplankton population, Heliyon, 2022, 8, e12415. doi: 10.1016/j.heliyon.2022.e12415 [26] Y. Kuang, Delay Differential Equations with Applications in Population Dynamics, Academic Press, New York, 1993. [27] M. S. Li and X. L. Zhou, Dynamic properties of a discrete population model with diffusion, Advances in Difference Equations, 2020, 2020, 580, DOI: 10.1186/s13662-020-03033-w. [28] T. Y. Li and J. A. Yorke, Period three implies chaos, American Mathematical Monthly, 1975, 82(10), 985–992. doi: 10.1080/00029890.1975.11994008 [29] X. Li and Y. Liu, Transcritical bifurcation and flip bifurcation of a new discrete ratio-dependent predator-prey system, Qualitative Theory of Dynamical Systems, 2022, 21, 122, DOI: 10.1007/s12346-022-00646-2. [30] X. Liang and J. F. Jiang, On the topological entropy, nonwandering set and chaos of monotone and competitive dynamical systems, Chaos, Solitons and Fractals, 14(2002), 689–696. doi: 10.1016/S0960-0779(02)00013-9 [31] P. Z. Liu and S. N. Elaydi, Discrete competitive and cooperative Lotka–Volterra type, J. Computational Analysis and Applications, 2001, 3(1), 53–73. doi: 10.1023/A:1011539901001 [32] X. L. Liu and D. M. Xiao, Complex dynamic behaviors of a discrete-time predator-prey system, Chaos, Solitons and Fractals, 32(2007), 80–94. doi: 10.1016/j.chaos.2005.10.081 [33] F. R. Marotto, Snap-back repellers imply chaos in $\mathbb{R}^{n}$, J. Math. Anal. Appl., 1978, 63(1), 199–223. doi: 10.1016/0022-247X(78)90115-4 [34] F. R. Marotto, On redefining a snap-back repeller, Chaos, Solitons and Fractals, 2005, 25, 25–28. doi: 10.1016/j.chaos.2004.10.003 [35] R. M. May, Simple mathematical models with very complicated dynamics, Nature, 1976, 261, 459–467. doi: 10.1038/261459a0 [36] R. E. Mickens, Genesis of elementary numerical instabilities in finite-difference models of ordinary differential equations, in: G. S. Ladde, M. Sambandham (Ed. ), Proceedings of Dynamics Systems and Applications, Dynamics publisher, USA. 1994, 1, 251–258. [37] P. Nijkamp and A. Reggiani, Spatial competition and ecologically based socioeconomic models, Socio-Spatial Dynamics, 1992, 3(2), 89–109. [38] P. Nijkamp and A. Reggiani, Space-Time Dynamics, Spatial Competition and the Theory of Chaos, Structure and Change in the Space-Economv (T. R. Lakshmanan and P. Nijkamp, eds. ), Springer, Berlin, 1993. [39] P. Nijkamp and A. Reggiani, Non-linear evolution of dynamic spatial systems: The relevance of chaos and ecologically-based models, Regional Science and Urban Economics, 1995, 25, 183–210. doi: 10.1016/0166-0462(94)02077-T [40] R. M. Nisbet and L. C. Onyiah, Population dynamic consequences of competition within and between age classes, Journal of Mathematical Biology, 1994, 32, 329–344. doi: 10.1007/BF00160164 [41] L. R. Ricardo and F. P. Danièle, Periodic and chaotic events in a discrete model of logistic type for the competitive interaction of two species, Chaos, Solitons & Fractals, 2009, 41(1), 334–347. [42] S. Rocklin and G. Oster, Competition between Phenotypes, Journal of Mathematical Biology, 1976, 3, 225–261. doi: 10.1007/BF00275058 [43] A. N. Sharkovskii, Coexistence of cycles of a continuous mapping of the line into itself, Ukrainian Math. J., 1964, 16, 61–71. [44] A. N. Sharkovskii, Coexistence of cycles of a continuous mapping of the line into itself, International J. Bifurcation and Chaos, 1995, 5(5), 1263–1273(which is translated by J. Tolosa). doi: 10.1142/S0218127495000934 [45] A. N. Sharkovsky, S. F. Kolyada, A. G. Sivak and V. V. Fedorenko, Dynamies of One-Dimensional Maps, Naukova Dumka, Kiev, 1989. [46] C. W. Shih and J. P. Tseng, Global consensus for discrete-time competitive systems, Chaos, Solitons & Fractals, 2009, 41(1), 302–310. [47] A. Voroshilova and J. Wafubwa, Discrete competitive Lotka–Volterra model with controllable phase volume, Systems, 2020, 8, 17. DOI: 10.3390/systems8020017. [48] W. B. Yao and X. Y. Li, Bifurcation difference induced by different discrete methods in a discrete predator-prey model, Journal of Nonlinear Modeling and Analysis, 2022, 4(1), 64–79. [49] K. Yuan and J. D. Cao, Periodic oscillatory solution in delayed competitive–cooperative neural networks: A decomposition approach, Chaos, Solitons & Fractals, 2006, 27(1), 223–231. [50] L. G. Yuan and Q. G. Yang, Bifurcation, invariant curve and hybrid control in a discrete-time predator-prey system, Appl. Math. Model., 2015, 39, 2345–2362. doi: 10.1016/j.apm.2014.10.040 [51] G. Zhang, D. M. Jiang and S. S. Cheng, 3-periodic traveling wave solutions for a dynamical coupled map lattice, Nonlinear Dyn., 2007, 50, 235–247. doi: 10.1007/s11071-006-9154-5 -
-
-
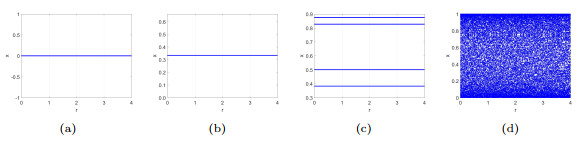
Figure 1.
The phase diagrams of (1.4) for
$ a=0.5,1.5,3.5,4 $ -
Figure 2.
The bifurcation diagrams of the second equation of (1.1) for
$ b=0.01 $ $ a=0.5,1.5,3.5,4 $ -
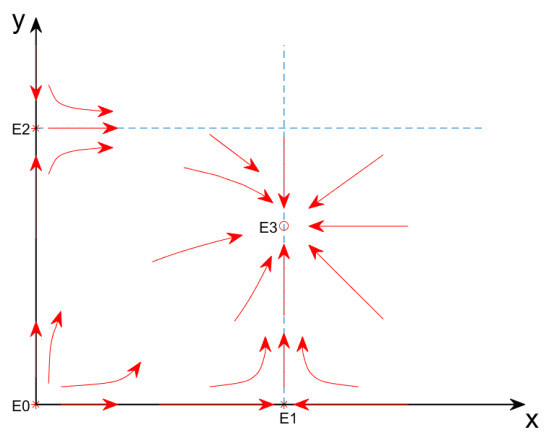
Figure 3.
The local phase diagrams of (1.7) for
$ 1<a<3 $ -
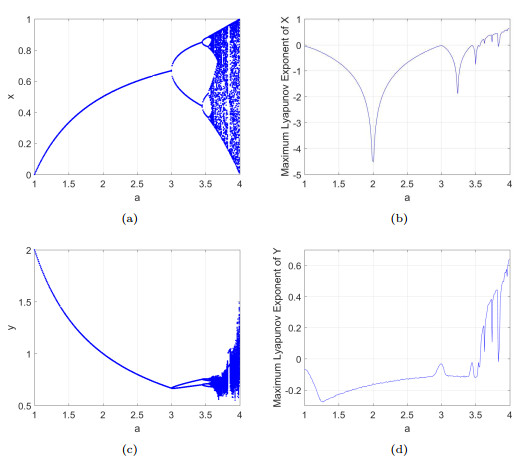
Figure 4.
$ b=c=0.5 $ $ a\in \left( 1,4\right) $ -
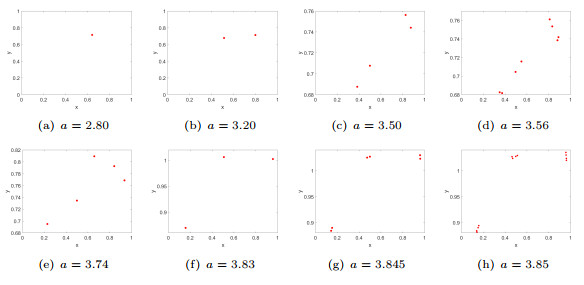
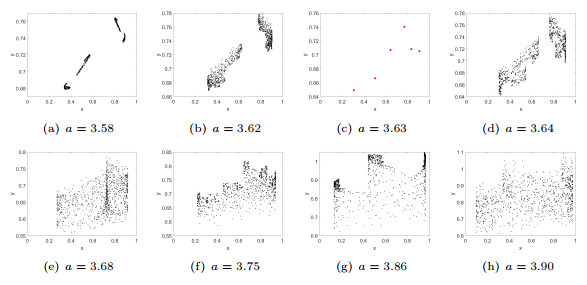
Figure 5.
Different choices at
$ a\in \left(1,4\right) $ -
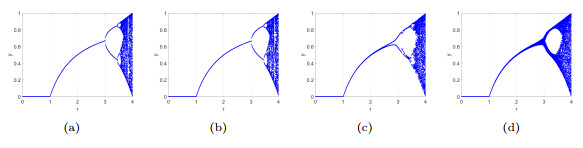
Figure 6.
Different choices at
$ a\in \left(1,4\right) $ -
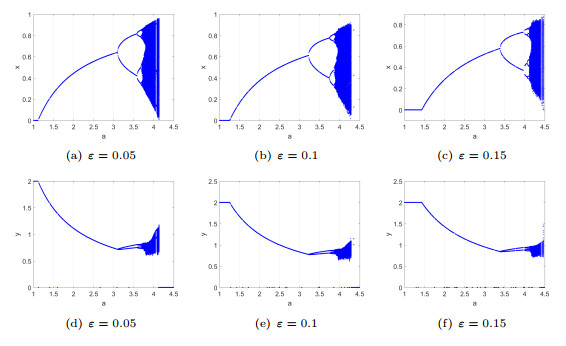
Figure 7.
$ b=c=0.5 $ $ a\in \left[1,4.5\right] $




 DownLoad:
DownLoad: