| Citation: |
Fuchen Zhang, Song Chen, Xiusu Chen, Jinde Cao, Fei Xu. SYNCHRONIZATION OF A NOVEL COMPLEX SYSTEM[J]. Journal of Applied Analysis & Computation, 2025, 15(5): 2508-2527. doi: 10.11948/20240020
|
SYNCHRONIZATION OF A NOVEL COMPLEX SYSTEM
-
Abstract
In this paper, we introduce a new hyperchaotic system which is a four-dimensional system of nonlinear differential equations. This system exhibits very rich chaotic dynamical behaviors. The dynamical characteristics of this system are analysed theoretically and numerically, including the dissipation, the quilibrium points and their stability, Lyapunov exponents, the Lyapunov dimension of the attractors, the global exponential attractive set. In order to achieve synchronization fast, global exponential synchronization is adopted. Suitable linear and nonlinear controllers have been designed to achieve global exponential synchronization between two identical chaotic systems by using the Lyapunov stability theory and Dini derivative. The innovation of this paper is that firstly we get the globally exponential attractive set of this system. Secondly, the result of globally exponential attractive set of the chaotic system is applied to chaos synchronization. Thirdly, we can get the precise lower bound of the coefficient of linear feedback controller ${k_1}, {k_2}, {k_3}$ and ${k_4}$. Finally, chaos synchronization is studied numerically. Numerical simulations are in excellent agreement with the theoretical study.
-
-
References
[1] M. P. Asir, K. Thamilmaran, A. Prasad, U. Feudel, N. V. Kuznetsov and M. D. Shrimali, Hidden strange nonchaotic dynamics in a non-autonomous model, Chaos Soliton. Fract., 2023, 168, 113101. doi: 10.1016/j.chaos.2023.113101 [2] G. Chen and T. Ueta, Yet another chaotic attractor, Int. J. Bifurc. Chaos Appl. Sci. Eng., 1999, 9, 1465-1466. doi: 10.1142/S0218127499001024 [3] L. Chua, M. Komuro and T. Matsumoto, The double scroll family, IEEE Trans. Circuits Syst., 1986, 33(11), 1072-1118. doi: 10.1109/TCS.1986.1085869 [4] Z. Y. Dong, X. Wang, X. Zhang, M. Hu and T. N. Dinh, Global exponential synchronization of discrete-time high-order switched neural networks and its application to multi-channel audio encryption, Nonlinear Anal. -Hybri., 2023, 47, 101291. doi: 10.1016/j.nahs.2022.101291 [5] P. Frederickson, J. Kaplan, E. Yorke and J. Yorke, The Lyapunov dimension of strange attractors, J. Differ. Equ., 1983, 49(2), 185-207. doi: 10.1016/0022-0396(83)90011-6 [6] D. Khattar, N. Agrawal and G. Singh, Chaos synchronization of a new chaotic system having exponential term via adaptive and sliding mode control, Differ. Equ. Dyn. Syst., 2023, 1-19. https//doi. org/10.1007/s12591-023-00635-0. [7] D. H. Kobe, Helmholtz's theorem revisited, Am J Phys. 1986, 54(6), 552-554. doi: 10.1119/1.14562 [8] N. Kuznetsov, T. Mokaev, O. Kuznetsova and E. V. Kudryashova, The Lorenz system: Hidden bounary of practical stability and the Lyapunov dimension, Nonlinear Dyn., 2020, 102, 713-732. doi: 10.1007/s11071-020-05856-4 [9] N. Kuznetsov, T. Mokaev, V. Ponomarenko, E. Seleznev, N. Stankevich and L. Chua, Hidden attractors in Chua circuit: Mathematical theory meets physical experiments, Nonlinear Dyn., 2023, 111(6), 5859-5887. doi: 10.1007/s11071-022-08078-y [10] G. A. Leonov, Lyapunov functions in the attractors dimension theory, J. Appl. Math. Mech., 2012, 76(2), 129-141. doi: 10.1016/j.jappmathmech.2012.05.002 [11] G. A. Leonov and V. A. Boichenko, Lyapunov's direct method in the estimation of the Hausdorff dimension of attractors, Acta Appl. Math., 1992, 26(1), 1-60. doi: 10.1007/BF00046607 [12] G. A. Leonov and N. V. Kuznetsov, Time-varying linearization and the Perron effects, Int. J. Bifurc. Chaos Appl. Sci. Eng., 2007, 17(4), 1079-1107. doi: 10.1142/S0218127407017732 [13] T. Y. Li and J. A. Yorke, Period three implies chaos, Am. Math. Mon., 1975, 82, 985-992. doi: 10.1080/00029890.1975.11994008 [14] M. Liu, J. Liu, J. Liang, Y. Sun and Y. Shu, Observer-based secure synchronization control of directed complex-valued dynamical networks under link attacks, Nonlinear Dyn., 2024, 112, 12303-12318. doi: 10.1007/s11071-024-09695-5 [15] R. Liu, H. Liu and M. Zhao, Reveal the correlation between randomness and Lyapunov exponent of n-dimensional non-degenerate hyper chaotic map, Integration, 2023, 93, 102071. doi: 10.1016/j.vlsi.2023.102071 [16] E. N. Lorenz, Deterministic nonperiodic flow, J. Atmos. Sci., 1963, 20, 130-141. doi: 10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2 [17] J. Lu and G. Chen, A new chaotic attractor coined, Int. J. Bifurc. Chaos Appl. Sci. Eng., 2002, 12(3), 659-661. doi: 10.1142/S0218127402004620 [18] J. Lu, G. Chen, D. Cheng and S. Celikovsky, Bridge the gap between the Lorenz system and the Chen system, Int. J. Bifurcat. Chaos., 2002, 12(12), 2917-2926. doi: 10.1142/S021812740200631X [19] G. M. Mahmoud, M. A. Al-Kashif and A. A. Farghaly, Chaotic and hyperchaotic attractors of a complex nonlinear system, J. Phys. A: Math. Theor., 2008, 41(5), 055104. doi: 10.1088/1751-8113/41/5/055104 [20] Z. T. Njitacke, C. N. Takembo, J. Awrejcewicz, H. P. E. Fouda and J. Kengne, Hamilton energy, complex dynamical analysis and information patterns of a new memristive FitzHugh-Nagumo neural network, Chaos Soliton. Fract., 2022, 160, 112211. doi: 10.1016/j.chaos.2022.112211 [21] E. Ott, C. Grebogi and J. A. Yorke, Controlling chaos, Phys. Rev. Lett., 1990, 64(11), 1196-1199. doi: 10.1103/PhysRevLett.64.1196 [22] J. Park, H. Lee and J. Baik, Periodic and chaotic dynamics of the Ehrhard-Muller system, Int. J. Bifurc. Chaos Appl. Sci. Eng., 2016, 26(6), 1630015. doi: 10.1142/S0218127416300159 [23] L. M. Pecora and T. L. Carroll, Synchronization in chaotic systems, Phys. Rev. Lett., 1990, 64(8), 821-824. doi: 10.1103/PhysRevLett.64.821 [24] H. Poincaré, Sur le probleme des trois corps et les equations de la dynamique, Acta Math., 1890, 13, 1-270. doi: 10.1007/BF02392514 [25] O. E. Rossler, An equation for continuous chaos, Phys. Lett. A, 1976, 57, 397-398. doi: 10.1016/0375-9601(76)90101-8 [26] C. Sarasola, F. J. Torrealdea, A. Anjou, A. Moujahid and M. Grana, Energy balance in feedback synchronization of chaotic systems, Phys. Rev. E, 2004, 69(1), 011606. doi: 10.1103/PhysRevE.69.011606 [27] C. Sparrow, The Lorenz Equations: Bifurcations, Chaos and Strange Attractors, Applied Mathematical Science, vol. 41, Springer, New York, 1982. [28] L. Stenflo, Generalized Lorenz equations for acoustic-gravity waves in the atmosphere, Phys. Scr., 1996, 3, 83-84. [29] J. C. Vallejo and M. A. Sanjuan, Predictability of Chaotic Dynamics, A Finite-Time Lyapunov Exponents Approach, Springer, Cham, 2019. [30] A. Wagemakers, A. Hartikainen, A. Daza, E Rasanen and M. A. Sanjuan, Chaotic dynamics creates and destroys branched flow, Phys. Rev. E, 2025, 111(1), 014214. doi: 10.1103/PhysRevE.111.014214 [31] A. Wolf, J. B. Swift, H. L. Swinney and J. A. Vastano, Determining Lyapunov exponents from a time series, Physica D., 1985, 16, 285-317. doi: 10.1016/0167-2789(85)90011-9 [32] F. C. Zhang and F. Xu, Dynamical behavior of the generzlized complex Lorenz chaotic system, J. Appl. Anal. Comp., 2024, 14(4), 1915-1931. [33] F. C. Zhang, F. Xu and X. Zhang, Qualitative behaviors of a four-dimensional Lorenz system, J. Phys. A: Math. Theor., 2024, 57(9), 095201. doi: 10.1088/1751-8121/ad26ac [34] F. C. Zhang and G. Y. Zhang, Further results on ultimate bound on the trajectories of the Lorenz system, Qual. Theory Dyn. Syst., 2016, 15(1), 221-235. doi: 10.1007/s12346-015-0137-0 [35] F. C. Zhang, P. Zhou and F. Xu, Qualitative properties of a physically extended six-dimensional Lorenz system, Int. J. Bifurc. Chaos Appl. Sci. Eng., 2024, 34(7), 2450083. doi: 10.1142/S0218127424500834 [36] F. F. Zhang, W. Liu, L. Wu and J. Li, Chaotic model and control of an atmospheric convective system coupled with large-scale circulation, Phys. Scr., 2024, 99(4), 045213. doi: 10.1088/1402-4896/ad2bc1 [37] X. T. Zhang, J. Liu, J. C. Liang, D. Wang and Y. Sun, Chaos anti-control of coexisting infinite signals and pinning synchronization of a complex-valued laser chain network, Eur. Phys. J. Plus, 2024, 139(65), 1-14. doi: 10.1140/epjp/s13360-023-04826-0 [38] J. Zuo, J. Zhang, X. Wei, L. Yang, N. Cheng and J. Lu, Design and application of multisroll conservative chaotic system with no equilibrium, dynamics analysis, circuit implementation, Chaos Soliton. Fract., 2024, 187, 115331. doi: 10.1016/j.chaos.2024.115331 -
-
Figures(8)
Export File
Citation
Fuchen Zhang, Song Chen, Xiusu Chen, Jinde Cao, Fei Xu. SYNCHRONIZATION OF A NOVEL COMPLEX SYSTEM[J]. Journal of Applied Analysis & Computation, 2025, 15(5): 2508-2527. doi: 10.11948/20240020
Format
Content
DownLoad:
-
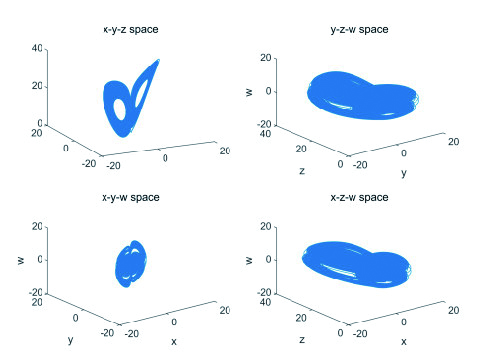
Figure 1.
The hyperchaotic attractors of system (2.2) in the 3D space
-
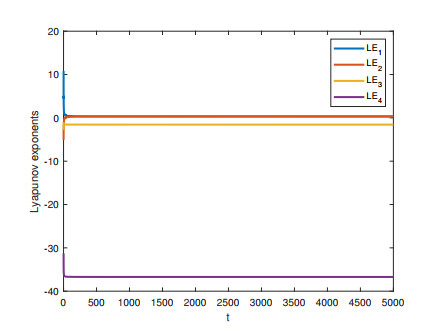
Figure 2.
The Lyapunov exponent chart of system (2.2)
-
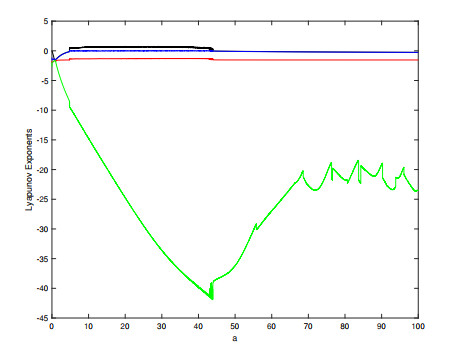
Figure 3.
Lyapunov exponents diagram of system with
$ a \in \left[ {0, 100} \right] $ -
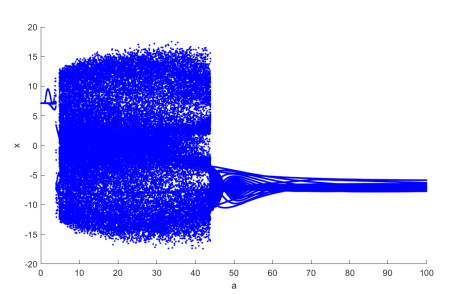
Figure 4.
Bifurcation diagram of state variable
$ x $ $ a $ -
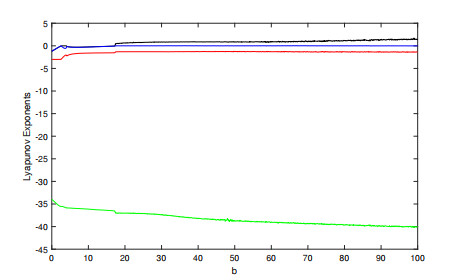
Figure 5.
Lyapunov exponents diagram of system (2.2) with
$ b \in [0, 100]. $ -
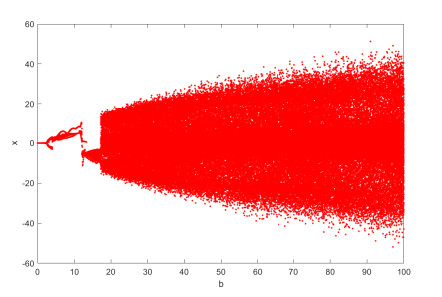
Figure 6.
Bifurcation diagram of state variable
$ x $ $ b $ -
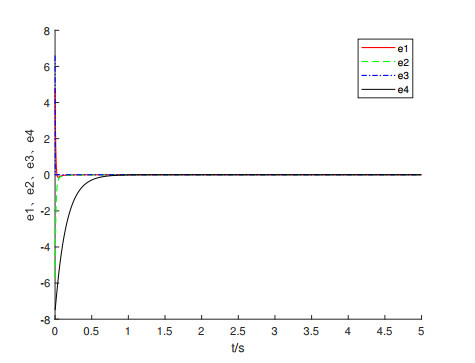
Figure 7.
Synchronization error of linear feedback control is illustrated when
$ {k_1} = 38, {k_2} = 72, {k_3} = 5160, {k_4} = 5. $ -
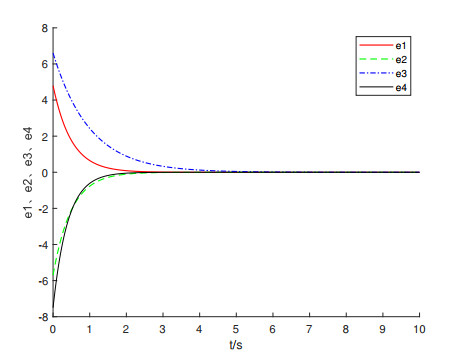
Figure 8.
Synchronization error of nonlinear feedback control is illustrated when
$ {l_1} = - 33, {l_2} = 1, {l_3} = - 1, {l_4} = 1. $