| Citation: | Bashir Nawaz, Kifayat Ullah, Hasanen A. Hammad, Manuel De la Sen. POLYNOMIOGRAPHS AND CONVERGENCE: A COMPARATIVE STUDY OF ITERATION PROCESSES UNDER KANANN-SUZUKI-(C) CONDITION[J]. Journal of Applied Analysis & Computation, 2025, 15(5): 2528-2550. doi: 10.11948/20240236 |
POLYNOMIOGRAPHS AND CONVERGENCE: A COMPARATIVE STUDY OF ITERATION PROCESSES UNDER KANANN-SUZUKI-(C) CONDITION
-
Abstract
In this paper, we study generalized ($C$)-conditions, specifically the Kannan-Suzuki-($C$) condition (abbreviated as the (KSC)-condition). We employ the M-iteration process to investigate the convergence behavior of mappings satisfying the KSC-condition and demonstrate that this approach offers improved convergence speed and computational efficiency compared to other well-known iteration schemes in the literature. To illustrate the advantages of the M-iteration process, we present new numerical examples that highlight its effectiveness. Additionally, we validate our theoretical findings by applying the method to fractional delay differential equations, showcasing its applicability in solving complex mathematical models. Furthermore, we compare the polynomiographs generated by the M-iteration process with those produced by other well-known iteration methods, demonstrating superior visualization properties and computational performance. These results establish the M-iteration process as a powerful tool for studying generalized contraction conditions.
-
Keywords:
- M-iteration /
- (KSC)-condition /
- fixed point /
- polynomiography /
- convergence /
- numerical method /
- iterative method
-

-
References
[1] M. Abbas, M. W. Asghar and M. De la Sen, Approximation of the solution of delay fractional differential equation using AA-Iterative scheme Mathematics, 2022, 10(2), 273. doi: 10.3390/math10020273 [2] R. Agarwal, D. O'Regan and D. Sahu, Iterative construction of fixed points of nearly asymptotically nonexpansive mappings Journal of Nonlinear and Convex Analysis, 2007, 8(1), 61-79. [3] G. Ardelean, Generating the basins of attraction for Newton's method Creative Math. and Inf, 2008, 17, 285-292. [4] A. Babakhani, D. Baleanu and R. P. Agarwal, Research Article the Existence and Uniqueness of Solutions for a Class of Nonlinear Fractional Differential Equations with Infinite Delay 2013. [5] D. Baleanu, F. Jarad, et al., Existence and uniqueness theorem for a class of delay differential equations with left and right caputo fractional derivatives Journal of Mathematical Physics, 2008, 49(8). [6] S. Banach, Sur les opérations dans les ensembles abstaits et leur application aux équations intégrales Fundamenta Mathematicae, 1922, 3(1), 133-181. [7] F. Browder, Nonexpansive nonlinear operators in a Banach space, Proceedings of the National Academy of Sciences of the United States of America, 1965, 54(4), 1041-1044. [8] P. Chuadchawna, A. Farajzadeh and A. Kaewcharoen, Convergence theorems and approximating endpoints for multivalued Suzuki mappings in hyperbolic spaces, Journal of Computational Analysis & Applications, 2020, 28(5). [9] K. Goebel and W. Kirk, Topics in Metric Fixed Point Theory, Cambridge University Press, Cambridge, 1990. [10] D. Göhde, Zum Prinzip der kontraktiven Abbildung, Mathematische Nachrichten, 1965, 30(3-4), 251-258. [11] I. Gościniak and K. Gdawiec, Control of dynamics of the modified Newton-Raphson algorithm, Communications in Nonlinear Science and Numerical Simulation, 2019, 67, 76-99. doi: 10.1016/j.cnsns.2018.07.010 [12] H. A. Hammad, H. ur Rehman and M. De la Sen, Advanced algorithms and common solutions to variational inequalities, Symmetry, 2020, 12(7), 1198. [13] H. A. Hammad and M. De la Sen, Stability and controllability study for mixed integral fractional delay dynamic systems endowed with impulsive effects on time scales Fractal and Fractional, 2023, 7(1), 92. doi: 10.3390/fractalfract7010092 [14] H. A. Hammad and M. De la Sen, A tripled fixed point technique for solving a tripled-system of integral equations and Markov process in CCbMS, Advances in Difference Equations, 2020, 567, 2020. [15] B. Kalantari, Polynomiography: From the fundamental theorem of algebra to art Leonardo, 2005, 38(3), 233-238. doi: 10.1162/0024094054029010 [16] E. Karapınar and K. Taş, Generalized (C)-conditions and related fixed point theorems Computers & Mathematics with Applications, 2011, 61(11), 3370-3380. [17] S. H. Khan, A Picard-Mann hybrid iterative process, Fixed Point Theory and Applications, 2013, 2013(1), 1-10. doi: 10.1186/1687-1812-2013-1 [18] A. Kilbas and S. Marzan, Cauchy problem for differential equation with caputo derivative Fractional Calculus and Applied Analysis, 2004, 7(3), 297-321. [19] W. Kirk, A fixed point theorem for mappings which do not increase distances the American Mathematical Monthly, 1965, 72(9), 1004-1006. [20] M. A. Krasnosel'skii, Two remarks on the method of successive approximations Uspekhi Matematicheskikh Nauk, 1955, 10(1), 123-127. [21] F. Mainardi, Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models World Scientific, 2022. [22] W. Mann, Mean value methods in iteration, Proceedings of the American Mathematical Society, 1953, 4(3), 506-510. [23] B. Mensour and A. Longtin, Chaos control in multistable delay-differential equations and their singular limit maps Physical Review E, 1998, 58(1), 410. [24] K. Miller, An Introduction to the Fractional Calculus and Fractional Differential Equations John Willey & Sons, 1993. [25] B. Nawaz, K. Ullah and K. Gdawiec, Convergence analysis of Picard-SP iteration process for generalized α-nonexpansive mappings Numerical Algorithms, 2024, 1-22. [26] B. Nawaz, K. Ullah and K. Gdawiec, Convergence analysis of a Picard-CR iteration process for nonexpansive mappings Soft Computing, 2025. [27] B. Nawaz, K. Ullah and M. Noorwali, Polynomiograph comparison and stability of a new iteration process International Journal of Analysis and Applications, 2024, 22, 136-136. [28] M. Noor, New Approximation schemes for general variational inequalities Journal of Mathematical Analysis and Applications, 2000, 251(1), 217-229. [29] Z. Opial, Weak convergence of the sequence of successive approximations for nonexpansive mappings Bulletin of the American Mathematical Society, 1967, 73(4), 591-597. [30] K. Panigrahy and D. Mishra, A note on a faster fixed point iterative method the Journal of Analysis, 2023, 31(1), 831-854. [31] I. Podlubny, Fractional differential equations: An introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications Elsevier, 1998. [32] J. -P. Richard, Time-delay systems: An overview of some recent advances and open problems Automatica, 2003, 39(10), 1667-1694. [33] J. Schu, Weak and strong convergence to fixed points of asymptotically nonexpansive mappings Bulletin of Australian Mathematical Society, 1991, 43(1), 153-159. [34] H. Senter and W. Dotson Jr., Approximating fixed points of nonexpansive mappings Proceedings of the American Mathematical Society, 1974, 44(2), 375-380. [35] T. Suzuki, Fixed point theorems and convergence theorems for some generalized nonexpansive mappings Journal of Mathematical Analysis and Applications, 2008, 340(2), 1088-1095. [36] T. M. Tuyen and H. A. Hammad, Effect of shrinking projection and cq-methods on two inertial forward-backward algorithms for solving variational inclusion problems Rendiconti del Circolo Matematico di Palermo Series 2, 2021, 1-15. [37] K. Ullah and M. Arshad, Numerical reckoning fixed points for Suzuki's generalized nonexpansive mappings via new iteration process Filomat, 2018, 32(1), 187-196. [38] K. Ullah, N. Hussain, J. Ahmad and M. Arshad, Approximation of fixed points for a class of generalized nonexpansive mappings in Banach spaces Thai Journal of Mathematics, 2020, 18(3), 1149-1159. [39] G. Usurelu and M. Postolache, Algorithm for generalized hybrid operators with numerical analysis and applications Journal of Nonlinear and Variational Analysis, 2022, 6(3), 255-277. [40] F. -F. Wang, D. -Y. Chen, X. -G. Zhang and Y. Wu, The existence and uniqueness theorem of the solution to a class of nonlinear fractional order system with time delay Applied Mathematics Letters, 2016, 53, 45-51. [41] H. Ye, Y. Ding and J. Gao, The existence of a positive solution of d α [x(t)- x(0)] = x(t)f(t, xt), Positivity, 2007, 11(2), 341-350. [42] T. -M. Yu, A. A. Shahid, K. Shabbir, et al., An iteration process for a general class of contractive-like operators: Convergence, stability and polynomiography AIMS Mathematics, 2021, 6(7), 6699-6714. -
-
-
Figure 2.
Graphical analysis of iterates of iteration processes corresponding to Table 1.
-
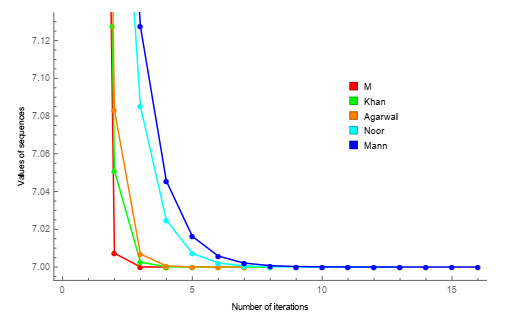
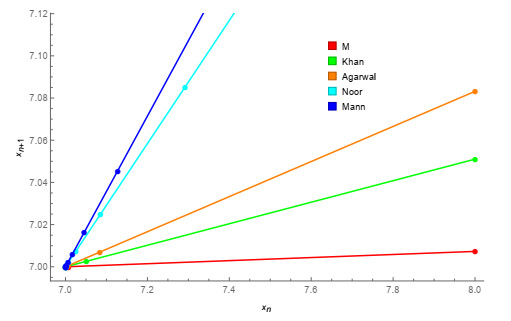
Figure 1.
Convergence behavior of M (1.7), Khan (1.4), Agarwal (1.5), Noor (1.6), and Mann (1.3) iteration processes corresponding to Table 1.
-
Figure 3.
Color map used in the examples.
-
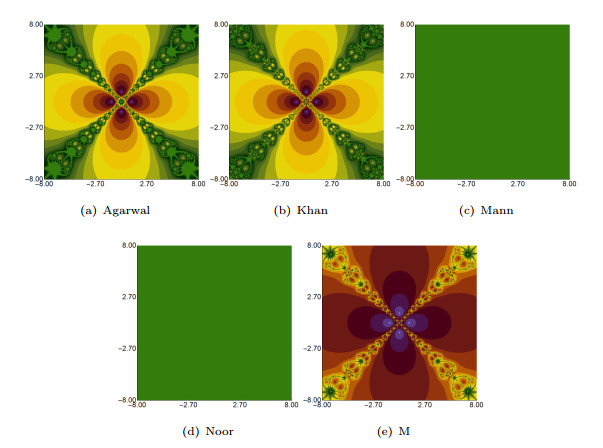
Figure 4.
Polynomiographs generated by various iteration processes with parameters
$ \alpha = \beta = \gamma = 0.03 $ -
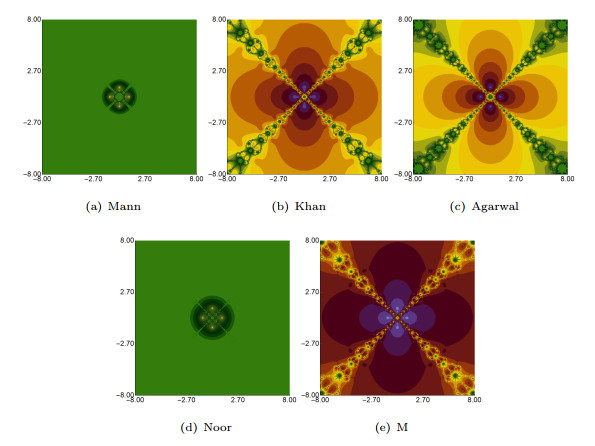
Figure 5.
Polynomiographs generated by various iteration processes with parameters
$ \alpha =\beta=\gamma= 0.4 $ -
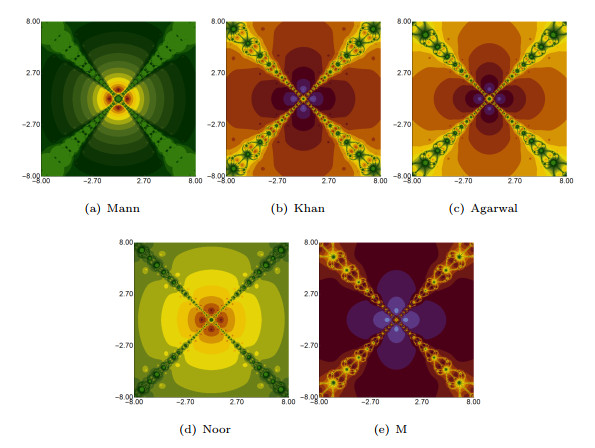
Figure 6.
Polynomiographs generated by various iteration processes with parameters
$ \alpha = \beta =\gamma = 0.7 $




 DownLoad:
DownLoad: