| Citation: | Yan Zhang, Bang-Sheng Han, Hong-Lei Wei, Yinghui Yang. SPATIAL DYNAMICS OF THE ADVECTIVE REACTION-DIFFUSION EQUATION ON FUNNEL-SHAPED DOMAINS[J]. Journal of Applied Analysis & Computation, 2025, 15(5): 2551-2569. doi: 10.11948/20240267 |
SPATIAL DYNAMICS OF THE ADVECTIVE REACTION-DIFFUSION EQUATION ON FUNNEL-SHAPED DOMAINS
-
Abstract
This paper is concerned with the entire solution of the advective reaction-diffusion equation with the bistable nonlinear reaction term on funnel-shaped domains. We focus on the well-posedness and long-time behavior of the entire solution. Because of the impact of advection, the previous super and sub-solutions are no longer applicable, so we study the existence of the entire solution behaving as a planar front by constructing appropriate super-solutions and sub-solutions. In addition, we show the uniqueness and Lyapunov stability of the entire solution. This is probably the first study of the advective reaction-diffusion on funnel-shaped domains.
-
Keywords:
- Reaction-diffusion equation /
- advective /
- bistable /
- entire solution
-

-
References
[1] H. Berestycki, The influence of advection on the propagation of fronts in reaction-diffusion equations, Nonlinear PDE's in Condensed Matter and Reactive Flows, Dordrecht: Springer Netherlands, 2002, 11–48. [2] H. Berestycki, J. Bouhours and G. Chapuisat, Front blocking and propagation in cylinders with varying cross section, Calc. Var. Partial Differential Equations, 2016, 55(3), 32 pp. [3] H. Berestycki and F. Hamel, Front propagation in periodic excitable media, Comm. Pure Appl. Math., 2002, 55(8), 949–1032. doi: 10.1002/cpa.3022 [4] H. Berestycki, F. Hamel and H. Matano, Bistable traveling waves around an obstacle, Comm. Pure Appl. Math., 2009, 62(6), 729–788. doi: 10.1002/cpa.20275 [5] H. Berestycki, F. Hamel and N. Nadirashvili, The speed of propagation for KPP type problems, I. Periodic Framework. J. Eur. Math. Soc., 2005, 7(2), 173–213. [6] H. Berestycki and L. Nirenberg, Travelling fronts in cylinders, Ann. Inst. H. Poincaré C Anal. Non Linéaire, 1992, 9(5), 497–572. doi: 10.1016/s0294-1449(16)30229-3 [7] J. Brasseur and J. Coville, Propagation phenomena with nonlocal diffusion in presence of an obstacle, J. Dynam. Differential Equations, 2023, 35(1), 237–301. doi: 10.1007/s10884-021-09988-y [8] Z. -H. Bu and Z. -C. Wang, Curved fronts of monostable reaction-advection-diffusion equations in space-time periodic media, Commun. Pure Appl. Anal., 2016, 15(1), 139–160. [9] G. Chapuisat and E. Grenier, Existence and nonexistence of traveling wave solutions for a bistable reaction-diffusion equation in an infinite cylinder whose diameter is suddenly increased, Comm. Partial Differential Equations, 2005, 30 (10–12), 1805–1816. [10] C. Cheng and Z. Zheng, Dynamics and spreading speed of a reaction-diffusion system with advection modeling West Nile virus, J. Math. Anal. Appl., 2021, 493(1), 24 pp. [11] S. Cox and G. Gottwald, A bistable reaction-diffusion system in a stretching flow, Phys. D, 2006, 216(2), 307–318. doi: 10.1016/j.physd.2006.03.007 [12] H. Guo, Transition fronts in unbounded domains with multiple branches, Calc. Var. Partial Differential Equations, 2020, 59(5), 40 pp. [13] H. Guo, F. Hamel and W. -J. Sheng, On the mean speed of bistable transition fronts in unbounded domains, J. Math. Pures Appl., 2020, 136(9), 92–157. [14] F. Hamel and M. Zhang, Reaction-diffusion fronts in funnel-shaped domains, Adv. Math., 2023, 412, 56 pp. [15] B. -S. Han, M. -X. Chang, H. Wei and Y. Yang, Curved fronts for a Belousov-Zhabotinskii system in exterior domains, J. Differential Equations, 2025, 416(2), 1660–1695. [16] B. -S. Han and D. Kong, Propagation dynamics of a nonlocal reaction-diffusion system, Discrete Contin. Dyn. Syst., 2023, 43(7), 2756–2780. doi: 10.3934/dcds.2023028 [17] J. Indekeu and R. Smets, Traveling wavefront solutions to nonlinear reaction-diffusion-convection equations, J. Phys. A., 2017, 50(31), 12 pp. [18] F. -J. Jia and Z. -C. Wang, Stability of entire solutions emanating from bistable planar traveling waves in exterior domains, Appl. Math. Lett., 2022, 132, 8 pp. [19] W. -T. Li, N. -W. Liu and Z. -C. Wang, Entire solutions in reaction-advection-diffusion equations in cylinders, J. Math. Pures Appl., 2008, 90(5), 492–504. doi: 10.1016/j.matpur.2008.07.002 [20] W. -T. Li, J. -B. Wang and L. Zhang, Entire solutions of nonlocal dispersal equations with monostable nonlinearity in space periodic habitats, J. Differential Equations, 2016, 261(4), 2472–2501. doi: 10.1016/j.jde.2016.05.006 [21] X. -M. Li and L. Li, Entire solutions of bistable reaction-diffusion systems in unbounded domain with multiple cylindrical branches, Discrete and Continuous Dynamical Systems, 2024, 29(9), 3856–3886. doi: 10.3934/dcdsb.2024026 [22] N. -W. Liu and W. -T. Li, Entire solutions in reaction-advection-diffusion equations with bistable nonlinearities in heterogeneous media, Sci. China Math., 2010, 53(7), 1775–1786. [23] N. -W. Liu, W. -T. Li and Z. -C. Wang, Entire solutions of reaction-advection-diffusion equations with bistable nonlinearity in cylinders, J. Differential Equations, 2009, 246(11), 4249–4267. [24] N. -W. Liu, W. -T. Li and Z. -C. Wang, Pulsating type entire solutions of monostable reaction-advection-diffusion equations in periodic excitable media, Nonlinear Anal., 2012, 75(4), 1869–1880. [25] Z. Ma and Z. -C. Wang, The trichotomy of solutions and the description of threshold solutions for periodic parabolic equations in cylinders, J. Dynam. Differential Equations, 2023, 35(4), 3665–3689. doi: 10.1007/s10884-021-10124-z?utm_content=meta [26] A. Pauthier, Entire solution in cylinder-like domains for a bistable reaction-diffusion equation, J. Dynam. Differential Equations, 2018, 30(3), 1273–1293. [27] J. Wang and W. Li, Pulsating waves and entire solutions for a spatially periodic nonlocal dispersal system with a quiescent stage, Sci. China Math., 2019, 62(12), 2505–2526. [28] J. Wang, X. Tong and Y. Song, Dynamics and pattern formation in a reaction-diffusion-advection mussel-algae model, Z. Angew. Math. Phys., 2022, 73(3), 21 pp. [29] Y. Wang, J. Shi and J. Wang, Persistence and extinction of population in reaction-diffusion-advection model with strong Allee effect growth, J. Math. Biol., 2019, 78(7), 2093–2140. [30] S. -L. Wu, L. Pang and S. Ruan, Propagation dynamics in periodic predator-prey systems with nonlocal dispersal, J. Math. Pures Appl., 2023, 170, 57–95. [31] S. -L. Wu, X. -Q. Zhao and C. -H. Hsu, Propagation dynamics for a time-periodic epidemic model in discrete media, J. Differential Equations, 2023, 374, 699–736. [32] T. Xiang, Global dynamics for a diffusive predator-prey model with prey-taxis and classical Lotka-Volterra kinetics, Nonlinear Anal. Real World Appl., 2018, 39, 278–299. [33] Z. Zhao, L. Li and Z. Feng, Traveling wavefronts for density-dependent diffusion reaction convection equation with time delay, Math. Methods Appl. Sci., 2024, 47(5), 3101–3114. [34] R. Zhou, S. -L. Wu and X. -X. Bao, Propagation dynamics for space-time periodic and degenerate systems with nonlocal dispersal and delay, Journal of Nonlinear Science, 2024, 34–69. -
-
-
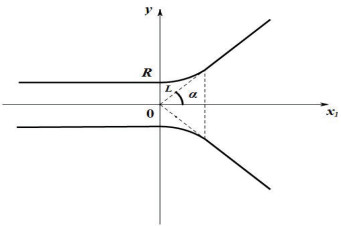
Figure 1.
The funnel-shaped domain
$ \Omega $




 DownLoad:
DownLoad: