| Citation: | D. Sh. Mohamed, M. A. Abdou, A. M. S. Mahdy. DYNAMICAL INVESTIGATION AND NUMERICAL MODELING OF A FRACTIONAL MIXED NONLINEAR PARTIAL INTEGRO-DIFFERENTIAL PROBLEM IN TIME AND SPACE[J]. Journal of Applied Analysis & Computation, 2024, 14(6): 3458-3479. doi: 10.11948/20240050 |
DYNAMICAL INVESTIGATION AND NUMERICAL MODELING OF A FRACTIONAL MIXED NONLINEAR PARTIAL INTEGRO-DIFFERENTIAL PROBLEM IN TIME AND SPACE
-
Abstract
In the current study, a novel and effective method for solving the nonlinear fractional mixed partial integro-differential equation (NfrPIo-DE) based on a continuous kernel is presented and discussed. The NfrPIo-DE is transformed into the nonlinear Fredholm integral equation (NFIE) through the utilization of the separation of variables. The NFIE reduction was then transformed into a system of nonlinear algebraic equations (SNAE) with the application of Chebyshev polynomials of the sixth type (CP6K). By utilizing the Banach fixed point theorem, we can describe the existence of the solution of NfrPIo-DE as well as its uniqueness. Furthermore, the convergence and the stability of the reduced error have been described. Finally, a numerical example is presented to illustrate the theoretical results. The Maple 18 software is responsible for getting all of the computational outcomes.
-

-
References
[1] W. M. Abd-Elhameed and Y. H. Youssri, Sixth-kind Chebyshev spectral approach for solving fractional differential equations, International Journal of Nonlinear Sciences and Numerical Simulation, 2019, 20(2), 191–203. doi: 10.1515/ijnsns-2018-0118 [2] W. M. Abd-Elhameed and Y. H. Youssri, Neoteric formulas of the monic orthogonal Chebyshev polynomials of the sixth kind involving moments and linearization formulas, Advances in Difference Equations, 2021, 2021, 1–19. doi: 10.1186/s13662-020-03162-2 [3] M. A. Abdou and M. Basseem, Numerical treatments for solving nonlinear mixed integral equation, Alexandria Engineering Journal, 2016, 55, 3247-3251. doi: 10.1016/j.aej.2016.02.035 [4] M. A. Abdou and M. I. Youssef, A new model for solving three mixed integral equations with continuous and discontinuous kernels, Asian Research Journal of Mathematics, 2021, 1–13. [5] A. M. Al-Bugami, M. A. Abdou and A. M. S. Mahdy, Sixth kind Chebyshev and Bernoulli polynomial numerical methods for solving nonlinear mixed partial integro-differential equations with continuous kernels, Journal of Function Spaces, 2023, 2023, 1–14. [6] F. M. Alharbi, A. M. Zidan, M. Naeem, R. Shah and K. Nonlaopon, Numerical investigation of fractional-order differential equations via $\varphi$ Haar-Wavelet method, Journal of Function Spaces, 2021, 2021, 1–14. $\varphi$ Haar-Wavelet method" target="_blank">Google Scholar
[7] Sh. E. Alhazmi and M. A. Abdou, A physical phenomenon for the fractional nonlinear mixed integro-differential equation using a general discontinuous kernel, Fractal and Fractional, 2023, 7(173), 1–19. [8] Sh. E. Alhazmi, A. M. S. Mahdy, M. A. Abdou and D. Sh. Mohamed, Computational techniques for solving mixed (1+1) dimensional integral equations with strongly symmetric singular kernel, Symmetry, 2023, 15(6), 1284, 1–27. doi: 10.3390/sym15061284 [9] R. E. Alsulaiman, M. A. Abdou, E. M. Youssef and M. Taha, Solvability of a nonlinear integro-differential equation with fractional order using the Bernoulli matrix approach, AIMS Mathematics, 2023, 8(3), 7515–7534. doi: 10.3934/math.2023377 [10] A. G. Atta, E. W. M. Abd-Elhameed, E G. M. Moatimid and E Y. H. Youssri, Advanced shifted sixth kind Chebyshev tau approach for solving linear one-dimensional hyperbolic telegraph type problem, Mathematical Sciences, 2022, 1–15. [11] M. Basseem and A. Alalyani, On the solution of quadratic nonlinear integral equation with different singular kernels, Mathematical Problems in Engineering, 2020, 2020, 1–7. [12] M. M. Bekkouche, I. Mansouri and A. A. Azeb Ahmed, Numerical solution of fractional boundary value problem with Caputo-Fabrizio and its fractional integral, Journal of Applied Mathematics and Computing, 2022, 68, 4305–4316. doi: 10.1007/s12190-022-01708-z [13] D. Guo, V. Lakshmikantham and X. Liu, Nonlinear Integral Equations in Abstract Spaces, Springer Science and Business Media, Springer New York, NY, 2013, 373. [14] R. M. Hafez and Y. H. Youssri, Spectral Legendre-Chebyshev treatment of 2D linear and nonlinear mixed Volterra-Fredholm integral equation, Mathematical Sciences Letters, 2020, 9(2), 37–47. [15] S. Hamdan, N. Qatanani and A. Daraghmeh, Numerical techniques for solving linear Volterra fractional integral equation, Journal of Applied Mathematics, 2019, 2019, 1–9. [16] A. R. Jan, An asymptotic model for solving mixed integral equation in position and time, Journal of Mathematics, 2022, 2022, 1–11. [17] A. Khalouta, A new general integral transform for solving Caputo fractional-order differential equations, International Journal of Nonlinear Analysis and Applications, 2023, 14(1), 67–78. [18] A. M. S. Mahdy, M. A. Abdou and D. Sh. Mohamed, Computational methods for solving higher-order (1+1) dimensional mixed-difference integro-differential equations with variable coefficients, Mathematics, 2023, 11(9), 1–25. [19] A. M. S. Mahdy, M. A. Abdou and D. Sh. Mohamed, A computational technique for computing second-type mixed integral equations with singular kernels, Journal of Mathematics and Computer Sciences, 2024, 32(2), 137–151. [20] A. M. S. Mahdy, A. S. Nagdy, K. M. Hashem and D. S. Mohamed, A computational technique for solving three-dimensional mixed Volterra-Fredholm integral equations, Fractal and Fractional, 2023, 7(2), 1–14. [21] K. S. Miller and B. Ross, An Introduction to the Fractional Calculus and Fractional Differential Equations, John Wiley and Sons. New York. 1993. [22] M. Mohammad, A. Trounev and M. Alshbool, A novel numerical method for solving fractional diffusion-wave and nonlinear Fredholm and Volterra integral equations with zero absolute error, Axioms, 2021, 10(3), 1–16. [23] A. Panda and J. Mohapatra, Analysis of some semi-analytical methods for the solutions of a class of time-fractional partial integro-differential equations, International Journal of Applied and Computational Mathematics, 2024, 10(54), 1–20. [24] P. Polyanin and A. V. Manzhirov, Handbook of Integral Equations, Chapman and Hall/CRC, New York, 2008. [25] Kh. Sadri and H. Aminikhah, Chebyshev polynomials of sixth kind for solving nonlinear fractional PDEs with proportional delay and its convergence analysis, Journal of Function Spaces, 2022, 1–20. [26] S. G. Samko, A. A. Kilbas and O. I. Marcihev, Fractional Integrals and Derivatives, Theory and Applications, Gordon and Breach, Switzerland, Reading, 1993. [27] S. Yaghoubi, H. Aminikhah and K. Sadri, A new efficient method for solving system of weakly singular fractional integro-differential equations by shifted sixth kind Chebyshev polynomials, Journal of Mathematics, 2022, 2022, 1–18. [28] Y. H. Youssri and A. G. Atta, Fejér-quadrature collocation algorithm for solving fractional integro-differential equations via Fibonacci polynomials, Contemporary Mathematics, 2024, 5(1), 296–308. [29] Y. H. Youssri and R. M. Hafez, Chebyshev collocation treatment of Volterra-Fredholm integral equation with error analysis, Arabian Journal of Mathematics, 2020, 9, 471–480. -
-
-
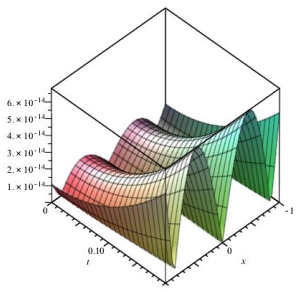
Figure 1.
Clarification of the error of absolute value of Example 8.1,
$ T=0.001, \alpha=0.8 $ -
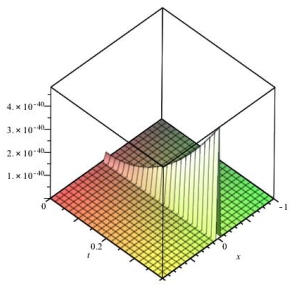
Figure 2.
Clarification of the error of absolute value Example 8.1 at,
$ T=0.2, \alpha=\frac{1}{5} $ -
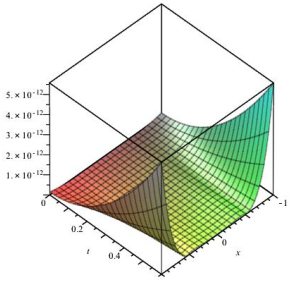
Figure 3.
At
$ T=0.4, \alpha=\frac{1}{2} $ -
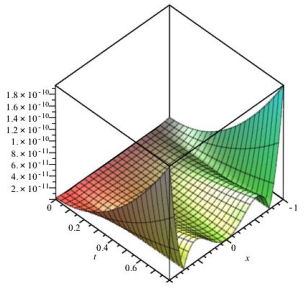
Figure 4.
At
$ T=0.6, \alpha=\frac{1}{2} $ -
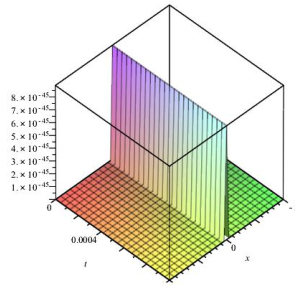
Figure 5.
At
$ T=0.8, \alpha=0.0004 $




 DownLoad:
DownLoad: