| Citation: |
Rui Qi, Caiqin Song. ITERATIVE ALGORITHMS FOR THE GENERALIZED DISCRETE-TIME PERIODIC SYLVESTER TRANSPOSE MATRIX EQUATIONS WITH APPLICATION IN THE PERIODIC STATE OBSERVER DESIGN OF LINEAR SYSTEMS[J]. Journal of Applied Analysis & Computation, 2025, 15(1): 286-315. doi: 10.11948/20240085
|
ITERATIVE ALGORITHMS FOR THE GENERALIZED DISCRETE-TIME PERIODIC SYLVESTER TRANSPOSE MATRIX EQUATIONS WITH APPLICATION IN THE PERIODIC STATE OBSERVER DESIGN OF LINEAR SYSTEMS
-
Abstract
In this work, four iterative algorithms are provided for solving generalized discrete-time periodic Sylvester transpose matrix equations. Based on the Jacobi iterative algorithm and hierarchical identification principle, the present work provides the full-row rank Jacobi gradient iterative (RRJGI) algorithm, the full-row rank accelerated Jacobi gradient iterative (RRAJGI) algorithm, the full-column rank Jacobi gradient iterative (CRJGI) algorithm and the full-column rank accelerated Jacobi gradient iterative (CRAJGI) algorithm. The convergence of the algorithms are proved, and it is concluded that the proposed iterative methods are convergent under certain conditions for arbitrary initial matrices. Numerical results show the feasibility of the proposed algorithms and its superiority compared with other algorithms. Finally, an application example for the periodic state observer design of linear systems is given.
-
-
References
[1] P. Benner, M. S. Hossain and T. Stykel, Low-rank iterative methods for periodic projected Lyapunov equations and their application in model reduction of periodic descriptor systems, Numerical Algorithms, 2012, 67(3), 669–690. [2] N. Boonruangkan and P. Chansangiam, Convergence analysis of a gradient iterative algorithm with optimal convergence factor for a generalized Sylvester-transpose matrix equation, AIMS Math., 2021, 6(8), 8477–8496. doi: 10.3934/math.2021492 [3] G. B. Cai and C. H. Hu, Solving periodic lyapunov matrix equations via finite steps iteration, IET Control Theory Appl., 2012, 6(13), 2111–2119. doi: 10.1049/iet-cta.2011.0560 [4] Z. B. Chen and X. S. Chen, Conjugate gradient-based iterative algorithm for solving generalized periodic coupled Sylvester matrix equations, Journal of the Franklin Institute, 2022, 359(17), 9925–9951. doi: 10.1016/j.jfranklin.2022.09.049 [5] K. W. Chu, H. Y. Fan and W. W. Lin, Projected generalized discrete-time periodic Lyapunov equations and balanced realization of periodic descriptor systems, SIAM Journal on Matrix Analysis and Applications, 2007, 29(3), 982–1006. doi: 10.1137/040606715 [6] F. Ding and H. M. Zhang, Gradient-based iterative algorithm for a class of the coupled matrix equations related to control systems, IET Control Theory Appl., 2014, 8(15), 1588–1595. doi: 10.1049/iet-cta.2013.1044 [7] M. Hajarian, Convergence analysis of the MCGNR algorithm for the least squares solution group of discrete-time periodic coupled matrix equations, Transactions of the Institute of Measurement and Control, 2017, 39(1), 29–42. doi: 10.1177/0142331215600253 [8] M. Hajarian, Extending LSQR methods to solve the generalized Sylvester-transpose and periodic Sylvester matrix equations, Mathematical Methods in the Applied Sciences, 2014, 37(13), 2017–2028. doi: 10.1002/mma.2955 [9] M. Hajarian, Matrix form of biconjugate residual algorithm to solve the discrete-time periodic sylvester matrix equations, Asian Journal of Control, 2018, 20(1), 49–56. doi: 10.1002/asjc.1528 [10] M. Hajarian, Reflexive periodic solutions of general periodic matrix equations, Mathematical Methods in the Applied Sciences, 2019, 42(10), 3527–3548. doi: 10.1002/mma.5596 [11] M. Hajarian, Solving the general Sylvester discrete-time periodic matrix equations via the gradient based iterative method, Appl. Math. Lett., 2016. DOI: 10.1016/j.aml.2015.08.017. [12] Z. H. He, Pure PSVD approach to Sylvester-type quaternion matrix equations, Electronic Journal of Linear Algebra, 2019. DOI: 10.13001/1081-3810.3917. [13] Z. H. He, Some new results on a system of Sylvester-type quaternion matrix equations, Linear and Multilinear Algebra, 2021, 69(16), 3069–3091. doi: 10.1080/03081087.2019.1704213 [14] Z. H. He, C. Navasca and X. X. Wang, Decomposition for a quaternion tensor triplet with applications, Advances in Applied Clifford Algebras, 2022. DOI: 10.1007/s00006-021-01195-8. [15] Z. H. He, W. L. Qin, J. Tian, X. X. Wang and Y. Zhang, A new Sylvester-type quaternion matrix equation model for color image data transmission, Computational and Applied Mathematics, 2024. DOI: 10.1007/s40314-024-02732-4. [16] Z. H. He and Q. W. Wang, A system of periodic discrete-time coupled sylvester quaternion matrix equations, Algebra Coll., 2017, 24(1), 169–180. doi: 10.1142/S1005386717000104 [17] Z. H. He, X. X. Wang and Y. F. Zhao, Eigenvalues of quaternion tensors with applications to color video processing, Journal of Scientific Computing, 2023. DOI: 10.1007/s10915-022-02058-5. [18] Z. H. He, X. N. Zhang and X. J. Chen, Unitary Diagonalization of the Generalized Complementary Covariance Quaternion Matrices with Application in Signal Processing, Mathematics, 2023. DOI: 10.3390/math11234840. [19] B. H. Huang and C. F. Ma, Finite iterative algorithm for the symmetric periodic least squares solutions of a class of periodic sylvester matrix equations, Numer. Algor., 2019. DOI: 10.1007/s11075-018-0553-8. [20] A. Kittisopaporn and P. Chansangiam, Approximated least-squares solutions of a generalized Sylvester-transpose matrix equation via gradient-descent iterative algorithm, Advances in Difference Equations, 2021. DOI: 10.1186/s13662-021-03427-4. [21] S. H. Li and C. F. Ma, Factor gradient iterative algorithm for solving a class of discrete periodic Sylvester matrix equations, Journal of the Franklin Institute, 2022, 359(17), 9952–9970. doi: 10.1016/j.jfranklin.2022.09.041 [22] Z. Y. Li, Y. Wang, B. Zhou and G. R. Duan, Least squares solution with the minimum-norm to general matrix equations via iteration, Applied Mathematics and Computation, 2010, 215(10), 3547–3562. doi: 10.1016/j.amc.2009.10.052 [23] L. L. Lv and L. Zhang, On the periodic Sylvester equations and their applications in periodic Luenberger observers design, Journal of the Franklin Institute, 2016, 353(5), 1005–1018. doi: 10.1016/j.jfranklin.2014.09.011 [24] L. L. Lv, Z. Zhang, L. Zhang and X. X. Liu, Gradient based approach for generalized discrete-time periodic coupled Sylvester matrix equations, Journal of the Franklin Institute, 2018, 355(15), 7691–7705. doi: 10.1016/j.jfranklin.2018.07.045 [25] C. F. Ma and T. X. Yan, A finite iterative algorithm for the general discrete-time periodic Sylvester matrix equations, Journal of the Franklin Institute, 2022, 359(9), 4410–4432. doi: 10.1016/j.jfranklin.2022.03.047 [26] X. P. Sheng, A relaxed gradient based algorithm for solving generalized coupled sylvester matrix equations, J. Franklin Inst., 2018, 355(10), 4282–4297. doi: 10.1016/j.jfranklin.2018.04.008 [27] K. Tansri and P. Chansangiam, Conjugate Gradient Algorithm for Least-Squares Solutions of a Generalized Sylvester-Transpose Matrix Equation, Symmetry, 2022. DOI: 10.3390/sym14091868. [28] A. Varga, On computing minimal realizations of periodic descriptor systems, IFAC Proceedings Volumes, 2007, 40(14), 175–180. doi: 10.3182/20070829-3-RU-4912.00030 [29] W. L. Wang and C. Q. Song, Iterative algorithms for discrete-time periodic Sylvester matrix equations and its application in antilinear periodic system, Applied Numerical Mathematics, 2021. DOI: 10.1016/j.apnum.2021.06.006. [30] Y. J. Xie and C. F. Ma, The accelerated gradient based iterative algorithm for solving a class of generalized Sylvester-transpose matrix equation, Applied Mathematics and Computation, 2016. DOI: 10.1016/j.amc.2015.07.022. [31] H. M. Zhang and H. C. Yin, New proof of the gradient-based iterative algorithm for a complex conjugate and transpose matrix equation, J. Frankl. Inst., 2017, 354(16), 7585–7603. doi: 10.1016/j.jfranklin.2017.09.005 [32] B. Zhou, Solutions to linear bimatrix equations with applications to pole assignment of complex-valued linear systems, J. Franklin Inst., 2018, 355(15), 7246–7280. doi: 10.1016/j.jfranklin.2018.07.015 [33] B. Zhou and G. R. Duan, Periodic Lyapunov equation based approaches to the stabilization of continuous-time periodic linear systems, IEEE Transactions on Automatic Control, 2012, 57(8), 2139–2146. doi: 10.1109/TAC.2011.2181796 [34] B. Zhou, G. R. Duan and Z. L. Lin, A parametric periodic lyapunov equation with application in semi-global stabilization of discrete-time periodic systems subject to actuator saturation, Automatica, 2011, 47(2), 316–325. doi: 10.1016/j.automatica.2010.10.011 -
-
Figures(2) / Tables(2)
Export File
Citation
Rui Qi, Caiqin Song. ITERATIVE ALGORITHMS FOR THE GENERALIZED DISCRETE-TIME PERIODIC SYLVESTER TRANSPOSE MATRIX EQUATIONS WITH APPLICATION IN THE PERIODIC STATE OBSERVER DESIGN OF LINEAR SYSTEMS[J]. Journal of Applied Analysis & Computation, 2025, 15(1): 286-315. doi: 10.11948/20240085
Format
Content
DownLoad:
-
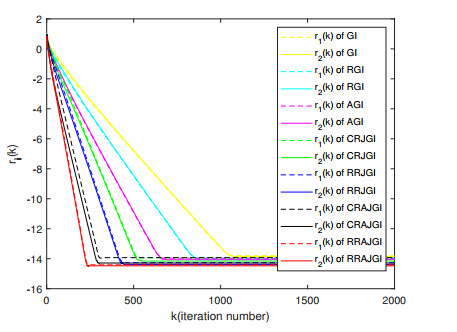
Figure 1.
Comparison of the convergence curves for Example 4.1.
-
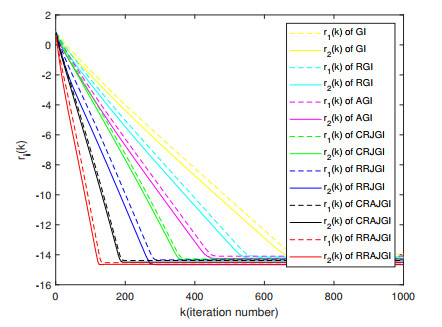
Figure 2.
Comparison of the convergence curves for Example 4.2.