| Citation: |
Changfeng Ma, Yuhong Wu, Yajun Xie. THE NEWTON-BASED MATRIX SPLITTING ITERATIVE METHOD FOR SOLVING GENERALIZED ABSOLUTE VALUE EQUATION WITH NONLINEAR TERM[J]. Journal of Applied Analysis & Computation, 2025, 15(2): 896-914. doi: 10.11948/20240198
|
THE NEWTON-BASED MATRIX SPLITTING ITERATIVE METHOD FOR SOLVING GENERALIZED ABSOLUTE VALUE EQUATION WITH NONLINEAR TERM
-
Abstract
A new Newton-based matrix splitting iterative method is proposed for solving generalized absolute value equation with nonlinear term. We give the global convergence of this method. Further some new convergence conditions are proposed when A = M - N is an H-compatible splitting. Numerical results indicate that the new Newton-based matrix splitting iterative method for solving generalized absolute value equation with nonlinear term is effective.
-
-
References
[1] L. Abdallah, M. Haddou and T. Migot, Solving absolute value equation using complementarity and smoothing functions, J. Comput. Appl. Math., 2018, 327, 196-207. doi: 10.1016/j.cam.2017.06.019 [2] Z. Z. Bai, On the convergence of the multisplitting methods for the linear complementarity problem, SIAM J. Matrix Anal. Appl., 1999, 21, 67-78. doi: 10.1137/S0895479897324032 [3] R. W. Cottle, J. S. Pang and R. E. Stone, The Linear Complementarity Problem, Academic, San Diego, 1992. [4] B. H. Huang and C. F. Ma, Convergent conditions of the generalized Newton method for absolute value equation over second order cones, Appl. Math. Lett., 2019, 92, 1-6. doi: 10.1016/j.aml.2018.12.021 [5] B. H. Huang and C. F. Ma, The modulus-based Levenberg-Marquardt method for solving linear complementarity problem, Numer. Math., 2019, 12, 154-168. [6] Y. F. Ke, The new iteration algorithm for absolute value equation, Appl. Math. Lett., 2020, 99, 105990. doi: 10.1016/j.aml.2019.07.021 [7] Y. F. Ke, Iterative Solution of Nonlinear Equations, Electronic Industry Press, Beijing, 2021. [8] C. F. Ma, L. H. Jiang and D. S. Wang, The convergence of a smoothing damped Gauss-Newton method for nonlinear complementarity problem, Nonlin. Anal. Real World Appl., 2009, 10, 2072-2087. doi: 10.1016/j.nonrwa.2008.03.013 [9] C. F. Ma, Y. F. Ke, J. Tang and B. G. Chen, Numerical Linear Algebra and Algorithms, National Defence Industry Press, Beijing, 2017. [10] O. L. Mangasarian, A generalized Newton method for absolute value equations, Optim. Lett., 2009, 3, 101-108. doi: 10.1007/s11590-008-0094-5 [11] O. L. Mangasarian, Absolute value programming, Comput. Optim. Appl., 2007, 36, 43-53. doi: 10.1007/s10589-006-0395-5 [12] O. L. Mangasarian and R. R. Meyer, Absolute value equations, Linear Algebra Appl., 2006, 419, 359-367. doi: 10.1016/j.laa.2006.05.004 [13] A. Mansoori and M. Erfanian, A dynamic model to solve the absolute value equations, J. Comput. Appl. Math., 2018, 333, 28-35. doi: 10.1016/j.cam.2017.09.032 [14] C. T. Nguyena, B. Saheyab, Y. L. Chang and J. S. Chen, Unified smoothing functions for absolute value equation associated with second-order cone, Appl. Numer. Math., 2019, 135, 206-227. doi: 10.1016/j.apnum.2018.08.019 [15] J. M. Ortega and W. C. Rheinboldt, Iterative Solution of Nonlinear Equations in Sevberal Variables, Academic Press, 1970. [16] J. Rohn, Systems of linear interval equations, Linear Alge. Appl., 1989, 126, 39-78. doi: 10.1016/0024-3795(89)90004-9 [17] J. Rohn, A theorem of the alternatives for the equation $Ax + B|x|= b$, Linear Multilinear Algebra, 2004, 52, 421-426. doi: 10.1080/0308108042000220686 [18] J. Rohn, V. Hooshyarbakhsh and R. Farhadsefat, An iterative method for solving absolute value equations and sufficient conditions for unique solvability, Optim. Lett., 2014, 8, 35-44. doi: 10.1007/s11590-012-0560-y [19] A. Wang, Y. Cao and J. X. Chen, Modified Newton-type iteration methods for generalized absolute value equations, J. Optim. Theo. Appl., 2019, 181, 216-230. doi: 10.1007/s10957-018-1439-6 [20] S. L. Wu, T. Z. Huang and X. L. Zhao, A modified SSOR iterative method for augmented systems, Comput. Appl. Math., 2009, 228, 424-433. doi: 10.1016/j.cam.2008.10.006 [21] S. F. Xu, Matrix Calculation in Cybernetics, Higher Education Press, Beijing, 2011. [22] C. C. Zhou, Y. Cao, Q. Q. Shen and Q. Shi, A modified Newton-based matrix splitting iteration method for generalized absolute value equations, J. Comput. Appl. Math., 2024, 442, 115747. doi: 10.1016/j.cam.2023.115747 [23] H. Y. Zhou, S. L. Wu and C. X. Li, Newton-basedd matrix splitting method for generalized absolute value equation, J. Comput. Appl. Math., 2021, 394, 360-375. -
-
Figures(6) / Tables(3)
Export File
Citation
Changfeng Ma, Yuhong Wu, Yajun Xie. THE NEWTON-BASED MATRIX SPLITTING ITERATIVE METHOD FOR SOLVING GENERALIZED ABSOLUTE VALUE EQUATION WITH NONLINEAR TERM[J]. Journal of Applied Analysis & Computation, 2025, 15(2): 896-914. doi: 10.11948/20240198
Format
Content
DownLoad:
-
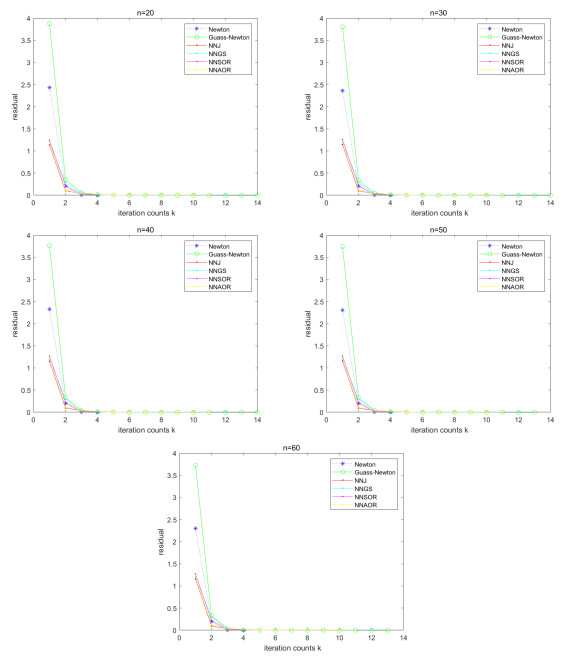
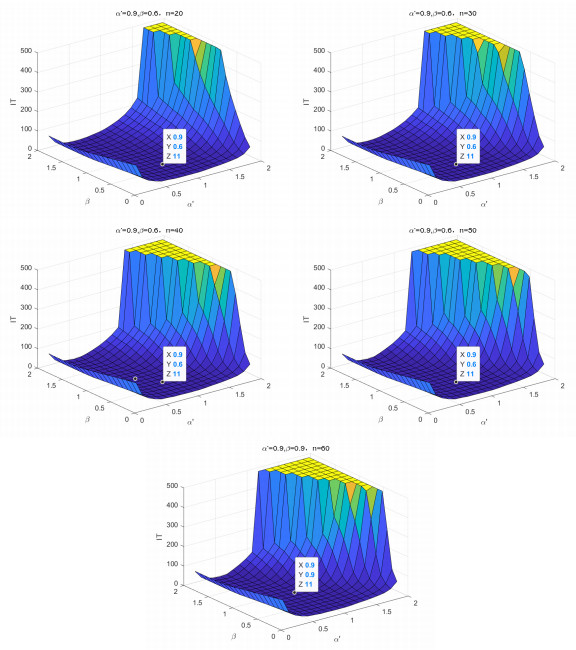
Figure 1.
Selection of optimal parameters
$ \alpha^{'}, \beta $ -
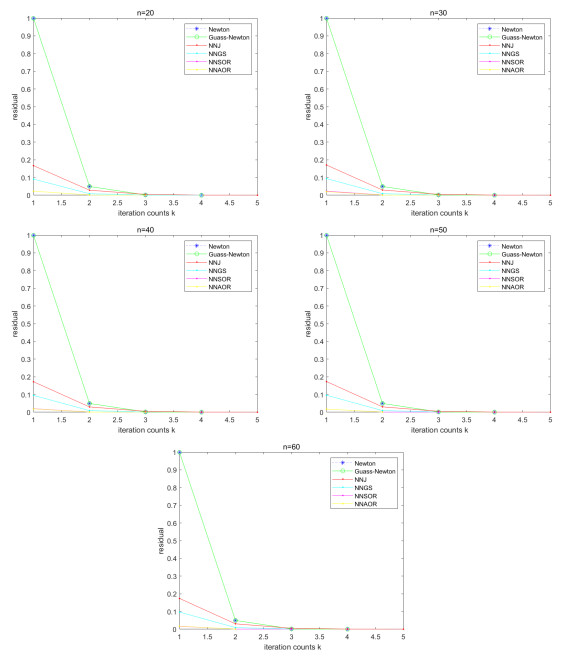
Figure 2.
Convergence effect for Example 5.1.
-
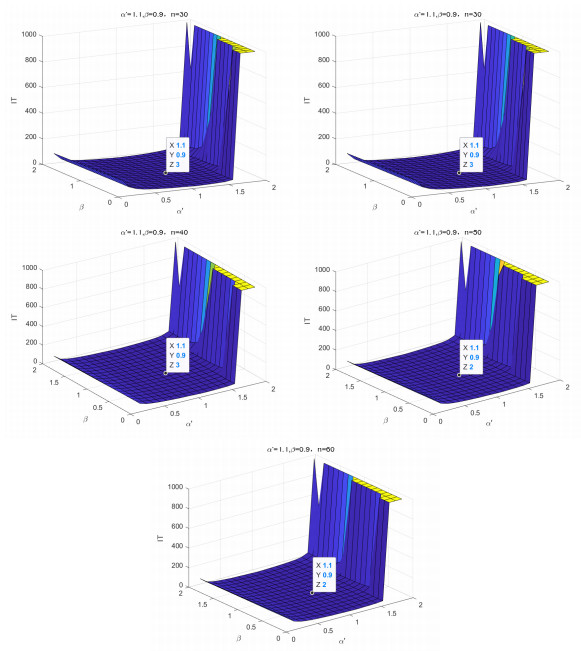
Figure 3.
Selection of optimal parameters
$ \alpha^{'}, \beta $ -
Figure 4.
Convergence effect for Example 5.2 (q=1;p=2).
-
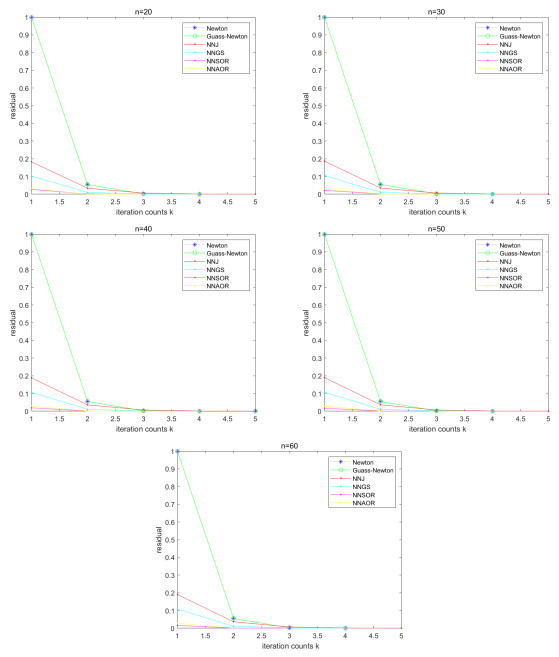
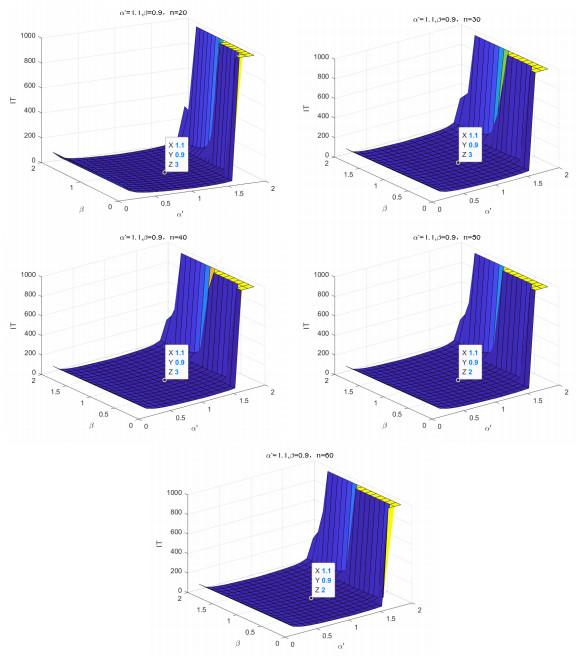
Figure 5.
Selection of optimal parameters
$ \alpha^{'}, \beta $ -
Figure 6.
Convergence effect for Example 5.2 (q=2;p=4).