| Citation: | Wenwen Xu, Xindong Li, Nana Song, Lu Yang, Xiqian Yuan. A TWO-GRID MULTIPOINT FLUX MIXED FINITE ELEMENT METHOD FOR NONLINEAR PARABOLIC PROBLEMS[J]. Journal of Applied Analysis & Computation, 2025, 15(3): 1310-1329. doi: 10.11948/20240209 |
A TWO-GRID MULTIPOINT FLUX MIXED FINITE ELEMENT METHOD FOR NONLINEAR PARABOLIC PROBLEMS
-
Abstract
This paper introduces a two-grid multipoint flux mixed finite element (MFMFE) method for solving nonlinear parabolic problems. The MFMFE method is advantageous due to its ability to decouple saddle point algebraic systems. The two-grid algorithm transforms nonlinear problems into smaller nonlinear systems on coarse grids and linear problems on fine grids, facilitating rapid decoupling of nonlinear equations. We present semi-discrete and fully discrete backward Euler schemes for the model problem. Theoretical results demonstrate the convergence order of velocity and pressure. A numerical example validates the effectiveness of the proposed algorithm, showing that the two-grid MFMFE method significantly reduces CPU running time compared to the standard MFMFE method.
-

-
References
[1] A. Bergam, C. Bernardi and Z. Mghazli, A posteriori analysis of the finite element discretization of some parabolic equations, Math. Comput., 2005, 74(251), 1117–1138. [2] F. Brezzi, J. Douglas, Jr. and L. D. Marini, Two families of mixed elements for second order elliptic problems, Numer. Math., 1985, 47, 217–235. doi: 10.1007/BF01389710 [3] F. Brezzi and M. Fortin, Mixed and Hybrid Finite Element Methods, Springer-Verlag, New York, 1991. [4] C. Chen and W. Liu, Two-grid finite volume element methods for semilinear parabolic problems, Appl. Numer. Math., 2010, 60(1–2), 10–18. [5] L. Chen and Y. Chen, Two-grid method for nonlinear reaction-diffusion equations by mixed finite element methods, J. Sci. Comput., 2011, 49(3), 383–401. doi: 10.1007/s10915-011-9469-3 [6] Y. Chen, Q. Li, Y. Wang and Y. Huang, Two-grid methods of finite element solutions for semi-linear elliptic interface problems, Numer. Algorithms, 2020, 84, 307–330. doi: 10.1007/s11075-019-00756-0 [7] P. G. Ciarlet, The Finite Element Method for Elliptic Problems, Society for Industrial and Applied Mathematics, 2002. [8] C. N. Dawson, M. F. Wheeler and C. S. Woodward, A two-grid finite difference scheme for nonlinear parabolic equations, SIAM J. Numer. Anal., 1998, 35(2), 435–452. doi: 10.1137/S0036142995293493 [9] S. Du, S. Sun and X. Xie, Residual-based a posteriori error estimation for multipoint flux mixed finite element methods, Numer. Math., 2016, 134(1), 197–222. doi: 10.1007/s00211-015-0770-1 [10] H. Egger and B. Radu, On a second-order multipoint flux mixed finite element methods on hybrid meshes, SIAM J. Numer. Anal., 2020, 58(3), 1822–1844. doi: 10.1137/19M1236862 [11] R. Eymard, T. Gallouït, R. Herbin and A. Michel, Convergence of a finite volume scheme for nonlinear degenerate parabolic equations, Numer. Math., 2002, 92(1), 41–82. doi: 10.1007/s002110100342 [12] S. M. F. Garcia, Improved error estimates for mixed finite‐element approximations for nonlinear parabolic equations: The continuous‐time case, Numer. Meth. Part. D. E., 1994, 10(2), 129–147. doi: 10.1002/num.1690100202 [13] Z. He, E. J. Chen, Z. Chen and T. Zhang, An online generalized multiscale approximation of the multipoint flux mixed finite element method, J. Comput. Appl. Math., 2024, 437, 115498. doi: 10.1016/j.cam.2023.115498 [14] C. Johnson and V. Thomée, Error estimates for some mixed finite element methods for parabolic type problems, RAIRO. Analyse Numérique, 1981, 15(1), 41–78. doi: 10.1051/m2an/1981150100411 [15] X. Li, M. Du and W. Xu, A multipoint flux mixed finite element method with mass-conservative characteristic finite element method for incompressible miscible displacement problem, Numer. Algorithms, 2023, 93(4), 1795–1810. doi: 10.1007/s11075-022-01489-3 [16] X. Li and H. Rui, A two-grid block-centered finite difference method for nonlinear non-Fickian flow model, Appl. Math. Comput., 2016, 281, 300–313. [17] W. Liu, H. Rui and X. Long, A two-grid algorithm for mixed finite element solution of nonlinear parabolic equations, Acta Math. Appl. Sin-E, 2007, 4, 635–643. [18] Y. Liu, C. W. Shu and M. Zhang, High order finite difference WENO schemes for nonlinear degenerate parabolic equations, SIAM J. Sci. Comput., 2011, 33(2), 939–965. doi: 10.1137/100791002 [19] H. Rui and W. Liu, A two-grid block-centered finite difference method for Darcy–Forchheimer flow in porous media, SIAM J. Numer. Anal., 2015, 53(4), 1941–1962. doi: 10.1137/14097954X [20] Z. Tan and Y. Zeng, Temporal second-order fully discrete two-grid methods for nonlinear time-fractional variable coefficient diffusion-wave equations, Appl. Math. Comput., 2024, 466, 128457. [21] V. Thomée, Galerkin Finite Element Methods for Parabolic Problems, Springer Verlag, Berlin, 2007. [22] M. F. Wheeler and I. Yotov, A cell-centered finite difference method for quadrilaterals, in Compatible Spatial Discretizations, IMA Vol. Math. Appl., 142, Springer-Verlag, New York, 2006, 189–208. [23] M. F. Wheeler and I. Yotov, A multipoint flux mixed finite element method, SIAM J. Numer. Anal., 2006, 44, 2082–2106. doi: 10.1137/050638473 [24] J. Xu, A novel two-grid method for semilinear elliptic equations, SIAM J. Sci. Comput., 1994, 15, 231–237. doi: 10.1137/0915016 [25] J. Xu, Two-grid discretization techniques for linear and nonlinear PDEs, SIAM J. Numer. Anal., 1996, 33, 1759–1777. doi: 10.1137/S0036142992232949 [26] W. Xu, D. Liang and H. Rui, A multipoint flux mixed finite element method for the compressible darcy-forchheimer models, Appl. Math. Comput., 2017, 315, 259–277. [27] W. Xu, D. Liang, H. Rui and X. Li, A multipoint flux mixed finite element method for Darcy–Forchheimer incompressible miscible displacement problem, J. Sci. Comput., 2020, 82, 1–20. doi: 10.1007/s10915-019-01102-1 -
-
-
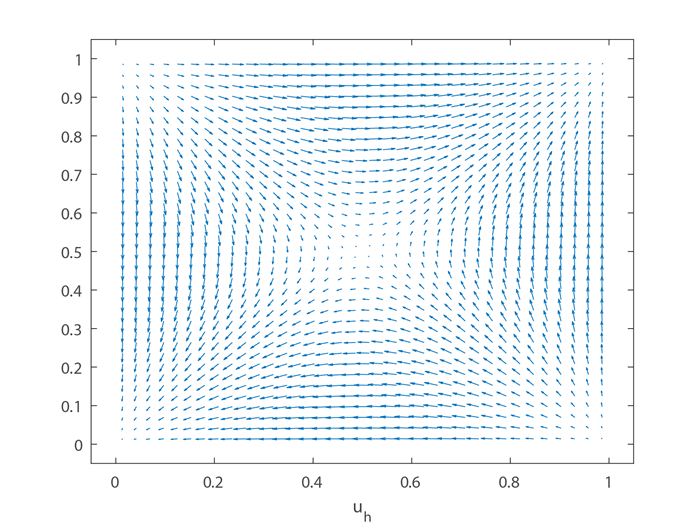
Figure 1.
The exact solution of velocity
$ \boldsymbol{u} $ -
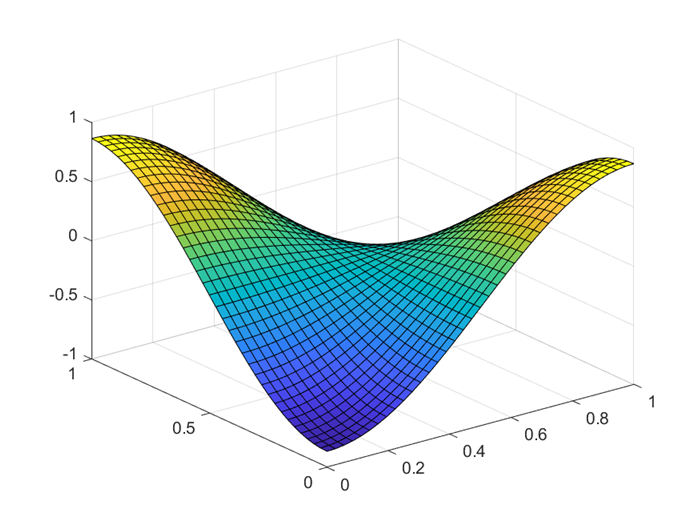
Figure 2.
The exact solution of pressure
$ p $ -
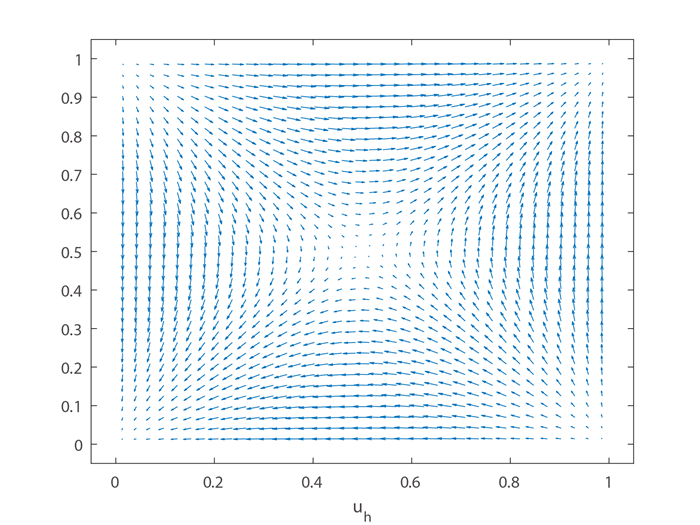
Figure 3.
The MFMFE solution of velocity
$ \boldsymbol{u}_h $ -
Figure 4.
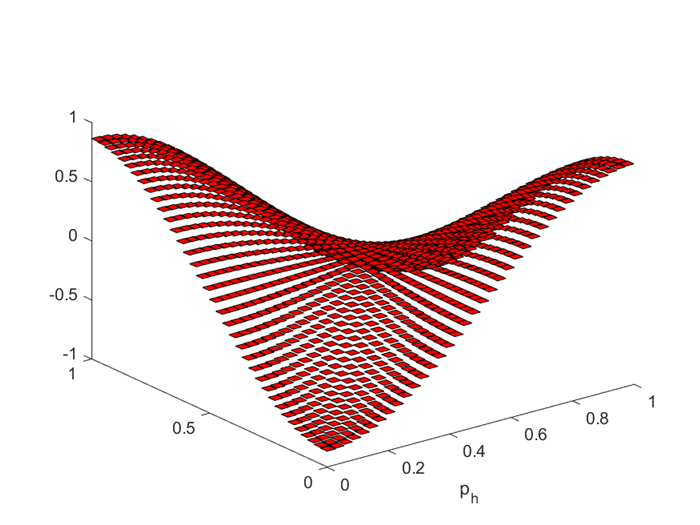
The MFMFE solution of pressure
$ p_h $ -
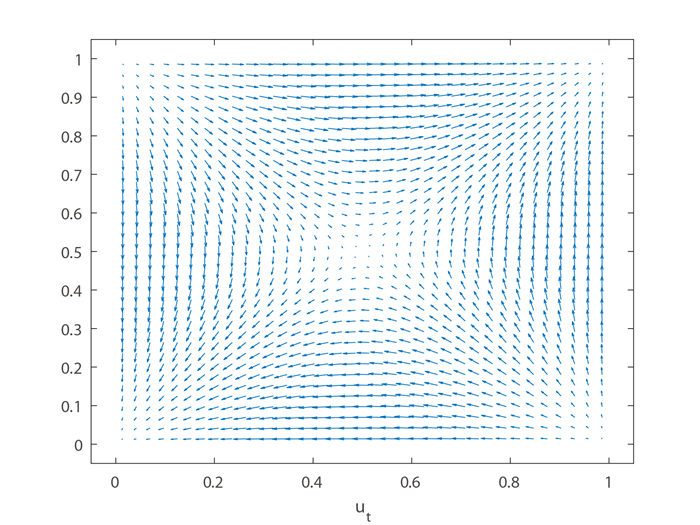
Figure 5.
The two-grid MFMFE solution of velocity
$ \boldsymbol{u}_h $ -
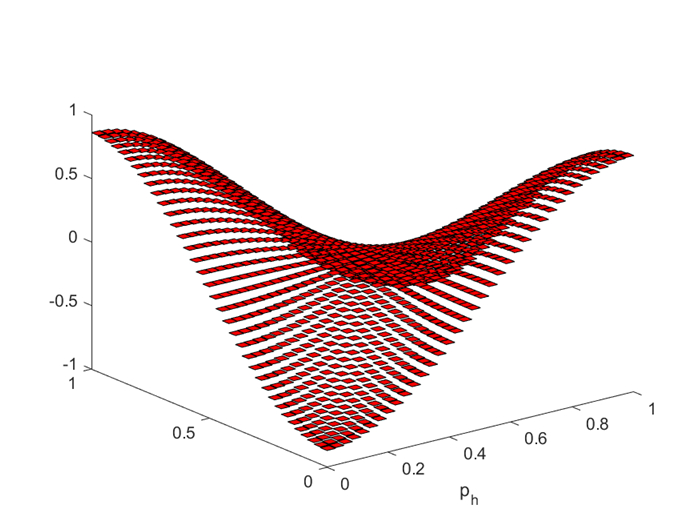
Figure 6.
The two-grid MFMFE solution of pressure
$ p_h $ -
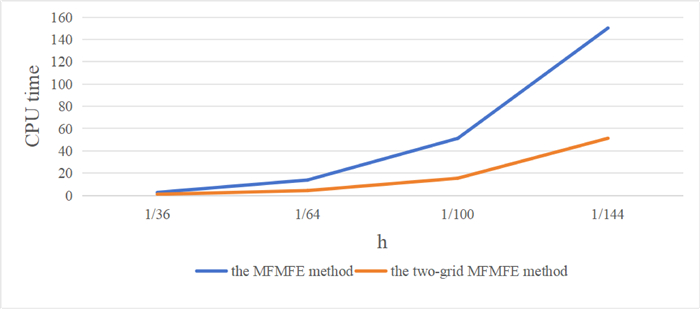
Figure 7.
The comparison of CPU time.




 DownLoad:
DownLoad: