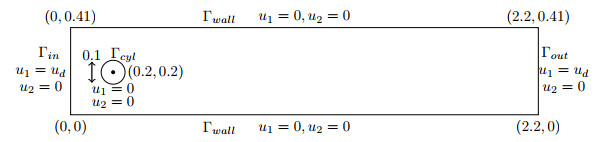| Citation: |
Bikram Bir, Deepjyoti Goswami. NUMERICAL ANALYSIS OF A GRAD-DIV STABILIZATION METHOD FOR THE OLDROYD MODEL OF ORDER ONE[J]. Journal of Applied Analysis & Computation, 2025, 15(3): 1330-1373. doi: 10.11948/20240226
|
NUMERICAL ANALYSIS OF A GRAD-DIV STABILIZATION METHOD FOR THE OLDROYD MODEL OF ORDER ONE
-
Abstract
This paper analyzes an inf-sup stable Galerkin mixed finite element method with a grad-div stabilization for the equation of the motion of the fluid arising in the Oldroyd model of order one. The main idea of the grad-div stabilization method is to add a stabilization term to the Galerkin approximation, which is very effective at a high Reynolds number. Optimal error bounds for the velocity in $ L^\infty( {\bf L}^2) $-norm and the pressure in $ L^2(L^2) $-norm are derived in the semidiscrete case with time remaining continuous. Then, a fully discrete scheme is analyzed by employing the backward Euler method, and optimal error estimates are derived. All these estimates are obtained with constants independent of the inverse of viscosity and for both the cases when the solution is as smooth as we want (has to satisfy nonlocal compatibility conditions) and when the solution is just smooth (compatibility conditions are no longer needed). Finally, we present some numerical results in support of our theoretical findings.
-
-
References
[1] M. Abbaszadeh and M. Dehghan, Investigation of the Oldroyd model as a generalized incompressible Navier–Stokes equation via the interpolating stabilized element free Galerkin technique, Applied Numerical Mathematics, 2020, 150, 274–294. doi: 10.1016/j.apnum.2019.08.025 [2] R. Adams, Sobolev Spaces, Press, New York, 1975. [3] N. Ahmed, On the grad-div stabilization for the steady Oseen and Navier-Stokes equations, Calcolo, 2017, 54, 471–501. doi: 10.1007/s10092-016-0194-z [4] D. N. Arnold, F. Brezzi and M. Fortin, A stable finite element for the Stokes equations, Calcolo, 1984, 21(4), 337–344. doi: 10.1007/BF02576171 [5] B. Bir and D. Goswami, On a three step two-grid finite element method for the Oldroyd model of order one, ZAMM-Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik, 2021, 101(11), e202000373. [6] B. Bir, D. Goswami and A. K. Pani, Backward Euler method for the equations of motion arising in Oldroyd model of order one with nonsmooth initial data, IMA Journal of Numerical Analysis, 2022, 42(4), 3529–3570. doi: 10.1093/imanum/drab072 [7] B. Bir, D. Goswami and A. K. Pani, Finite element penalty method for the Oldroyd model of order one with non-smooth initial data, Computational Methods in Applied Mathematics, 2022, 22(2), 297–325. doi: 10.1515/cmam-2022-0012 [8] D. Boffi, F. Brezzi and M. Fortin, Mixed Finite Element Methods and Applications, 44, Springer, 2013. [9] M. Braack and E. Burman, Local projection stabilization for the Oseen problem and its interpretation as a variational multiscale method, SIAM Journal on Numerical Analysis, 2006, 43(6), 2544–2566. doi: 10.1137/050631227 [10] S. C. Brenner, The Mathematical Theory of Finite Element Methods, Springer, 2008. [11] F. Brezzi and A. Russo, Choosing bubbles for advection-diffusion problems, Mathematical Models and Methods in Applied Sciences, 1994, 4(04), 571–587. doi: 10.1142/S0218202594000327 [12] A. N. Brooks and T. J. Hughes, Streamline upwind/Petrov-Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier-Stokes equations, Computer Methods in Applied Mechanics and Engineering, 1982, 32(1–3), 199–259. doi: 10.1016/0045-7825(82)90071-8 [13] E. Burman and P. Hansbo, Edge stabilization for Galerkin approximations of convection–diffusion–reaction problems, Computer Methods in Applied Mechanics and Engineering, 2004, 193(15–16), 1437–1453. doi: 10.1016/j.cma.2003.12.032 [14] P. G. Ciarlet, The Finite Element Method for Elliptic Problems, SIAM, 2002. [15] H. Dallmann, D. Arndt and G. Lube, Local projection stabilization for the Oseen problem, IMA Journal of Numerical Analysis, 2016, 36(2), 796–823. doi: 10.1093/imanum/drv032 [16] L. P. Franca and T. J. Hughes, Two classes of mixed finite element methods, Computer Methods in Applied Mechanics and Engineering, 1988, 69(1), 89–129. doi: 10.1016/0045-7825(88)90168-5 [17] J. de Frutos, B. García-Archilla, V. John and J. Novo, Grad-div stabilization for the evolutionary Oseen problem with inf-sup stable finite elements, Journal of Scientific Computing, 2016, 66(3), 991–1024. doi: 10.1007/s10915-015-0052-1 [18] J. de Frutos, B. García-Archilla, V. John and J. Novo, Analysis of the grad-div stabilization for the time-dependent Navier–Stokes equations with inf-sup stable finite elements, Advances in Computational Mathematics, 2018, 44, 195–225. doi: 10.1007/s10444-017-9540-1 [19] K. J. Galvin, A. Linke, L. G. Rebholz and N. E. Wilson, Stabilizing poor mass conservation in incompressible flow problems with large irrotational forcing and application to thermal convection, Computer Methods in Applied Mechanics and Engineering, 2012, 237, 166–176. [20] D. Goswami, P. D. Damázio, J. Y. Yuan and B. Bir, Two-grid finite element Galerkin approximation of equations of motion arising in Oldroyd fluids of order one with non-smooth initial data, Computational Mathematics and Mathematical Physics, 2023, 63(4), 659–686. doi: 10.1134/S0965542523040061 [21] D. Goswami and A. K. Pani, A priori error estimates for semidiscrete finite element approximations to the equations of motion arising in Oldroyd fluids of order one, International Journal of Numerical Analysis & Modeling, 2011, 8(2). [22] Y. Guo and Y. He, Crank–Nicolson extrapolation and finite element method for the Oldroyd fluid with the midpoint rule, Journal of Computational and Applied Mathematics, 2022, 415, 114453. doi: 10.1016/j.cam.2022.114453 [23] W.-W. Han, Y.-L. Jiang and Z. Miao, Numerical analysis of projection methods for the time-dependent Navier-Stokes equations with modular grad-div stabilization, Computers & Mathematics with Applications, 2023, 141, 145–158. [24] Y. He, Y. Lin, S. S. Shen, et al., Finite element approximation for the viscoelastic fluid motion problem, Journal of Computational and Applied Mathematics, 2003, 155(2), 201–222. doi: 10.1016/S0377-0427(02)00864-6 [25] F. Hecht, New development in FreeFem++, Journal of Numerical Mathematics, 2012, 20(3–4), 251–266. [26] J. G. Heywood and R. Rannacher, Finite element approximation of the nonstationary Navier–Stokes problem. Ⅰ. Regularity of solutions and second-order error estimates for spatial discretization, SIAM Journal on Numerical Analysis, 1982, 19(2), 275–311. doi: 10.1137/0719018 [27] J. G. Heywood and R. Rannacher, Finite-element approximation of the nonstationary Navier–Stokes problem, Part Ⅳ: Error analysis for second-order time discretization, SIAM Journal on Numerical Analysis, 1990, 27(2), 353–384. doi: 10.1137/0727022 [28] A. T. Hill and E. Süli, Approximation of the global attractor for the incompressible Navier–Stokes equations, IMA Journal of Numerical Analysis, 2000, 20(4), 633–667. doi: 10.1093/imanum/20.4.633 [29] E. W. Jenkins, V. John, A. Linke and L. G. Rebholz, On the parameter choice in grad-div stabilization for the Stokes equations, Advances in Computational Mathematics, 2014, 40, 491–516. doi: 10.1007/s10444-013-9316-1 [30] Y. Jiang, B. Zheng and Y. Shang, A parallel grad-div stabilized finite element algorithm for the Stokes equations with damping, Computers & Mathematics with Applications, 2023, 135, 171–192. [31] V. John, Reference values for drag and lift of a two-dimensional time-dependent flow around a cylinder, International Journal for Numerical Methods in Fluids, 2004, 44(7), 777–788. doi: 10.1002/fld.679 [32] V. John and A. Kindl, Numerical studies of finite element variational multiscale methods for turbulent flow simulations, Computer Methods in Applied Mechanics and Engineering, 2010, 199(13–16), 841–852. doi: 10.1016/j.cma.2009.01.010 [33] C. Liu and Z. Si, An incremental pressure correction finite element method for the time-dependent Oldroyd flows, Applied Mathematics and Computation, 2019, 351, 99–115. [34] G. Matthies, N. I. Ionkin, G. Lube and L. Röhe, Some remarks on residual-based stabilisation of inf-sup stable discretisations of the generalised Oseen problem, Computational Methods in Applied Mathematics, 2009, 9(4), 368–390. doi: 10.2478/cmam-2009-0024 [35] M. T. Mohan, Deterministic and stochastic equations of motion arising in Oldroyd fluids of order one: Existence, uniqueness, exponential stability and invariant measures, Stochastic Analysis and Applications, 2020, 38(1), 1–61. doi: 10.1080/07362994.2019.1646138 [36] J. Oldroyd, Non-Newtonian flow of liquids and solids, in Rheology, Elsevier, 1956, 653–682. [37] M. A. Olshanskii, A low order Galerkin finite element method for the Navier–Stokes equations of steady incompressible flow: A stabilization issue and iterative methods, Computer Methods in Applied Mechanics and Engineering, 2002, 191(47–48), 5515–5536. doi: 10.1016/S0045-7825(02)00513-3 [38] M. A. Olshanskii, G. Lube, T. Heister and J. Löwe, Grad–div stabilization and subgrid pressure models for the incompressible Navier–Stokes equations, Computer Methods in Applied Mechanics and Engineering, 2009, 198(49–52), 3975–3988. doi: 10.1016/j.cma.2009.09.005 [39] M. A. Olshanskii and A. Reusken, Grad-div stabilization for Stokes equations, Mathematics of Computation, 2004, 73(248), 1699–1718. [40] A. K. Pani and J. Y. Yuan, Semidiscrete finite element Galerkin approximations to the equations of motion arising in the Oldroyd model, IMA Journal of Numerical Analysis, 2005, 25(4), 750–782. doi: 10.1093/imanum/dri016 [41] A. K. Pani, J. Y. Yuan and P. D. Damázio, On a linearized backward Euler method for the equations of motion of Oldroyd fluids of order one, SIAM Journal on Numerical Analysis, 2006, 44(2), 804–825. [42] L. Röhe and G. Lube, Analysis of a variational multiscale method for Large–Eddy simulation and its application to homogeneous isotropic turbulence, Computer Methods in Applied Mechanics and Engineering, 2010, 199(37–40), 2331–2342. [43] Y. Shang, A two-level finite element method with grad-div stabilizations for the incompressible Navier–Stokes equations, Journal of Computational and Applied Mathematics, 2024, 446(17), 115865. [44] Y. Shang, J. Zhu and B. Zheng, A parallel finite element discretization algorithm based on grad-div stabilization for the Navier–Stokes equationss, Journal of Mathematical Fluid Mechanics, 2024, 26(3), 42. [45] K. Wang, Y. He and X. Feng, On error estimates of the penalty method for the viscoelastic flow problem Ⅰ: Time discretization, Applied Mathematical Modelling, 2010, 34(12), 4089–4105. [46] K. Wang, Y. He and X. Feng, On error estimates of the fully discrete penalty method for the viscoelastic flow problem, International Journal of Computer Mathematics, 2011, 88(10), 2199–2220. [47] K. Wang, Y. He and Y. Shang, Fully discrete finite element method for the viscoelastic fluid motion equations, Discrete & Continuous Dynamical Systems-B, 2010, 13(3), 665. [48] J. Wen, Z. Chen and Y. He, The analogue of grad-div stabilization in DG method for a coupled Stokes and Darcy problem, Computers & Mathematics with Applications, 2023, 149(3), 99–114. [49] Y. Yang, Y. Lei and Z. Si, Unconditional stability and error estimates of the modified characteristics fem for the time-dependent viscoelastic Oldroyd flows, Advances in Applied Mathematics and Mechanics, 2020, 13(2), 311–332. [50] T. Zhang and Y. Qian, Stability analysis of several first order schemes for the Oldroyd model with smooth and nonsmooth initial data, Numerical Methods for Partial Differential Equations, 2018, 34(6), 2180–2216. [51] T. Zhang, Y. Qian, T. Jiang and J. Yuan, Stability and convergence of the higher projection method for the time-dependent viscoelastic flow problem, Journal of Computational and Applied Mathematics, 2018, 338, 1–21. -
-
Figures(14) / Tables(4)
Export File
Citation
Bikram Bir, Deepjyoti Goswami. NUMERICAL ANALYSIS OF A GRAD-DIV STABILIZATION METHOD FOR THE OLDROYD MODEL OF ORDER ONE[J]. Journal of Applied Analysis & Computation, 2025, 15(3): 1330-1373. doi: 10.11948/20240226
Format
Content
DownLoad:
-
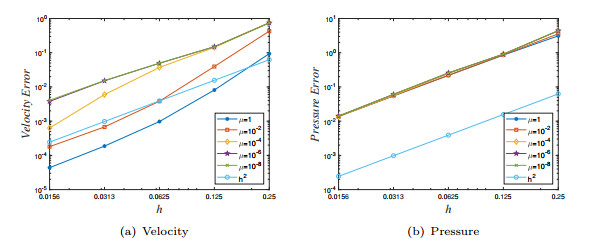
Figure 1.
Numerical errors in
$ {\bf L}^2 $ $ \rho=h^2 $ $ {\bf P}_1b, P_1 $ -
Figure 2.
Numerical errors in
$ {\bf L}^2 $ $ \rho=0.25 $ $ {\bf P}_2, P_1 $ -
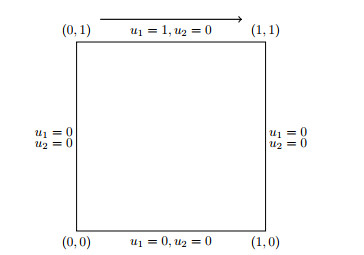
Figure 3.
Lid-driven cavity flow.
-
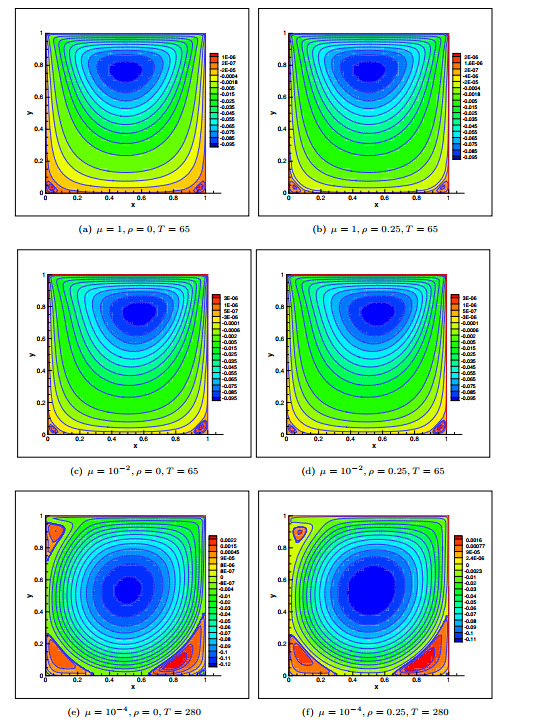
Figure 4.
Stream function for Example 5.2 for
$ h=1/64 $ -
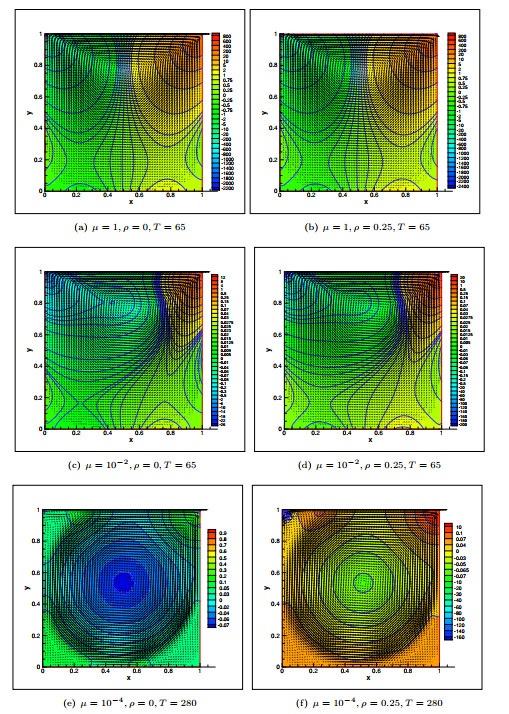
Figure 5.
Velocity vector and pressure contour for Example 5.2 for
$ h=1/64 $ -
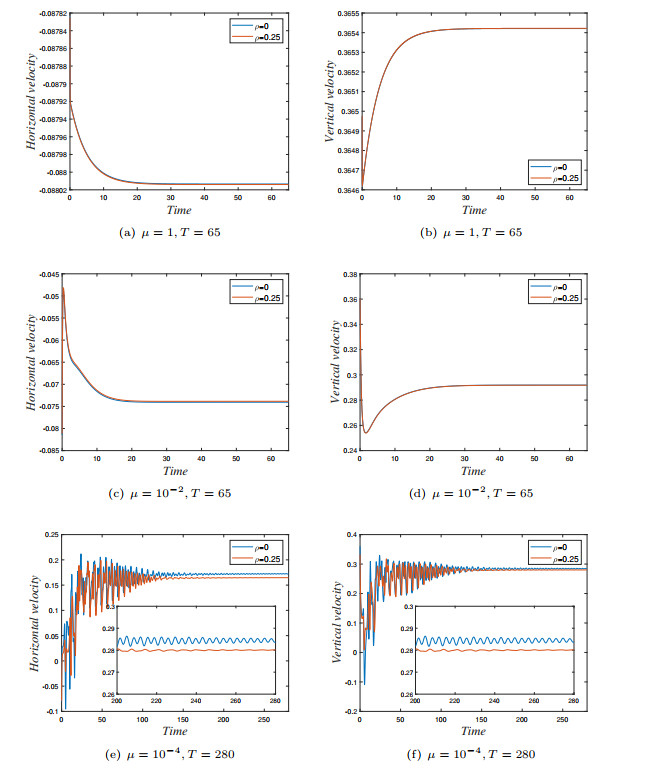
Figure 6.
Velocity profile at monitoring point (2/16, 13/16) for Example 5.2 for
$ h=1/64 $ -
Figure 7.
Domain
$ \Omega $ -
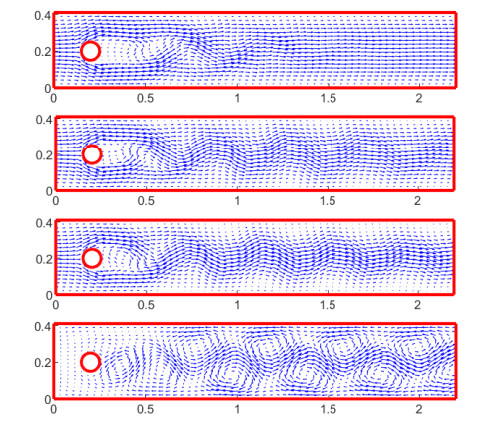
Figure 8.
Velocity field for Example 5.3 for
$ T=5, 6, 7, 8 $ -
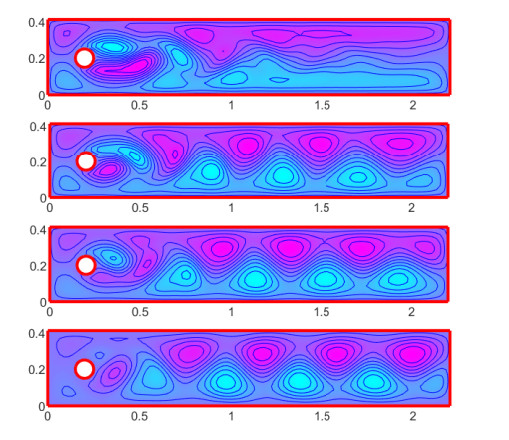
Figure 9.
Stream function for Example 5.3 for
$ T=5, 6, 7, 8 $ -
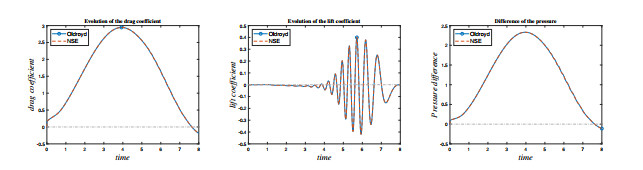
Figure 10.
Drag coefficient, lift coefficient, and pressure difference for Example 5.3.
-
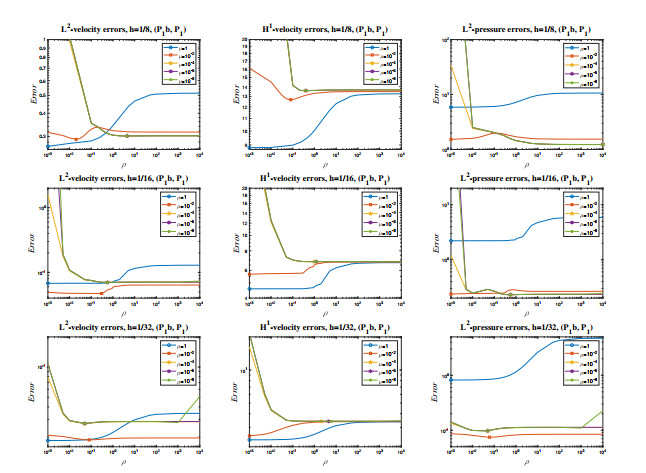
Figure 11.
Velocity and pressure errors vs stabilization parameter for
$ ({\bf P}_1b, P_1) $ -
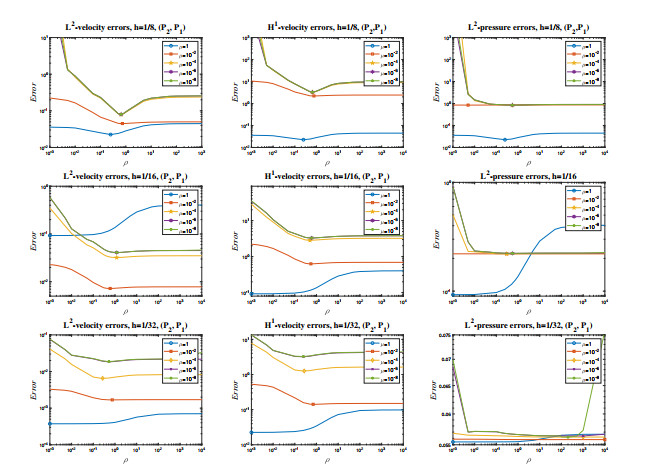
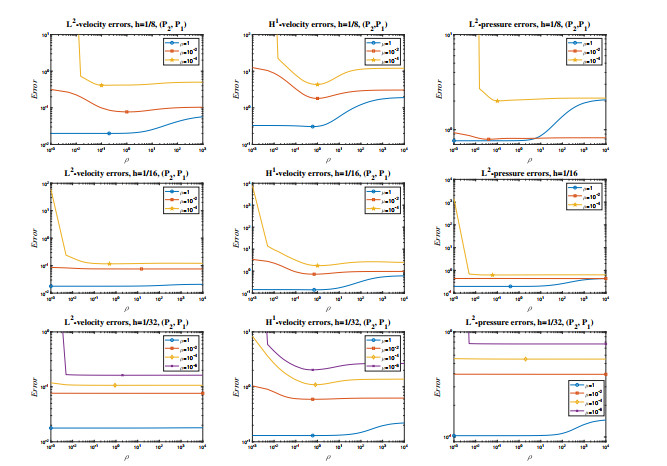
Figure 12.
Velocity and pressure errors vs stabilization parameter for
$ ({\bf P}_2, P_1) $ -
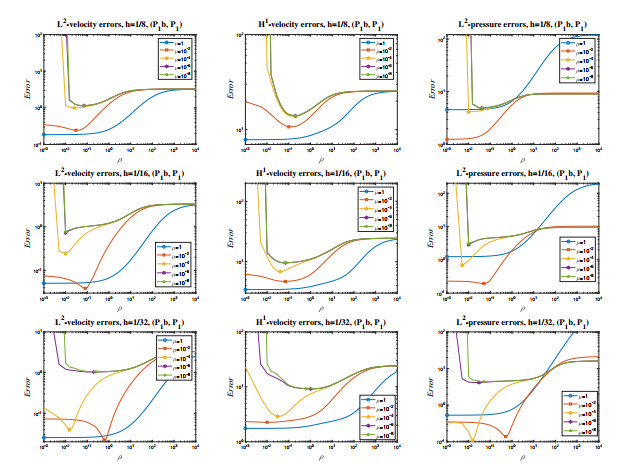
Figure 13.
Velocity and pressure errors vs stabilization parameter for
$ ({\bf P}_1b,P_1)$ -
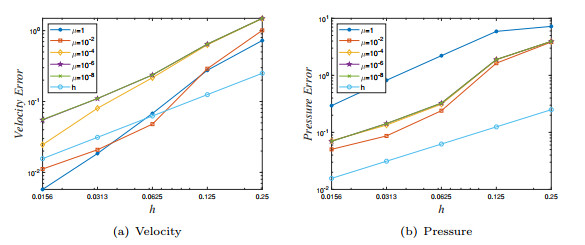
Figure 14.
Velocity and pressure errors vs stabilization parameter for
$ ({\bf P}_2,P_1)$