| Citation: |
Parvaiz Ahmad Naik, S. Naveen, V. Parthiban, Sania Qureshi, Marwan Alquran, Mehmet Senol. ADVANCING LOTKA-VOLTERRA SYSTEM SIMULATION WITH VARIABLE FRACTIONAL ORDER CAPUTO DERIVATIVE FOR ENHANCED DYNAMIC ANALYSIS[J]. Journal of Applied Analysis & Computation, 2025, 15(2): 1002-1019. doi: 10.11948/20240243
|
ADVANCING LOTKA-VOLTERRA SYSTEM SIMULATION WITH VARIABLE FRACTIONAL ORDER CAPUTO DERIVATIVE FOR ENHANCED DYNAMIC ANALYSIS
-
Abstract
This study investigates the application of the Caputo derivative with a variable fractional order to time-dependent models of Ordinary Differential Equations (ODEs), aiming to enhance the simulation accuracy of dynamic systems characterized by complex, nonlinear temporal behaviors. The proposed approach provides a more refined understanding and predictive capability for non-constant real-world phenomena, contributing to the development of advanced scientific and engineering solutions. The research centers on a variable-order Lotka-Volterra predator-prey model, employing the Arzelà-Ascoli and Schaefer fixed point theorems to establish the existence of solutions, and the Banach fixed point theorem to demonstrate their uniqueness. Numerical analyses are conducted to compare the proposed model with its integer-order, fractional-order, and variable-order counterparts, utilizing various time-varying and constant delay functions. The findings validate the efficacy of the proposed method in accurately modeling dynamic systems.
-
-
References
[1] H. Abdul, K. Adnan, G. Alhamzi and A. Saeed, A new solution of the nonlinear fractional logistic differential equations utilizing efficient techniques, AIP Advances, 2024, 14(035134). [2] H. Abdul, F. Mofarreh and K. Adnan, A fractional analysis of Zakharov–Kuznetsov equations with the Liouville–Caputo operator, Axioms, 2023, 12(6), 609. doi: 10.3390/axioms12060609 [3] H. G. Abdul, M. Houas, M. M. AlBaidani and D. Fathima, Coupled system of three sequential caputo fractional differential equations: Existence and stability analysis, Mathematical Methods in the Applied Sciences, 2023, 1–14. [4] N. Ahmed, M. Rani, S. S. Dragomir and A. Akgul, New exact solutions to space–time fractional telegraph equation with conformable derivative, International Journal of Modern Physics B, 2023, 2350275. [5] J. Alidousti and M. M. Ghahfarokhi, Stability and bifurcation for time delay fractional predator prey system by incorporating the dispersal of prey, Applied Mathematical Modelling, 2019, 72, 385–402. doi: 10.1016/j.apm.2019.03.029 [6] N. Bairagi and D. Adak, Switching from simple to complex dynamics in a predator–prey–parasite model: An interplay between infection rate and incubation delay, Mathematical Biosciences, 2016, 277, 1–14. doi: 10.1016/j.mbs.2016.03.014 [7] B. Bolaji, T. Onoja, C. Agbata, et al., Dynamical analysis of hiv-tb co-infection transmission model in the presence of treatment for tb, Bulletin of Biomathematics, 2024, 2(1), 21–56. [8] S. Boulaaras, M. Yavuz, Y. Alrashedi, et al., Modeling the co-dynamics of vector-borne infections with the application of optimal control theory, Discrete and Continuous Dynamical Systems-S, 2024, 17, 1–20. doi: 10.3934/dcdss.2023169 [9] R. Chinnathambi and F. A. Rihan, Stability of fractional-order Prey–Predator system with time-delay and monod–haldane functional response, Nonlinear Dynamics, 2018, 92(4), 1637–1648. doi: 10.1007/s11071-018-4151-z [10] J. Danane, M. Yavuz and M. Yıldız, Stochastic modeling of three-species Prey–Predator model driven by lévy jump with mixed holling-ii and beddington–deangelis functional responses, Fractal and Fractional, 2023, 7(10), 751. doi: 10.3390/fractalfract7100751 [11] R. M. Eide, A. L. Krause, N. T. Fadai and R. A. Van Gorder, Predator-prey-subsidy population dynamics on stepping-stone domains with dispersal delays, Journal of Theoretical Biology, 2018, 451, 19–34. doi: 10.1016/j.jtbi.2018.04.038 [12] Z. Eskandari, P. A. Naik and M. Yavuz, Dynamical behaviors of a discrete-time Prey-Predator model with harvesting effect on the predator, Journal of Applied Analysis and Computation, 2024, 14(1), 283–297. doi: 10.11948/20230212 [13] T. Faria, Stability and bifurcation for a delayed Predator–Prey model and the effect of diffusion, Journal of Mathematical Analysis and Applications, 2001, 254(2), 433–463. doi: 10.1006/jmaa.2000.7182 [14] M. Farman, A. Ahmad, A. Zehra, et al., Analysis and controllability of diabetes model for experimental data by using fractional operator, Mathematics and Computers in Simulation, 2023. [15] A. H. Ganie, S. Noor, M. Al Huwayz, et al., A new solution of the nonlinear numerical simulations for fractional hirota–satsuma coupled Korteweg–de vries systems, Open Physics, 2024. [16] M. Higazy, H. Hijaz, A. H. Ganie, et al., Theoretical analysis and computational modeling of nonlinear fractional-order-two predators model, Results in Physics, 2021, 17, 105139. [17] C. Huang, X. Song, B. Fang, et al., Modeling, analysis and bifurcation control of a delayed fractional-order Predator–Prey model, International Journal of Bifurcation and Chaos, 2018, 28(09), 1850117. [18] M. Izadi, A. El-Mesady and W. Adel, A novel touchard polynomial-based spectral matrix collocation method for solving the Lotka-Volterra competition system with diffusion, Mathematical Modelling and Numerical Simulation with Applications, 2024, 4(1), 37–65. doi: 10.53391/mmnsa.1408997 [19] I. Khan, R. Nawaz, A. H. Ali, et al., Comparative analysis of the fractional order Cahn-Allen equation, Partial Differential Equations in Applied Mathematics, 2023, 8, 100576. doi: 10.1016/j.padiff.2023.100576 [20] V. Lakshmikantham and A. S. Vatsala, Basic theory of fractional differential equations, Nonlinear Analysis: Theory, Methods & Applications, 2008, 69(8), 2677–2682. [21] Z. Li, W. Zhang, C. Huang, et al., Bifurcation for a fractional-order lotka-volterra predator-prey model with delay feedback control, AIMS Mathematics, 2021, 6(1), 675–687. doi: 10.3934/math.2021040 [22] R. M. May, Time-delay versus stability in population models with two and three trophic levels, Ecology, 1973, 54(2), 315–325. doi: 10.2307/1934339 [23] P. A. Naik, M. Amer, R. Ahmed, et al., Stability and bifurcation analysis of a discrete Predator-Prey system of ricker type with refuge effect, Mathematical Biosciences and Engineering, 2024, 21(3), 4554–4586. doi: 10.3934/mbe.2024201 [24] P. A. Naik, Z. Eskandari and H. E. Shahraki, Flip and generalized flip bifurcations of a two-dimensional discrete-time chemical model, Mathematical Modelling and Numerical Simulations with Applications (MMNSA), 2021, 1(2), 95–101. doi: 10.53391/mmnsa.2021.01.009 [25] P. A. Naik, Z. Eskandari, H. E. Shahkari and K. M. Owolabi, Bifurcation analysis of a discrete-time Prey-Predator model, Bulletin of Biomathematics, 2023, 1(2), 111–123. [26] P. A. Naik, Z. Eskandari, M. Yavuz and Z. Huang, Bifurcation results and chaos in a two-dimensional Predator-Prey model incorporating holling-type response function on the predator, Discrete and Continuous Dynamical Systems-S, 2024, 17(12), 1–18. [27] P. A. Naik, M. Yavuz, S. Qureshi, et al., Memory impacts in hepatitis c: A global analysis of a fractional-order model with an effective treatment, Computer Methods and Programs in Biomedicine, 2024, 254, 108306. doi: 10.1016/j.cmpb.2024.108306 [28] P. A. Naik, B. M. Yeolekar, S. Qureshi, et al., Modeling and analysis of the fractional-order epidemic model to investigate mutual influence in hiv/hcv co-infection, Nonlinear Dynamics, 2024, 112(13), 11679–11710. doi: 10.1007/s11071-024-09653-1 [29] S. Naveen and V. Parthiban, Qualitative analysis of variable-order fractional differential equations with constant delay, Mathematical Methods in the Applied Sciences, 2023, 1–12. [30] S. Naveen, V. Parthiban and M. I. Abbas, Qualitative analysis of rlc circuit described by hilfer derivative with numerical treatment using the lagrange polynomial method, Fractal and Fractional, 2023, 7(11). [31] S. Naveen, R. Srilekha, S. Suganya and V. Parthiban, Controllability of damped dynamical systems modelled by hilfer fractional derivatives, Journal of Taibah University for Science, 2022, 16(1), 1254–1263. doi: 10.1080/16583655.2022.2157188 [32] S. Paul, A. Mahata, S. Mukherjee, et al., Study of fractional order sir model with mh type treatment rate and its stability analysis, Bulletin of Biomathematics, 2024, 2(1), 85–113. [33] M. Peng, Z. Zhang and X. Wang, Hybrid control of hopf bifurcation in a Lotka-Volterra Predator-Prey model with two delays, Advances in Difference Equations, 2017, 2017(1), 1–20. doi: 10.1186/s13662-016-1057-2 [34] I. Podlubny, Fractional differential equations: An introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications, Elsevier, 1998. [35] M. Qayyum, E. Ahmad, S. T. Saeed, et al., Traveling wave solutions of generalized seventh-order time-fractional kdv models through he-laplace algorithm, Alexandria Engineering Journal, 2023, 70, 1–11. doi: 10.1016/j.aej.2023.02.007 [36] F. Rihan, S. Lakshmanan, A. Hashish, et al., Fractional-order delayed Predator–Prey systems with holling type-ii functional response, Nonlinear Dynamics, 2015, 80, 777–789. doi: 10.1007/s11071-015-1905-8 [37] R. Shi and L. Chen, Staged-structured Lotka–Volterra Predator–Prey models for pest management, Applied Mathematics and Computation, 2008, 203(1), 258–265. doi: 10.1016/j.amc.2008.04.032 [38] K. White, J. D. Murray and M. Lewis, Wolf-deer interactions: A mathematical model, Proceedings of the Royal Society of London. Series B: Biological Sciences, 1996, 263(1368), 299–305. doi: 10.1098/rspb.1996.0046 [39] X. -P. Yan and W. -T. Li, Hopf bifurcation and global periodic solutions in a delayed Predator–Prey system, Applied Mathematics and Computation, 2006, 177(1), 427–445. doi: 10.1016/j.amc.2005.11.020 [40] X. -P. Yan and C. -H. Zhang, Hopf bifurcation in a delayed lokta–volterra Predator–Prey system, Nonlinear Analysis: Real World Applications, 2008, 9(1), 114–127. doi: 10.1016/j.nonrwa.2006.09.007 [41] L. Zu, D. Jiang, D. O'Regan, et al., Ergodic property of a Lotka–Volterra Predator–Prey model with white noise higher order perturbation under regime switching, Applied Mathematics and Computation, 2018, 330, 93–102. doi: 10.1016/j.amc.2018.02.035 -
-
Figures(7)
Export File
Citation
Parvaiz Ahmad Naik, S. Naveen, V. Parthiban, Sania Qureshi, Marwan Alquran, Mehmet Senol. ADVANCING LOTKA-VOLTERRA SYSTEM SIMULATION WITH VARIABLE FRACTIONAL ORDER CAPUTO DERIVATIVE FOR ENHANCED DYNAMIC ANALYSIS[J]. Journal of Applied Analysis & Computation, 2025, 15(2): 1002-1019. doi: 10.11948/20240243
Format
Content
DownLoad:
-
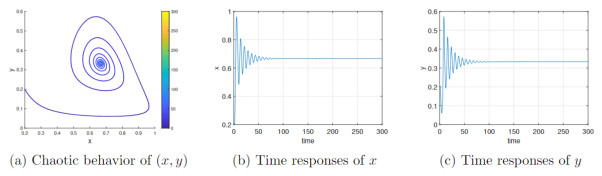
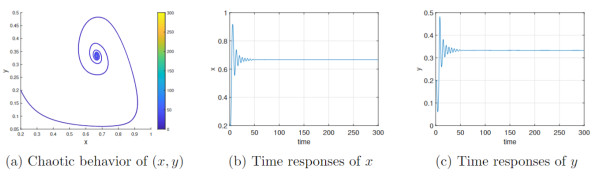
Figure 1.
Dynamical response of the integer-order version of the Lotka-Volterra predator-prey model with time-varying delay function
$ \tau(p)=\frac{80e^p}{1+e^p} $ -
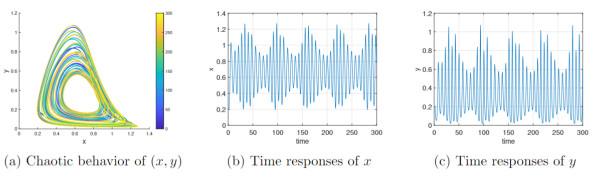
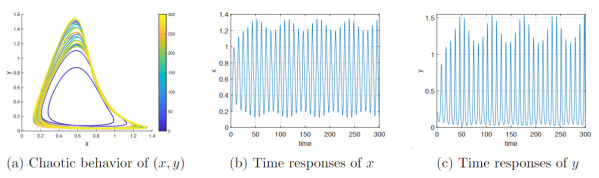
Figure 2.
Dynamical response of the fractional-order
$ (\vartheta = 0.95) $ $ \tau(p)=\frac{80e^p}{1+e^p} $ -
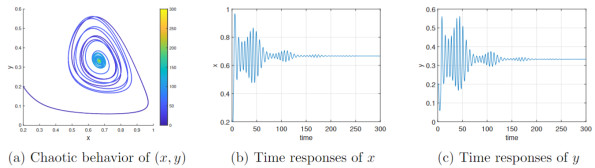
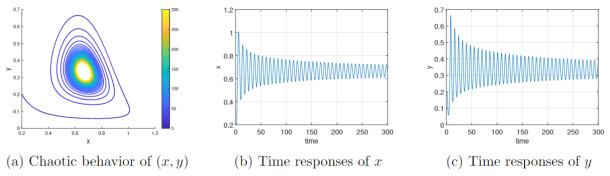
Figure 3.
Variable order constant delay with
$ \tau(p)=0.75 $ -
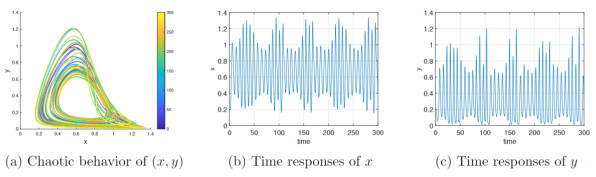
Figure 4.
Variable order constant delay
$ \tau(p)=0.60 $ -
Figure 5.
Variable order constant delay
$ \tau(p)=0.60 $ -
Figure 6.
Variable order constant delay
$ \tau(p)=0.60 $ -
Figure 7.
Variable order constant delay
$ \tau(p)=0.60 $